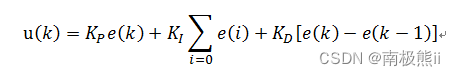PID详解汇总（持续更新）

大家好，欢迎来到IT知识分享网。

一、PID简介

        1、PID时间系数对PID本身的影响：

        这里的时间系统，一般指的是采样的时间，也就是PID控制的周期。在无人机当中一般采用10ms控制一次。

        一般来说采样周期越小，数字模拟越精确，控制效果越接近连续控制。对大多数算法，缩短采样周期可使控制回路性能改善，但采样周期缩短时，频繁的采样必然会占用较多的计算工作时间，同时也会增加计算机的计算负担。

        对于变化迅速的，采样周期应适当减小。对于多回路控制，采样周期应该适当延长，使得有足够的时间控制。

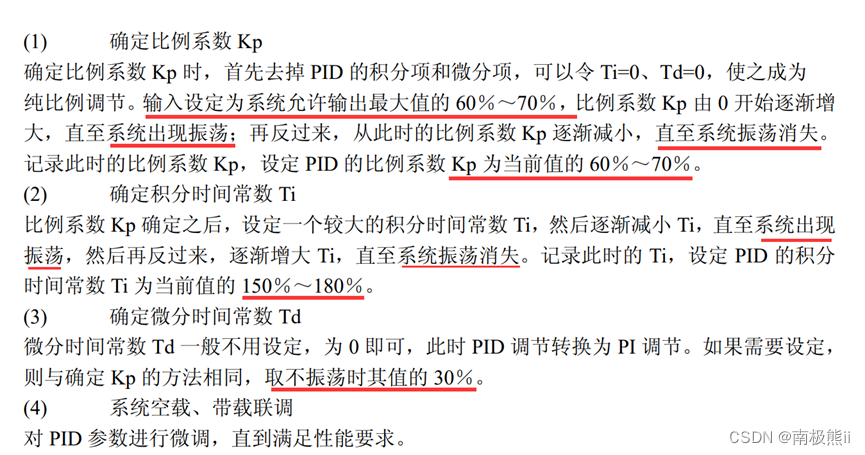
        2、PID参数

        比例环节：对偏差瞬间作出反应。偏差一旦产生控制器立即产生控制作用，使控制量向减少偏差的方向变化。控制作用的强弱取决于比例系数 ，比例系数越大，控制作用越强，则过渡过程越快，控制过程的静态偏差也就越小；但是也越容易产生振荡，破坏系统的稳定性。

        积分环节：虽然会消除静态误差，但也会降低系统的响应速度，增加系统的超调量。 

        微分环节：阻止偏差的变化。它是根据偏差的变化趋势（变化速度）进行控制。偏差变化的越快，微分控制器的输出就越大。微分作用的引入，将有助于减小超调量，克服振荡，使系统趋于稳定，特别对髙阶系统非常有利。 但微分的作用对输入信号的噪声很敏感，对那些噪声较大的系统一般不用微分，或在微分起作用之前先对输入信号进行滤波。

二、位置式PID

        优点：静态误差小，溢出的影响小。
        缺点：计算量很大，累积误差相对大，在系统出现错误的情况下，容易使系统失控，积分饱和。

        使用：一般需要结合输出限幅和积分限幅使用。积分限幅是避免积分失控的一种手段，也是为了加快调节时间，减少积分饱和的影响, 输出限幅是为了使系统输出不过度，也能够减少系统的调节时间，减少超调量。

        位置式PID适用于执行没有积分部件的对象。在控制系统中，这种控制量确定了执行机构的位置，例如在阀门控制中，这种算法的输出对应了阀门的位置(开度)。所以，将这种算法称为“位置算法”。

三、增量式PID

增量式PID

• 离散化后的公式：

        优点：溢出的影响小，在系统出现错误的情况下,影响相对较小（因为只与过去的三次误差有关）,运算量也相对较小。

        缺点：有静态误差（因为没有累积误差）。

        使用：位置式PID适用于执行有积分部件的对象。当执行机构需要的不是控制量的绝对值，而是控制量的增量(例如去驱动步进电动机)时，需要用PID的“增量算法”

四、两种针对积分的PID

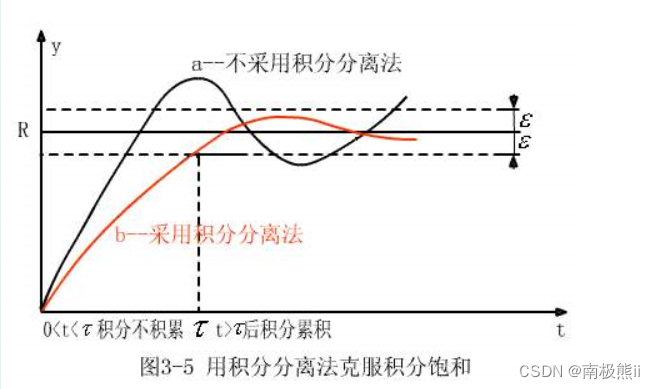
1、积分分离式PID：

积分分离式PID主要是针对位置式PID的积分，引入判断误差大小条件，是否使用积分项。

优点：
判定误差比较大的时候，取消积分项的，使用PD或者P控制，没有I的控制，这样，超调量和调节时间都会同时减少。当误差比较小的时候，引入积分项，消除静态误差。

缺点：

需要经验来确定判断误差的大小，在什么时候使用积分分离比较合适，也就是误差多大的时候取消积分。

应用：
主要用于消除余差，该方法特别适用于生产设备启动阶段的控制。

C语言实现：只需要添加一句判断语句和对积分处理。

无积分分离式的PID：

sptr->Error_sum+=sptr->iError;//积分累加 iIncpid=sptr->Proportion * sptr->iError // P +sptr->Integral * sptr->Error_sum // I +sptr->Derivative * (sptr->iError-sptr->Error1); // D 

积分分离式PID：

 #include<math.h> int index=0;//积分分离标志 //积分分离处理 if(abs(sptr->iError)> 40) sptr->index=0; else { sptr->index=1; sptr->Error_sum+=sptr->iError;//积分累加 } iIncpid=sptr->Proportion * sptr->iError // P +sptr->Integral * （sptr->Error_sum * index） // I +sptr->Derivative * (sptr->iError-sptr->Error1); // D 

2、变速积分PID：

变积分PID可以看作是积分分离式PID的变体，积分分离式PID 积分的的权重是1或者0，而变积分PID积分的权重会动态变化。取决于偏差，偏差越大，积分越慢。

优缺点和积分分离式PID差不多，只不过，这个变速积分PID更加科学。

积分分离式PID：

#include<math.h> #define I_MAX 40 #define I_MIN 5 int index=0;//积分分离标志 //变积分处理 if(abs(sptr->iError)> I_MAX) index=0; else if(abs(sptr->iError)< I_MIN) index=1; else index=(I_MAX - abs(sptr->iError) / (I_MAX - I_MIN); if(index!=0) sptr->Error_sum+=sptr->iError;//积分累加 iIncpid=sptr->Proportion * sptr->iError // P +sptr->Integral * （sptr->Error_sum * index） // I +sptr->Derivative * (sptr->iError-sptr->Error1); // D //变速积分也可以这样处理:更加灵活 if(fabs(sptr->iError)> I_MAX) index=0; else if(fabs(sptr->iError)< I_MIN) index=1; else if(fabs(sptr->iError>10&&abs(sptr->iError)<20)) index=0.4; else if(fabs(sptr->iError>30&&abs(sptr->iError)<50)) index=0.8; else index=(I_MAX - abs(sptr->iError) / (I_MAX - I_MIN); 

五、两种针对微分的PID

不完全微分PID：

微分的PID控制算法，是减少微分作用的副作用的一些算法。我们知道，当系统引入微分作用得时候会，引进高频干扰。为了抑制这种干扰，便引入低通滤波器。

优点：
对周期性干扰具有良好的抑制作用
适用于波动频率较高的场合