大家好，欢迎来到IT知识分享网。
这里高斯滤波，也叫高斯模糊。
应用：高斯滤波是一种线性平滑滤波器，对于服从正态分布的噪声有很好的抑制作用。在实际场景中，我们通常会假定图像包含的噪声为高斯白噪声，所以在许多实际应用的预处理部分，都会采用高斯滤波抑制噪声，如车牌识别等。
opencv函数声明:
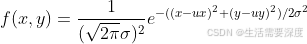
其中不必纠结于系数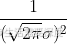
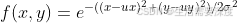
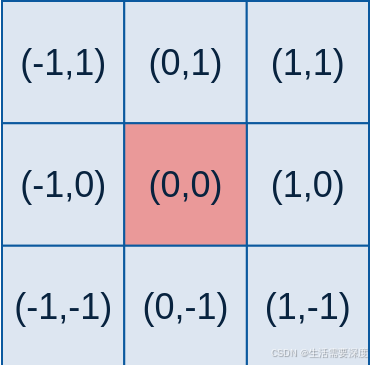
,因为它只是一个常数！并不会影响互相之间的比例关系，并且最终都要进行归一化，所以在实际计算时我们是忽略它而只计算后半部分:
其中(x,y)为掩膜内任一点的坐标，(ux,uy)为掩膜内中心点的坐标，在图像处理中可认为是整数；σ是标准差。
例如：要产生一个3×3的高斯滤波器模板，以模板的中心位置为坐标原点进行取样。模板在各个位置的坐标，如下所示（x轴水平向右，y轴竖直向下）
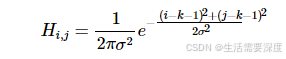
这样计算出来的模板有两种形式：小数和整数。
首先我们要确定我们生产掩模的尺寸wsize，然后设定高斯分布的标准差。生成的过程，我们首先根据模板的大小，找到模板的中心位置center。 然后就是遍历，根据高斯分布的函数，计算模板中每个系数的值。
最后模板的每个系数要除以所有系数的和。这样就得到了小数形式的模板。
3×3,σ=0.8的小数型模板：
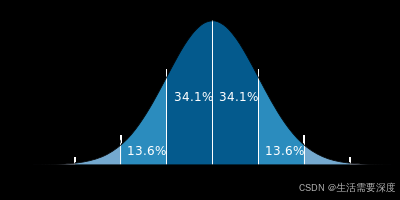
来看下一维高斯分布的概率分布密度图：
于是我们有如下结论：σ越小分布越瘦高，σ越大分布越矮胖。
只处理单通道或者三通道图像，模板生成后，其滤波（卷积过程）就比较简单了。不过，这样的高斯滤波过程，其循环运算次数为m×n×ksize×ksize，其中m，n为图像的尺寸；ksize为高斯滤波器的尺寸。这样其时间复杂度为O(ksize2)，随滤波器的模板的尺寸呈平方增长，当高斯滤波器的尺寸较大时，其运算效率是极低的。为了，提高滤波的运算速度，可以将二维的高斯滤波过程分解开来。
首先得到一维高斯函数的模板，在卷积（滤波）的过程中，保持行不变，列变化，在水平方向上做卷积运算；接着在上述得到的结果上，保持列不边，行变化，在竖直方向上做卷积运算。 这样分解开来，算法的时间复杂度为O(ksize)，运算量和滤波器的模板尺寸呈线性增长。
效果
免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/129988.html
