大家好,欢迎来到IT知识分享网。
1. 正交矩阵
标准正交向量组:
向量组 q 1 q 2 q 3 . . . q n q_1\ q_2\ q_3…\ q_n q1 q2 q3… qn满足
q i ⊤ q j = { 0 , i ≠ j 1 , i = j q_i^{\top}q_j= \begin{cases} 0,\quad i \ne j\\1,\quad i = j \end{cases} qi⊤qj={
0,i=j1,i=j
Q = [ q 1 q 2 q 3 . . . q n ] Q ⊤ = [ q 1 ⊤ q 2 ⊤ q 3 ⊤ . . . q n ⊤ ] Q ⊤ Q = I Q=[q_1\ q_2\ q_3…\ q_n]\\ Q^{\top}= \begin{bmatrix} q_1^{\top}\\q_2^{\top}\\q_3^{\top}\\…\\q_n^{\top} \end{bmatrix}\\ Q^{\top}Q=I Q=[q1 q2 q3… qn]Q⊤=
q1⊤q2⊤q3⊤…qn⊤
Q⊤Q=I
如果 Q Q Q是方阵
Q ⊤ = Q − 1 Q^{\top}=Q^{-1} Q⊤=Q−1
置换矩阵是标准正交矩阵
p e r m Q = [ 0 0 1 1 0 0 0 1 0 ] p e r m Q ⊤ = [ 0 1 0 0 0 1 1 0 0 ] permQ= \begin{bmatrix} 0 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0\\ \end{bmatrix}\\ permQ^{\top}= \begin{bmatrix} 0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0\\ \end{bmatrix} permQ=
010001100
permQ⊤=
001100010
Q Q Q是标准正交矩阵有什么好处呢?
( Q Q ⊤ ) ( Q Q ⊤ ) = Q ( Q ⊤ Q ) Q ⊤ = Q Q ⊤ (^{\top})(^{\top}) = Q(Q^{\top}Q)Q^{\top} = ^{\top} (QQ⊤)(QQ⊤)=Q(Q⊤Q)Q⊤=QQ⊤
2. 正交化法
G r a h a m − S c h m i d t Graham-Schmidt Graham−Schmidt方法
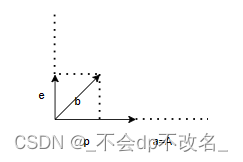
考虑二维的情况
e = B = b − p e ⊥ A p = A X ^ = A A ⊤ b A ⊤ A = A ⊤ b A ⊤ A A A ⊤ B = A ⊤ ( b − A ⊤ b A ⊤ A A ) = 0 e =B=b-p\\e \perp A\\ p=A\hat{X}=A \frac{A^{\top}b}{A^{\top}A}= \frac{A^{\top}b}{A^{\top}A} A\\ A^{\top}B=A^{\top}(b- \frac{A^{\top}b}{A^{\top}A} A)=0 e=B=b−pe⊥Ap=AX^=AA⊤AA⊤b=A⊤AA⊤bAA⊤B=A⊤(b−A⊤AA⊤bA)=0
得到正交向量后再将其标准化
q 1 = A ∣ A ∣ , q 2 = B ∣ B ∣ q_1=\frac{A}{|A|},q_2=\frac{B}{|B|} q1=∣A∣A,q2=∣B∣B
举个例子
a = [ 1 1 1 ] b = [ 1 0 2 ] a= \begin{bmatrix} 1\\1\\1 \end{bmatrix}\\ b= \begin{bmatrix} 1\\0\\2 \end{bmatrix}\\ a=
111
b=
102
C ( A , B ) = C ( Q ) C(A,B)=C(Q) C(A,B)=C(Q)
最终化简一定是
Q = A R Q=AR Q=AR
R R R是上三角矩阵,进行列表换得到标准正交矩阵。
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/131172.html