IIR数字滤波器原理，设计方法及嵌入式应用

大家好，欢迎来到IT知识分享网。

目录

一、IIR数字滤波器原理

二、MATLAB/simulink设计方法及示例代码

三、基于stm32的嵌入式应用及代码

一、IIR数字滤波器原理

IIR(Infinite-duration Impulse Responses) 即无限长脉冲响应滤波器。

以设计IIR巴特沃斯低通滤波器为例，其离散形式为

其直接II型结构为：

二、MATLAB/simulink设计方法及示例代码

设计步骤：

Step1：对原时域信号进行傅里叶变换，得到原信号的频谱图；

举例：原信号是基波频率为10Hz、干扰信号为100Hz、300Hz的混合信号

clear all; close all; fs = 1000; %采样频率 1KHz T = 1;%时间宽度，可以理解为采样时间长度 ts = 1/fs;%数据之间采样间隔 N = T*fs;%采样点数T/ts t = (0:N-1)*ts; %基波：幅值为3的1Hz正弦波 Signal_Original_1 = 3*sin(20*pi*t); %噪声函数 赋值为基波的1/3 100hz 300hz 正弦波 Noise_White_1 = sin(2*pi*100*t)+sin(2*pi*300*t); %构造的混合信号 Mix_Signal = Signal_Original_1 + Noise_White_1; figure(1); subplot(211); plot(t,Mix_Signal); xlabel('时间t(s)'); title('带噪声信号'); %快速傅里叶变换 Y = fft(Mix_Signal); P2 = abs(Y/N); % 计算双侧频谱 P2 P1 = P2(1:N/2+1); % 将P2的前半段信号赋给P1，P1即是我们关心的部分 P1(2:end-1) = 2*P1(2:end-1); %计算每个信号的双侧频谱和单侧频谱。 f = fs*(0:(N/2))/N;%采样频率fs,因此只看fs/2内的信号 subplot(212); plot(f,P1,'r'); title('带噪声信号'); xlabel('频率f(Hz)'); ylabel('|P1(f)|'); 

Step2：选择需要保留的频率，设计满足需求的滤波器；

根据上述示例，需要保存的频率为10Hz，选用低通滤波器，以IIR巴特沃斯低通滤波器为例,可选取截止频率为30Hz。通过代码确认满足需求的滤波器阶次。

其中，通带波纹：是指在滤波器的频响中通带的最大幅值和最小幅值的差，正常的滤波器一般通带纹波小于1db，不过也视情况而定，通带纹波会导致通带内的信号幅值大小有变化，对一些要求高的系统，纹波越小越好。通带纹波和滤波器的阶数有关系，阶数越大纹波越小。

阻带衰减：滤波器有部分频率是通，部分是阻。但是阻的部分，未必能够全部阻隔，而只有部分衰减，部分留下来，因此最小衰减就可以描述它阻碍该阻碍的波段的能力的高低（理想状态是100%衰减），最小衰减越大，则能力越好。

%IIR滤波器设计 NN=0; % 阶数 Fp=5; % 通带截止频率5Hz Fc=40; % 阻带截止频率30Hz Rp=1; % 通带波纹最大衰减为1dB，最好情况为1dB Rs=30; % 阻带衰减为30dB,截止频率的10倍频程时，衰减30dB,数值越大阻止能力越强。 %计算最小滤波器阶数 na=sqrt(10^(0.1*Rp)-1); ea=sqrt(10^(0.1*Rs)-1); NN=ceil(log10(ea/na)/log10(Fc/Fp)); 

Step3：使用fdatool(filterDesigner)工具箱，按照需求进行选择；

—>在MATLAB命令窗口输入 fdatool(或filterDesigner)；

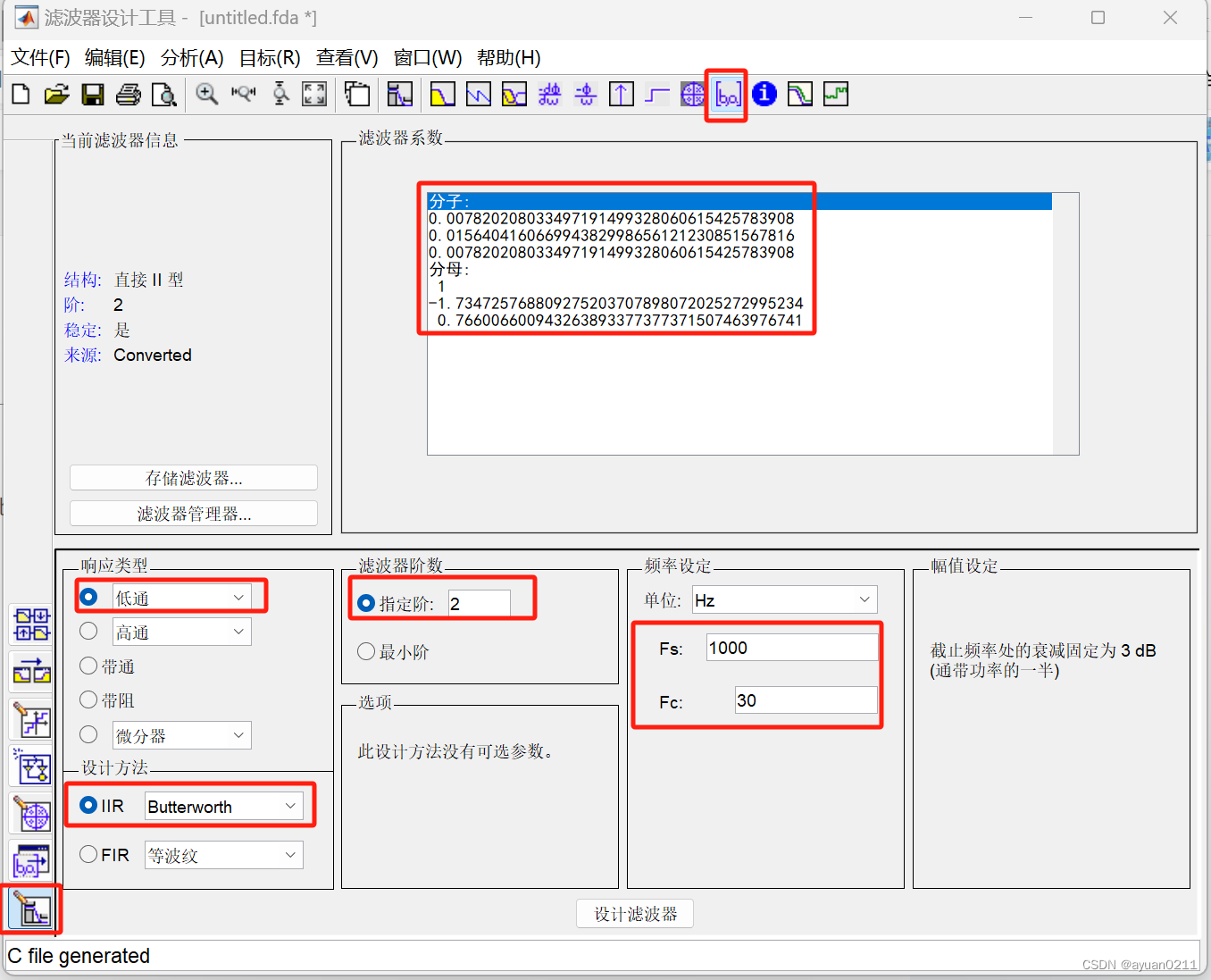
—>打开滤波器设计工具箱,设计选择低通，巴特沃斯 2阶 采样频率fs=1000,截止频率fc=50后，点击设计滤波器，选择[b,a]图标即可查看参数，但需要通过“编辑”选项，选择“转换为单节”，才能得到普遍意义上的滤波器系数，如图所示。

Step4：验证数字滤波器性能；

为验证滤波器设计是否达到效果，需要进行滤波验证。

首先，生成simulink单元模型—>选择，选择使用基本元素构建模型，点击实现模型。

以此得到滤波器系数b,a，在MATLAB中形成代码如下：

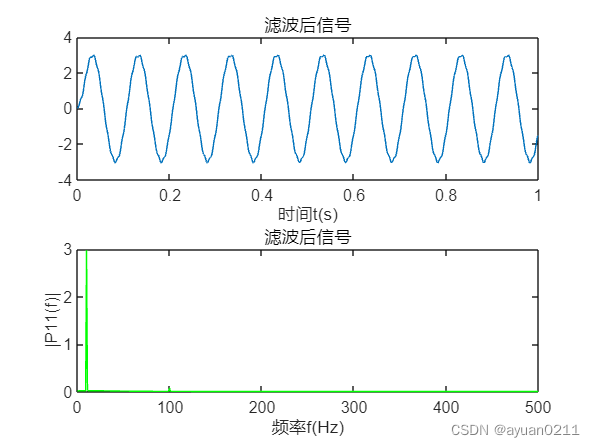
a2=-1.; a3=0.; b1=0.00; b2=0.0; b3=0.00; delay0=0; delay1=0; delay2=0; for i = 1:N delay0 = Mix_Signal(i)-a2*delay1-a3*delay2; output(i) = b1*delay0+b2*delay1+b3*delay2; delay2=delay1; delay1=delay0; end hold on; figure(2); subplot(211); plot(t,output); xlabel('时间t(s)'); title('滤波后信号'); %快速傅里叶变换 OY = fft(output); P21 = abs(OY/N); % 计算双侧频谱 P2 P11 = P21(1:N/2+1); % 将P2的前半段信号赋给P1，P1即是我们关心的部分 P11(2:end-1) = 2*P11(2:end-1); %计算每个信号的双侧频谱和单侧频谱。 f = fs*(0:(N/2))/N;%采样频率fs,因此只看fs/2内的信号 subplot(212); plot(f,P11,''); title('滤波后信号'); xlabel('频率f(Hz)'); ylabel('|P11(f)|');

对比原信号和滤波后信号：

figure(3); plot(t,[s0;output]); legend('原信号','IIR滤波后信号'); xlabel('时间t(s)'); title('信号');

结果分析：截止频率选择30Hz时，幅值上没有衰减，相位上存在一定滞后。也说明数字滤波器在采样后与模拟滤波器存在一定差异。

三、基于stm32的嵌入式应用及代码

为了应用于stm32,需要重复目录二。

import通过jscope或采集系统得到的时域数据，设置采样频率与上述设备一致，设置一周期以上时宽后，进行傅里叶变换（fft）,确定截止频率fc，从而设计滤波器，通过滤波器工具箱得到滤波系数。

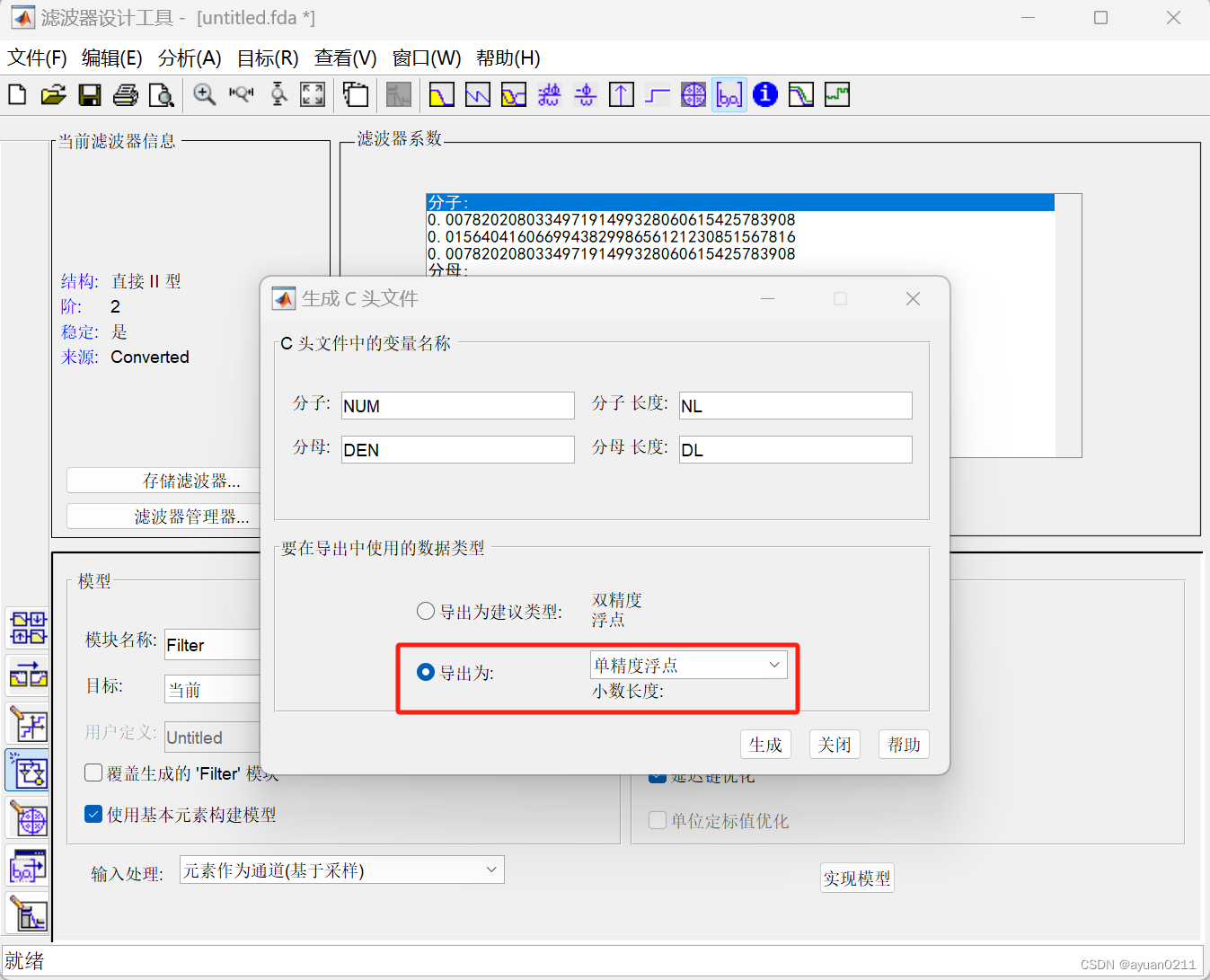
点击目标，生成C头文件，选择导出类型为单精度即可满足stm32需求。

生成C头文件后，用VSCode打开，得到滤波器系数如下：

const int NL = 3; const real32_T NUM[3] = { 0.00, 0.0, 0.00 }; const int DL = 3; const real32_T DEN[3] = { 1, -1., 0. };

在stm32中实现对应程序如下：

static float NUM[3]={0.00, 0.0, 0.00}; static float DEN[3]={1,-1.,0.}; //子函数 float IIR_LPF_FILTER(float input,float* NUM,float* DEN) { float output; static float delay[3]={0}; delay[0] = input - DEN[1]*delay[1]-DEN[2]*delay[2]; output = NUM[0]*delay[0]+NUM[1]*delay[1]+NUM[2]*delay[2]; delay[2]=delay[1]; delay[1]=delay[0]; return output; } //主函数调用 void main() { float input; input = sdp(); IIR_LPF_FILTER(input,NUM,DEN); } 

至此，即完成了基于STM32的二阶直接II型巴特沃斯低通滤波器。

参考：

https://zhuanlan.zhihu.com/p/

一文看懂MATLAB 滤波器设计（IIR滤波器、FIR滤波器）及单片机实现 – 知乎 (zhihu.com)

MATLAB中FFT的用法 – 知乎 (zhihu.com)

通带纹波、阻带纹波、通带最大波纹和阻带最小衰减-CSDN博客