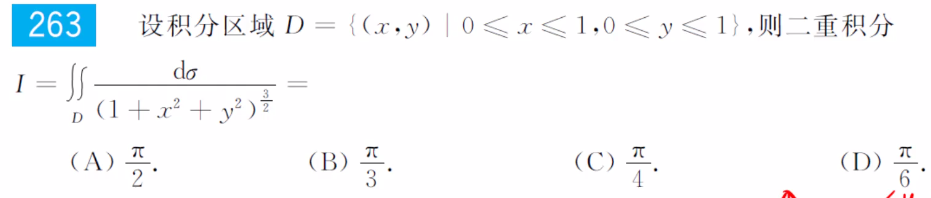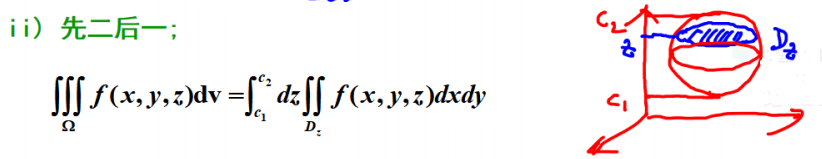大家好,欢迎来到IT知识分享网。
Ch10. 重积分
(一) 二重积分
1.二重积分的概念
(1)二重积分的定义
∬ D f ( x , y ) d σ = lim λ → 0 ∑ i = 1 n f ( x i , y i ) Δ σ i \iint\limits_Df(x,y)dσ=\lim\limits_{λ→0}\sum\limits_{i=1}^nf(x_i,y_i)Δσ_i D∬f(x,y)dσ=λ→0limi=1∑nf(xi,yi)Δσi
当 f ( x , y ) ≡ 1 , ∬ D 1 d σ = S f(x,y)≡1,\iint\limits_D1dσ=S f(x,y)≡1,D∬1dσ=S
例题1:10年4. 利用二重积分的定义求极限
答案:D
(2)二重积分的几何意义
曲顶柱体的体积
2.二重积分的性质
(1)不等式性质
①保号性:若 f ( x , y ) ≤ g ( x , y ) f(x,y)≤g(x,y) f(x,y)≤g(x,y),则 ∬ D f ( x , y ) d x d y ≤ ∬ D g ( x , y ) d x d y \iint\limits_D f(x,y)dxdy≤\iint\limits_D g(x,y)dxdy D∬f(x,y)dxdy≤D∬g(x,y)dxdy
②保号性推论: ∣ ∬ D f ( x , y ) d x d y ∣ ≤ ∬ D ∣ f ( x , y ) ∣ d x d y |\iint\limits_D f(x,y)dxdy|≤\iint\limits_D |f(x,y)|dxdy ∣D∬f(x,y)dxdy∣≤D∬∣f(x,y)∣dxdy 【积分的绝对值≤绝对值的积分】
③估值定理: m σ ≤ ∬ D f ( x , y ) d x d y ≤ M σ mσ≤\iint\limits_D f(x,y)dxdy≤Mσ mσ≤D∬f(x,y)dxdy≤Mσ
(2)二重积分的积分中值定理
∬ D f ( x , y ) d σ = f ( ξ , n ) ⋅ S \iint\limits_Df(x,y)dσ=f(ξ,n)·S D∬f(x,y)dσ=f(ξ,n)⋅S
例题1: 保号性
例题2: 保号性
分析:
答案:A
例题3:09年2. 二重积分的奇偶对称性、保号性
答案:A
3.二重积分的计算
重积分化为累次积分:二重积分化为两次定积分
(1)直角坐标
(1)X型区域:先y后x
∬ D f ( x , y ) d σ = ∫ a b d x ∫ y 1 ( x ) y 2 ( x ) f ( x , y ) d y \iint\limits_Df(x,y)dσ=\int_a^bdx\int_{y_1(x)}^{y_2(x)}f(x,y)dy D∬f(x,y)dσ=∫abdx∫y1(x)y2(x)f(x,y)dy
(2)Y型区域:先x后y
∬ D f ( x , y ) d σ = ∫ c d d y ∫ x 1 ( y ) x 2 ( y ) f ( x , y ) d x \iint\limits_Df(x,y)dσ=\int_c^ddy\int_{x_1(y)}^{x_2(y)}f(x,y)dx D∬f(x,y)dσ=∫cddy∫x1(y)x2(y)f(x,y)dx
(2)极坐标

4.圆心既不在原点,也不在坐标轴上时:平移 + 极坐标
{ x − x 0 = ρ cos θ y − y 0 = ρ sin θ \left\{\begin{aligned} x-x_0 & = ρ\cosθ\\ y-y_0 & = ρ\sinθ \end{aligned}\right. {
x−x0y−y0=ρcosθ=ρsinθ
5.广义极坐标 (D为椭圆域)
x 2 a 2 + y 2 b 2 = 1 \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 a2x2+b2y2=1:
令 u = x a , v = y b u=\dfrac{x}{a},v=\dfrac{y}{b} u=ax,v=by,则上述椭圆域可化为 圆域: u 2 + v 2 = 1 u^2+v^2=1 u2+v2=1
例题1:880 P35 二T7 椭圆域
(3)对称性
①奇偶对称性:关于坐标轴对称
②轮换对称性:关于 y = x y=x y=x 对称
例题4:660 T263 轮换对称性的推广
分析:
答案:D
(4)交接积分次序:画域、重新定限(二重积分化二次积分)
①直角坐标 交换积分次序
①画域:画出二重积分区域D
②重新定限:将X型区域变成Y型,或将Y型区域变为X型。
分析: − ∫ − 1 0 d y ∫ 2 1 − y f ( x , y ) d x -\int_{-1}^0dy\int_2^{1-y}f(x,y)dx −∫−10dy∫21−yf(x,y)dx,注意dx的积分限故意写反了!要先提个负号出来!

答案: − ∫ 1 2 d x ∫ 1 − x 0 f ( x , y ) d y -\int_1^2dx\int_{1-x}^0f(x,y)dy −∫12dx∫1−x0f(x,y)dy
例题2: 极坐标化直角坐标
分析:ρ=cosθ,则ρ²=ρcosθ,即x²+y²=x,偏心圆
答案:D
例3: 直角坐标化极坐标
例题4:06年8. 二重积分:极坐标与直角坐标的转换
分析:①画域 ②重新定限
答案:C
②极坐标 交换积分次序
法一:先θ后r:r=c,是绕坐标原点的一组圆弧。
法二:把ρ,θ当作y,x,重新画直角坐标下的曲线。
例题1:660 T109
例题2:880 P35 二、T6
(二) 三重积分
1.三重积分的概念
2.三重积分的性质
3.三重积分的计算
(1)直角坐标
①先一后二(先单后重) / 投影法
∭ Ω f ( x , y , z ) d v = ∬ D x y d x d y ∫ z 1 ( x , y ) z 2 ( x , y ) f ( x , y , z ) d z \iiint\limits_Ωf(x,y,z){\rm d}v=\iint\limits_{D_{xy}}{\rm d}x{\rm d}y\int_{z_1(x,y)}^{z_2(x,y)}f(x,y,z){\rm d}z Ω∭f(x,y,z)dv=Dxy∬dxdy∫z1(x,y)z2(x,y)f(x,y,z)dz
例题1:23年19. 三重积分的计算:投影法
答案: ( 2 − 2 ) π R 3 (2-\sqrt{2})πR³ (2−2)πR3
②先二后一 / 截面法
∭ Ω f ( x , y , z ) d v = ∫ z 1 z 2 d z ∬ D z f ( x , y , z ) d x d y \iiint\limits_Ωf(x,y,z){\rm d}v=\int_{z_1}^{z_2}dz\iint\limits_{D_z}f(x,y,z){\rm d}x{\rm d}y Ω∭f(x,y,z)dv=∫z1z2dzDz∬f(x,y,z)dxdy
对于f里只含z的三重积分,建议使用截面法: ∭ Ω f ( z ) d v = ∫ z 1 z 2 f ( z ) d z ∬ D z d x d y = ∫ z 1 z 2 f ( z ) ⋅ D z d z \iiint\limits_Ωf(z){\rm d}v=\int_{z_1}^{z_2}f(z)dz\iint\limits_{D_z}{\rm d}x{\rm d}y=\int_{z_1}^{z_2}f(z)·D_zdz Ω∭f(z)dv=∫z1z2f(z)dzDz∬dxdy=∫z1z2f(z)⋅Dzdz
例题2:18年17. 第二类曲面积分 → 高斯公式 三重积分 → 截面法 二重积分 → 极坐标 定积分 第二类曲面积分\xrightarrow{高斯公式} 三重积分\xrightarrow[]{截面法}二重积分\xrightarrow[]{极坐标}定积分 第二类曲面积分高斯公式三重积分截面法二重积分极坐标定积分
(2)柱坐标 (类似二重的极坐标)
2.柱坐标本质:先直角坐标,再极坐标
3. d v = ρ d ρ d θ d z dv=ρdρdθdz dv=ρdρdθdz
例题1:10年12题的中间步骤
(3)球面坐标
d v = d x d y d z = r 2 sin φ d r d φ d θ ∭ Ω f ( x , y , z ) = ∭ Ω F ( r , φ , θ ) r 2 sin φ d r d φ d θ = ∫ α β d θ ∫ α ′ β ‘ sin φ d φ ∫ r 1 r 2 F ( r , φ , θ ) r 2 d r {\rm d}v={\rm d}x{\rm d}y{\rm d}z=r²\sinφ{\rm d}r{\rm d}φ{\rm d}θ\\[3mm] \iiint\limits_Ωf(x,y,z)=\iiint\limits_ΩF(r,φ,θ)r²\sinφ{\rm d}r{\rm d}φ{\rm d}θ=\int_α^β{\rm d}θ\int_{α’}^{β‘}\sinφ{\rm d}φ\int_{r_1}^{r_2}F(r,φ,θ)r²{\rm d}r dv=dxdydz=r2sinφdrdφdθΩ∭f(x,y,z)=Ω∭F(r,φ,θ)r2sinφdrdφdθ=∫αβdθ∫α′β‘sinφdφ∫r1r2F(r,φ,θ)r2dr
解2: ∭ f ( z ) d v \iiint f(z)dv ∭f(z)dv,用截面法:根据勾股定理, r 2 = R 2 − z 2 = 1 − z 2 ∴ D z = π r 2 = π ( 1 − z 2 ) r^2=R^2-z^2=1-z^2 ∴D_z=πr^2=π(1-z^2) r2=R2−z2=1−z2∴Dz=πr2=π(1−z2)
答案: 4 15 π \dfrac{4}{15}π 154π
答案: ( 2 − 2 ) π R 3 (2-\sqrt{2})πR³ (2−2)πR3
例题3:24李林四(一)17. 球面坐标
(4)对称性
①关于坐标面的对称性(偶倍奇零)
关于某坐标轴对称,或关于某坐标平面对称,奇函数积分为0.
例题1:07年18. 椭圆域:也可以偶倍奇零。看到奇函数就要考虑是否有对称性可以直接得0
答案: π − 0 = π π-0=π π−0=π
②轮换对称性
轮换对称性:若积分区域Ω 轮换x、y、z(使y代替x,z代替y,x代替z),函数不变,则三者地位相等,可以互相代替
例题1:15年12. 求三重积分:轮换对称性 + 截面法
分析:
答案: 1 4 \dfrac{1}{4} 41
例题2:18年12. 轮换对称性
答案: − π 3 -\dfrac{π}{3} −3π
本题在2018年时的难度系数为0.026,低的惊人,只有2.6%的人做对了。可见轮换对称性的杀伤力。
例题3:07年14. 关于坐标面的对称性、轮换对称性
分析: ∣ x ∣ + ∣ y ∣ + ∣ z ∣ = 1 |x|+|y|+|z|=1 ∣x∣+∣y∣+∣z∣=1 是正八面体 
考虑曲面Σ关于yOz平面对称,则关于x的奇函数的曲面积分为0,即 ∯ Σ x d S = 0 \oiint\limits_Σx\ {\rm d}S=0 Σ∬x dS=0
∴ ∯ Σ ( x + ∣ y ∣ ) d S = ∯ Σ ∣ y ∣ d S = 轮换对称性 1 3 ∯ Σ ( ∣ x ∣ + ∣ y ∣ + ∣ z ∣ ) d S = 1 3 ∯ Σ d S \oiint\limits_Σ(x+|y|)\ {\rm d}S=\oiint\limits_Σ|y|\ {\rm d}S\xlongequal{轮换对称性}\dfrac{1}{3}\oiint\limits_Σ(|x|+|y|+|z|)\ {\rm d}S=\dfrac{1}{3}\oiint\limits_Σ{\rm d}S Σ∬(x+∣y∣) dS=Σ∬∣y∣ dS轮换对称性31Σ∬(∣x∣+∣y∣+∣z∣) dS=31Σ∬dS
观察该正八面体 ∣ x ∣ + ∣ y ∣ + ∣ z ∣ = 1 |x|+|y|+|z|=1 ∣x∣+∣y∣+∣z∣=1,其在第一卦限上的表面积为一个正三角形,边长为 2 \sqrt{2} 2,则正三角形的面积为 3 4 a 2 = 3 4 × 2 = 3 2 \dfrac{\sqrt{3}}{4}a²=\dfrac{\sqrt{3}}{4}×2=\dfrac{\sqrt{3}}{2} 43a2=43×2=23
则 1 3 ∯ Σ d S = 1 3 × 8 × 3 2 = 4 3 3 \dfrac{1}{3}\oiint\limits_Σ{\rm d}S=\dfrac{1}{3}×8×\dfrac{\sqrt{3}}{2}=\dfrac{4\sqrt{3}}{3} 31Σ∬dS=31×8×23=343

答案: 4 3 3 \dfrac{4\sqrt{3}}{3} 343
(5)当 f(x,y,z)=1时, ∭ Ω d v = V \iiint\limits_Ω{\rm d}v=V Ω∭dv=V
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/131545.html