力矩的大小、方向及相关说明

大家好，欢迎来到IT知识分享网。

力矩是影响物体转动的物理量，力矩计算分两种：

力对固定点的力矩

• 力矩的定义

  力对点的力矩定义为在参考坐标系中力的作用点的位置矢量 叉乘 力矢量，用数学公式表示，即：

  $$\vec{M}=\vec{r}\times \vec{F}$$

  下图形象展示：

  

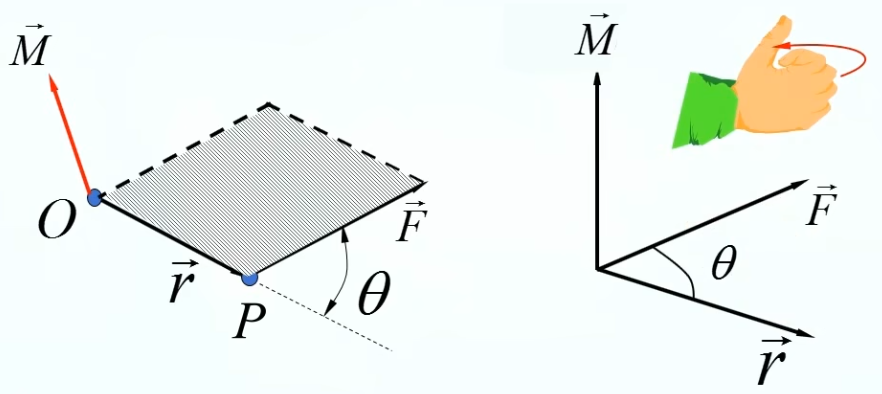
  • 力矩的方向

    即叉乘的方向，可以用右手定则确定，即：大拇指垂直于四指，四指首先指向位置向量的方向 $\vec{r}$ 的方向，然后以小于$\pi$ 的角度转向力矢量$\vec{F}$，大拇指的指向即力矩的方向

    

    众所周知，叉乘的两个向量之间位置不能随便变换

    力矩的方向垂直于$\vec{r}$ 和 $\vec{F}$ 所组成的平面

  • 力矩的大小
    • 计算方法一

      既然力矩的计算公式是一个叉乘，那么其大小即$\vec{M}$的模，即有：

      

    • 计算方法二

      由力矩的定义：力矩的大小等于力和力臂的乘积，力臂即力的作用线到作用点的距离，如下图所示的$d$：

      $$ d=r \cdot sin\theta $$ 所以力矩的大小为 $$ M=F \cdot d=F \cdot r \cdot sin\theta $$

      其实$\vec{M}$ 的模也可以这样计算

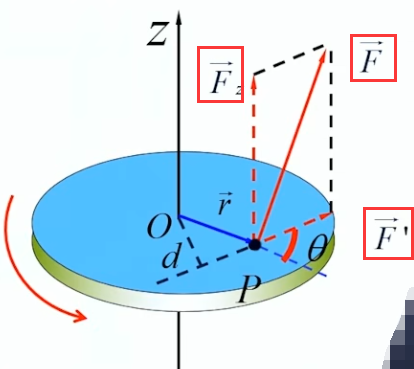
力对固定轴的力矩

力对某轴的力矩是度量力对该轴转动的效应的物理量，也就是说，力矩的方向会沿着转动轴的方向，所以这里的方向和大小的计算和上面略有不同。

• 力矩的方向和大小说明

  力有一个作用点，该作用点对于转动轴会对应一个平面，转动轴是这个平面的法线。

  因此，我们可以将力分解到两个方向，如下图所示：

  

  分解矢量1 ${\vec{F}}_z$ 是沿着轴的方向的，它不会产生力矩

  分解矢量2 ${\vec{F}}^{\prime }$ 在转动平面内，它产生力矩，并可以由上述右手定则验证其方向也是沿着转动轴的方向的

  对于分解矢量2 ${\vec{F}}^{\prime }$，就和上面力对点的力矩计算方法一样了，其中点即转动轴和平面的交点$O$

  • 力矩大小
    $$M=F^{\prime }\cdot r\cdot sin\theta$$
    
  • 力矩方向

    $\vec{M}=\vec{r}\times {\vec{F}}^{\prime }$ 的方向

  • 补充说明

    对于三维空间中的转动，可能不只有单独的固定轴，如可能有X-Y-Z三条轴，力对这三条轴的力矩的计算方式和上面所述一样

    此外，力的分解方式也不只有上述的形式，可以根据具体需求进行分析

    总之，本文描述了最本质的方法。

本文主要参考：3.2 力矩 哔哩哔哩 bilibili