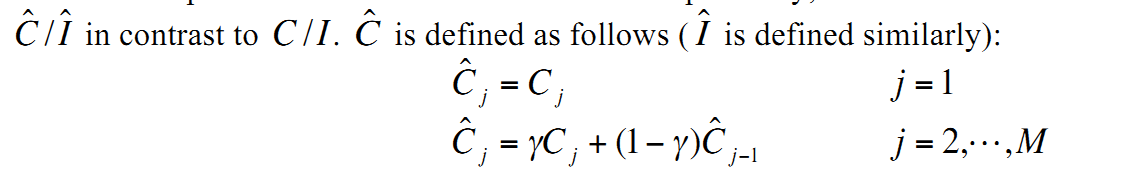点击率预估方法总结

大家好，欢迎来到IT知识分享网。

                                        点击率预估方法总结

点击率预估方法总结

1. 普通方法

p = C / I

1. 可能有的帖子曝光数很少，甚至为 0，以至于得不到准确的 CTR。至于为什么会有0，这和日志统计有关系，因为曝光和点击日志是分开记录的，而日志ETL又是以自然单位时间来进行的，所以对于某个自然时间窗口，帖子的点击事件捕获到了，但是它的曝光事件出现在前面的时间窗口。

至于为什么会很少，那是因为在自然竞争下，帖子的曝光分布绝大多数不是平均的，甚至也不是正态分布的，而是头部很高、尾巴很长的长尾分布。

2. 直接使用帖子的点击数和曝光数，没有考虑曝光事件和点击事件里面的噪音，或者说系统误差，甚至是作弊行为。

2. 贝叶斯平滑

p = C + α / (I + α + β )

贝叶斯平滑，实际上是给了每个帖子一个先验的 点击率， 这个先验的点击率就是 α / ( α + β )，意思就是在正式做实验之前，我们认为已经做了 α + β 次试验，成功的次数为 α 。

至于先验概率参数怎么获取，雅虎的专家们曾经发表过一篇论文[1]提供了一些思路。

因为二项分布的先验分布是Beta分布, 这里可以看成是根据若干个Beta分布的样本估计Beta分布的参数。

参数估计代码：

 # click_count, show_count # this method takes time def do_smooth(data_list): a, b, i = 1.0, 1.0, 0 da, db = a, b while i < 2000 and (da > 1.0E-10 or db > 1.0E-10): x1, y1, x2 = 0.0, 0.0, 0.0 for lineList in data_list: # lineList[0] is click_times, lineList[1] is show_times x1 += sp.digamma((lineList[0]) + a) - sp.digamma(a) y1 += sp.digamma((lineList[1]) + a + b) - sp.digamma(a + b) x2 += sp.digamma((lineList[1]) - (lineList[0]) + b) - sp.digamma(b) na, nb = a, b a *= (x1 / y1) b *= (x2 / y1) da, db = abs(a - na), abs(b - nb) i += 1 print i, a, b return a, b

3. 时间衰减

感谢雅虎专家们，同样是上面那篇论文中提到的时间平滑（我叫它时间衰减）。意思其实是随着时间推移，发生在过去的点击事件要做衰减，原文的说法是加权平均，过去的点击权重小。我实现的时候还考虑了时间范围。注意衰减我只对点击进行衰减。

 / * 在一定范围内衰减 * * @param diffdays * @return */ private def getTimeDecay(diffdays: Double): Double = { if (diffdays > DAYS_LIMIT) { MConstant.GAMA * Math.pow(1 - MConstant.GAMA, diffdays) } else { 1.0 } } 

4. 位置纠偏

位置纠偏或者叫位置衰减，其与时间衰减的原理类似，即发生在不同时间、空间上的点击事件对我们要预测的用户行为影响程度是不同的，这一点和subsampling有很大关系。北冥乘海生@刘鹏老师在《计算广告》课程中有讲到，使用归一化点击率来预测广告的点击率能够消除展示位置带来的影响。是的，这里的归一化就是要让帖子的每一次点击事件的影响转化为帖子这次点击事件相对同样位置点击事件的相对影响，朴素一点讲，你牛不牛逼要和你同一起跑线的人比，你做的事情牛不牛逼要和相同环境条件下的事情比。

 val part_decay = part_filter.map(p => { val infoid = p(0).toLong val diffdays = p(1) val pos = p(2) val shows = p(3) val clicks = p(4) val time_decay = 1 val max_pos = pos_ctr_arr.length assert(max_pos > 0) val b = if (pos >= max_pos) pos_ctr_arr(max_pos - 1) else pos_ctr_arr(pos.toInt - 1) assert(b > 0) val pos_decay = 1 / b val decay_clicks = clicks * time_decay * pos_decay val clicks_with_bayes = decay_clicks val shows_with_bayes = shows (infoid, (clicks_with_bayes, shows_with_bayes)) }).cache()

5. UCB方法

ucb方法，ctr=普通ctr加1.96*普通CTR标准差，标准差的计算可以探讨，暂考虑使用这一种；

主要原理是根据实时反馈预估帖子的曝光收益，假设我们还可以用点击率来描述的话。那么实时点击率计算公式如上，实质上是均值加上标准差，类似于 2δ 置信区间()，只不过这里取得是置信区间上界。为什么这样可以？或者说最优？为什么是2倍不是3倍？我暂时也不清楚。

 # the UCB algorithm using # (1 - 1/t) confidence interval using Chernoff-Hoeffding bound) # for details of this particular confidence bound, see the UCB1-TUNED section, slide 18, of: # http://lane.compbio.cmu.edu/courses/slides_ucb.pdf def UCB(estimated_beta_params): t = float(estimated_beta_params.sum()) # total number of rounds so far totals = estimated_beta_params.sum(1) successes = estimated_beta_params[:, 0] estimated_means = successes / totals # sample mean estimated_variances = estimated_means - estimated_means 2 # np.minimum 取两个数组相同位置最小的值构成一个新的数组 bound = np.sqrt(np.minimum(estimated_variances + np.sqrt(2 * np.log(t) / totals), 0.25) * np.log(t) / totals) UCB = estimated_means + bound return np.argmax(UCB) # the UCB algorithm - using fixed 95% confidence intervals # see slide 8 for details: # http://dept.stat.lsa.umich.edu/~kshedden/Courses/Stat485/Notes/binomial_confidence_intervals.pdf # UCB_bernolli 就是用均值+方差，即用上界来排序 # 当一个帖子的点击率稳定后，会依次选下一个均值+方差第二大、第三大的帖子，直到他们的点击率稳定 def UCB_bernoulli(estimated_beta_params): totals = estimated_beta_params.sum(1) # totals successes = estimated_beta_params[:, 0] # successes estimated_means = successes / totals # sample mean # ??? 平方的期望减去期望的平方才对呀？--二项分布方差公式p(1-p) estimated_variances = estimated_means - estimated_means 2 UCB = estimated_means + 1.96 * np.sqrt(estimated_variances / totals) return np.argmax(UCB)

6. Tompson采样

1. ctr=pymc.rbeta(1 + a, 1 + b)；

2. 帖子的点击事件服从伯努利分布，点击率先验服从Beta分布

3. 加1是防止a或者b为 0 ， 好像为 0 会出问题 

 贝叶斯平滑是把所有帖子放一起估计一个先验分布，Tompson采样是根据观测到的点击次数 a，未点击次数 b 来生成一个服从Beta( a, b ) 的 r 。

这样操作为什么可以？是不是最优？

 # 原理就是根据已有成功和失败次数建立点击率的Beta分布 # 使用时从beta分布中取一个随机数 # 根据随机数的大小排序 def Tompson_Sampling(estimated_beta_params): totals = estimated_beta_params.sum(1) # totals successes = estimated_beta_params[:, 0] # successes # return random beta value's index return np.argmax(pymc.rbeta(1 + successes, 1 + totals - successes))

7. 数据清洗

总结：

1. 在算法实践中发现，可比性 是一个贯穿始终的重要概念，不可比的东西无法形式化地放在同一空间进行计算。

2. 从过滤策略中发现，能够显著减小整体不确定性的东西比较重要，

参考：

1. Click-Through Rate Estimation for Rare Events in Online Advertising.Xuerui Wang, Wei Li, Ying Cui, Ruofei (Bruce) Zhang, Jianchang Mao Yahoo! Labs, Silicon Valley United States

2. Mcmahan H B, Holt G, Sculley D, et al. Ad click prediction: a view from the trenches[C]// ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2013:1222-1230.

3.刘鹏, 王超. 计算广告 : Computational advertising : 互联网商业变现的市场与技术[M]. 人民邮电出版社, 2015.