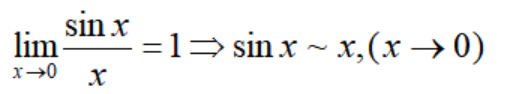无穷小量与无穷大量的阶

1.无穷量可分为高阶无穷，同阶无穷和等价无穷

2.等价无穷小是同阶无穷小的特殊情况,等价无穷大是同阶无穷大的特殊情况

3.任何x阶数都是一个无穷小量的高阶无穷小，则这个无穷小记为o(1)

4.两个高阶无穷小量相加或相减后依然为高阶无穷小

5.在含有多个高阶无穷的式子中，其极限由最高阶无穷大量或最低阶无穷小量决定

我们提到过以0为极限的变量称为无穷小量，这个变量可以是数列也可以是函数。但需要注意两种表达：

1

• 例1

• 例2

对于第二种情况，表明u和v趋近于0的速度在一个量级上，趋向的速度差不多。举个例子：

• 例3

注意，这里的u和v不一定是同阶无穷小，因为也有可能u是v的高阶无穷小。

• 例4

对于第三种情况，等价无穷小其实相当于同阶无穷小的一种特殊情况，是最重要的一类无穷小，它表明u与v趋向于0的速度是一致的，比如第一类重要极限：

注意，这时候并不是说sinx与x是相等的，它们还是有差距的，它们相差一个关于x的高阶无穷小：

再举两个例子。

• 例5

• 例6

这里，要注意的是，当x趋于0时，sinx与x，tanx与x都相差一个关于x的高阶无穷小，但是它们两个是不一样的。所以下面的逻辑是错误的：

关于x的两个无穷小量进行加减运算后，依然是关于x的无穷小量：

其次，有一类特殊的无穷小——任意阶数的x都是它的高阶无穷小，记为o(1)，举个例子：

2

在数列极限中，我们有下面不等式成立：

我们来看一个等价无穷大量的例子：

现在，我们来证明上一小节的极限。

3

• 三角函数等价量

• 对数函数等价量

• 指数函数等价量

• 幂函数等价量

最后，对于一些较简单的复合函数的等价量，记住一句口诀：无穷大量看高阶，无穷小量看低阶.先看两个例子

• 例7

• 例8

4

• 例9

• 例10

• 例11

• 例12

最后一个等式的形式，我们以后会重点研究，它就是著名的泰勒展开公式。这里先稍微带过。