大家好,欢迎来到IT知识分享网。
分布形态的度量-偏度系数与峰度系数的探讨
1.偏度系数
- 偏度(Skewnes)也称为偏态系数,是统计数据分布偏斜方向和程度的度量,是统计数据分布非对称程度的数字特征。在R软件中的计算公式如下:
S k e w n e s s = M 3 σ 3 = 1 n ∑ i = 1 n ( x i − x ˉ ) 3 σ 3 Skewness=\frac{M_3}{\sigma^{3}}=\frac{\frac{1}{n}\sum^{n}_{i=1}(x_i-\bar{x})^3}{\sigma^{3}} Skewness=σ3M3=σ3n1∑i=1n(xi−xˉ)3
偏度的作用:
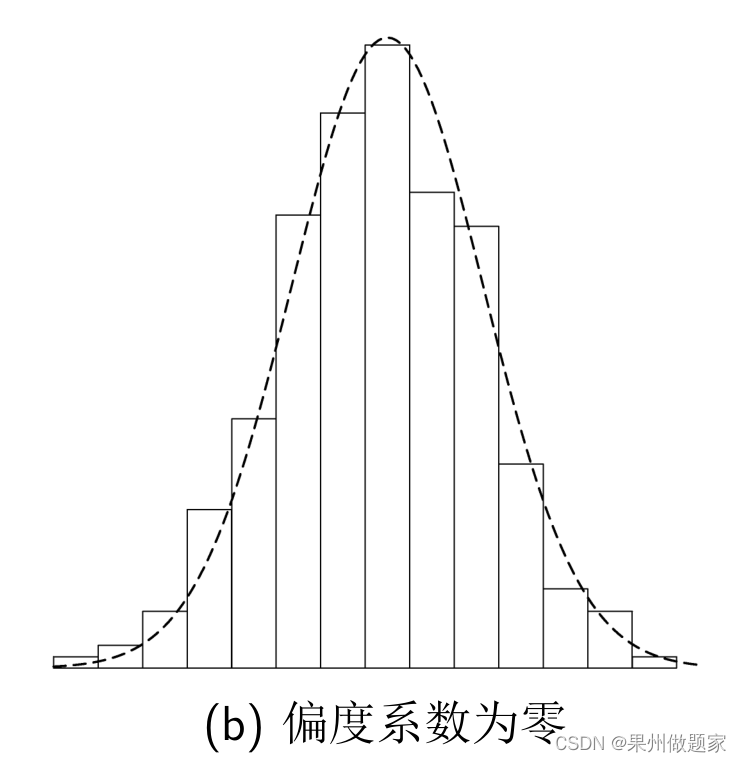
- 对于正态分布,其偏度为0,两侧尾部长度对称。此时:众数=中位数=平均数。
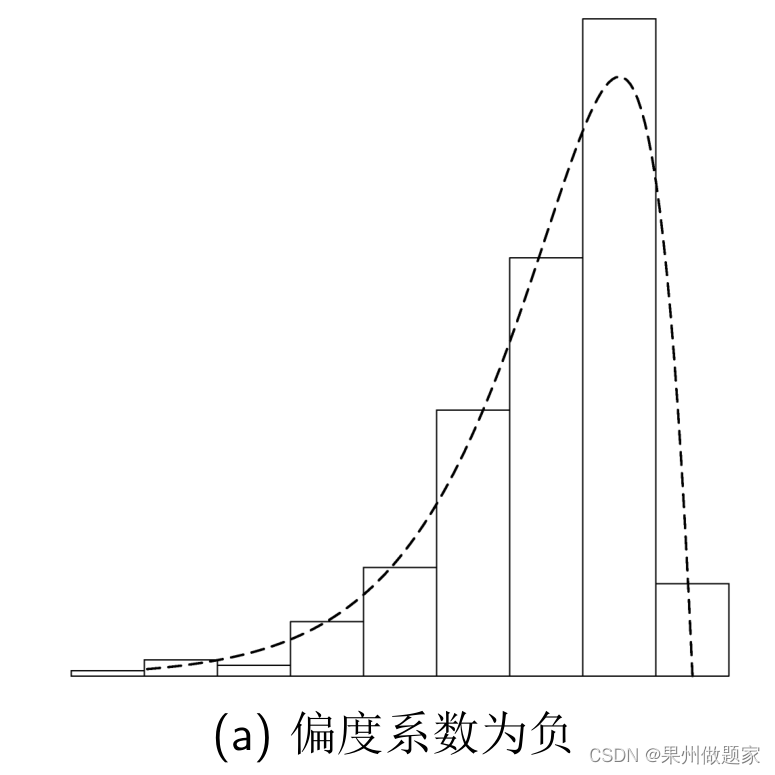
- 若分布的偏度小于0,则说明该分布具有负偏离,即左偏态,此时数据位于均值左边的比位于右边的少,直观表现为左边的尾部相对于与右边的尾部要长,因为有少数变量值很小,使曲线左侧尾部拖得很长。分布左偏时:众数>中位数>平均数。
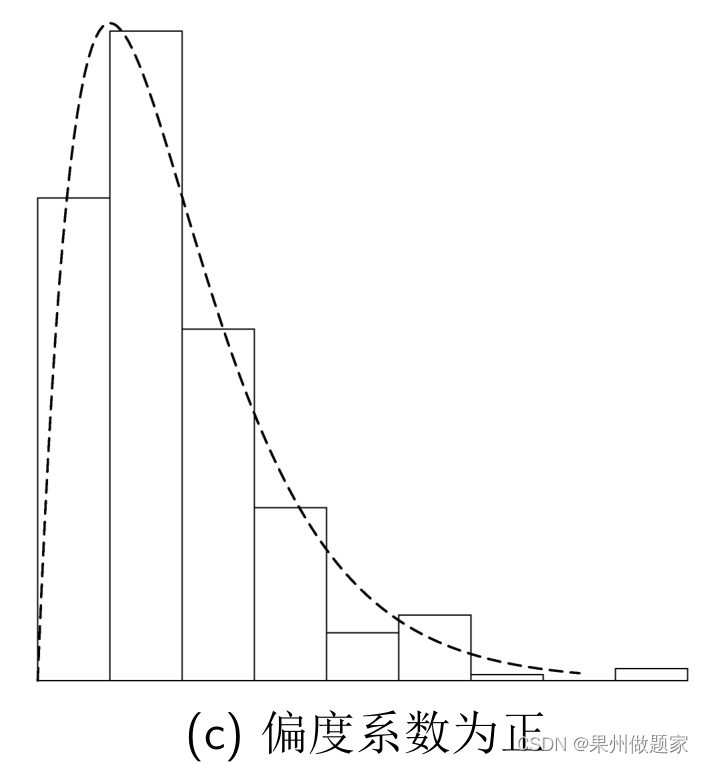
- 若分布的偏度大于0,即右偏态,此时数据位于均值右边的比位于左边的少,直观表现为右边的尾部相对于与左边的尾部要长,因为有少数变量值很大,使曲线右侧尾部拖得很长。分布右偏时:平均数>中位数>众数。
# 例1:为研究新生儿出生时的体重,在某妇产医院随机地选取了100个新生儿,其重量如表(数据存放在birth.csv文件中)。计算新生儿体重数据的偏度系数. birth<-read.table('data/birth.csv',header=TRUE,sep=',') head(birth,n=5) | x | |
|---|---|
| <int> | |
| 1 | 1740 |
| 2 | 3540 |
| 3 | 2760 |
| 4 | 3240 |
| 5 | 3960 |
自己编写计算偏度系数的函数:
skew<-function(x){ n<-length(x) ((1/n)*sum((x-mean(x))^3))/(sd(x)^3) } skew(birth$x) #偏度<0,说明数据是左侧更分散,属于左偏分布 -0.3803
使用e1071包里的偏度计算函数:
library(e1071) e1071::skewness(birth$x) #计算偏度系数 Warning message: "程辑包'e1071'是用R版本4.1.3 来建造的" -0.3803
使用timeDate包里的偏度计算函数:
timeDate::skewness(birth$x) #计算偏度系数 -0.3803
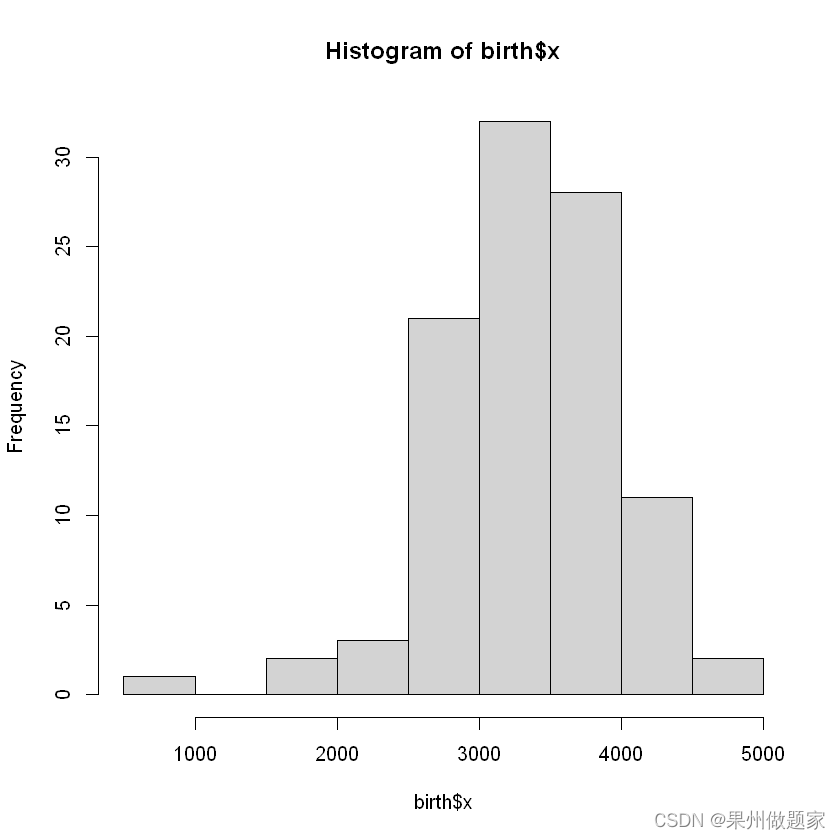
绘制直方图:
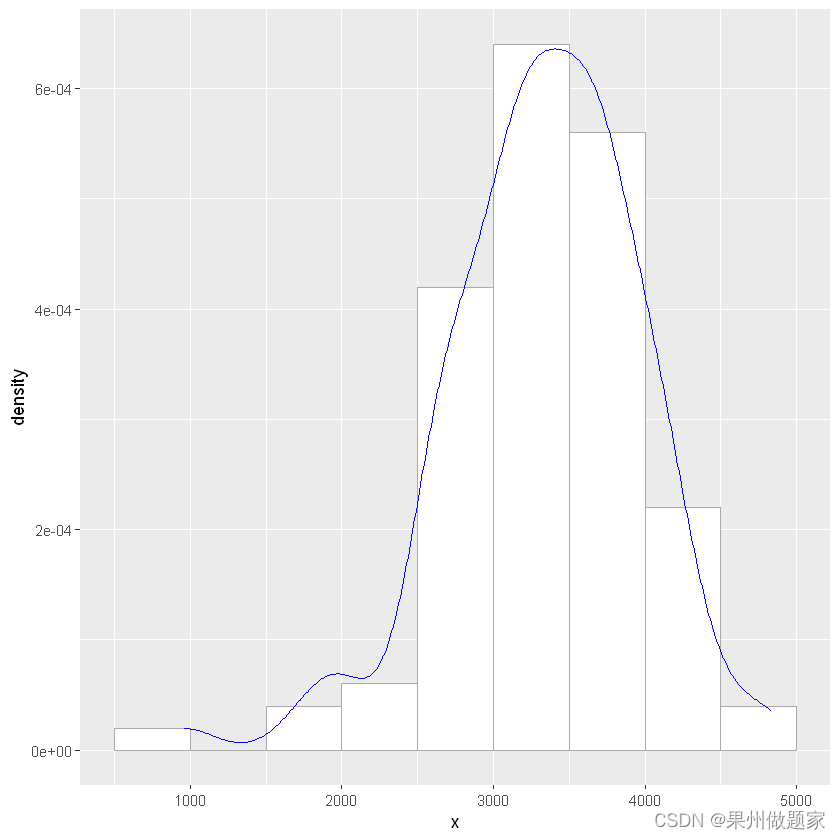
hist(birth$x) 使用ggplot2包绘制直方图和密度曲线:
library(ggplot2) #获取直方图相关参数 length_hist_results <- hist(birth$x,plot = FALSE) #绘制直方图 ggplot(data = birth, mapping = aes(x)) + geom_histogram( aes(y = ..density..), breaks = length_hist_results$breaks, color = "darkgray", fill = "white" ) + #绘制概率密度曲线 geom_density(colour = "blue") Warning message: "程辑包'ggplot2'是用R版本4.1.3 来建造的" 2.峰度系数
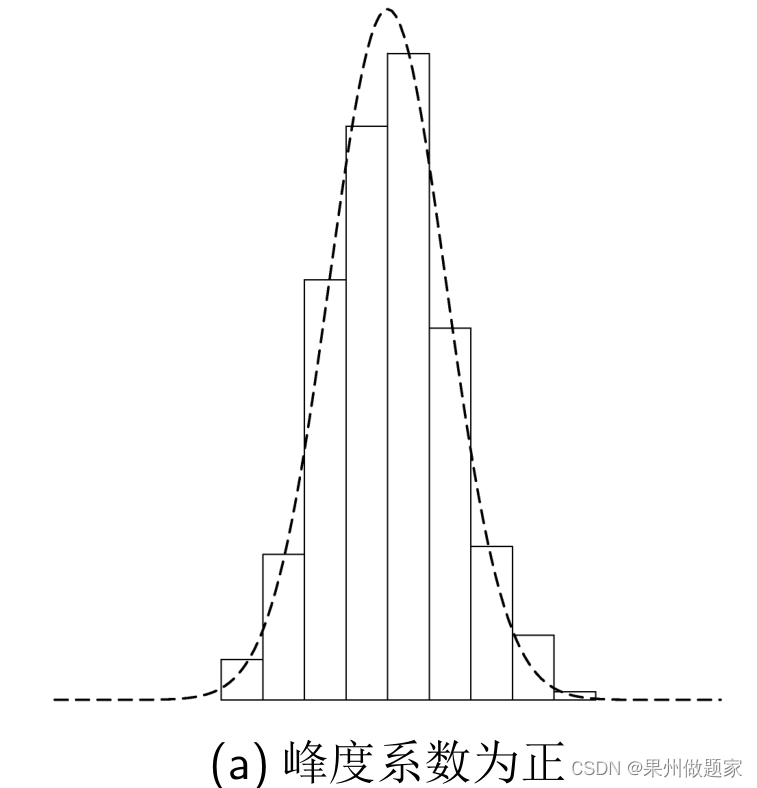
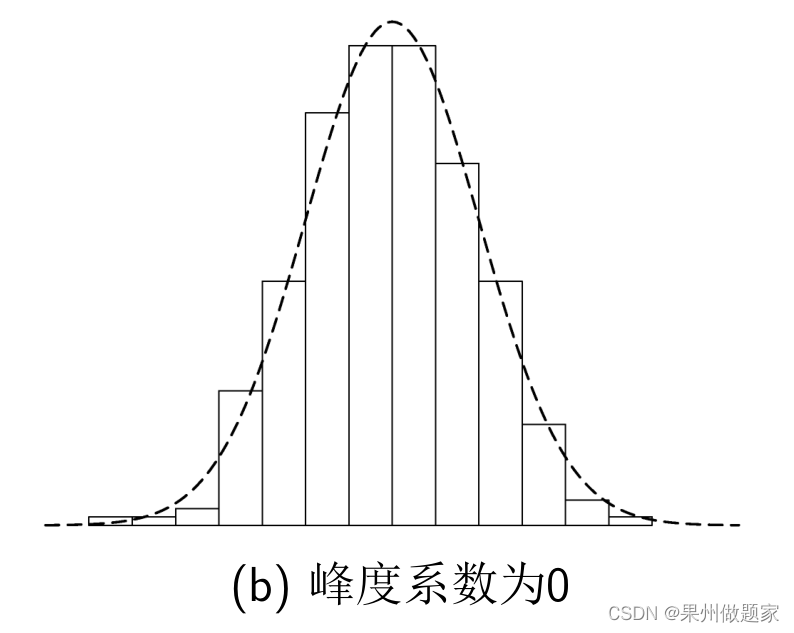
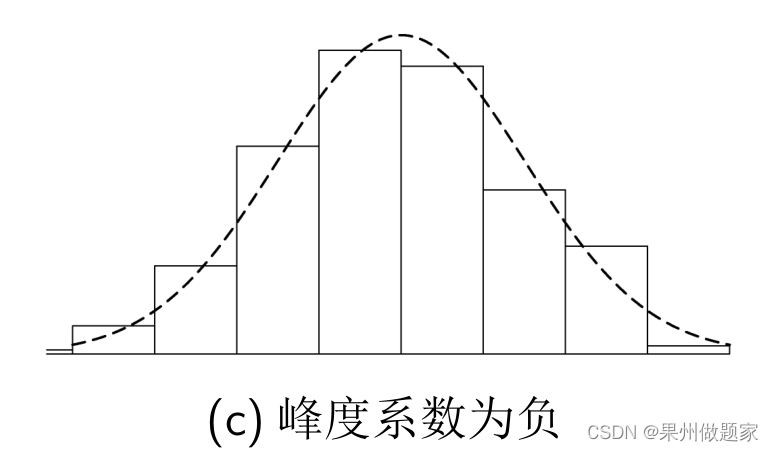
峰度系数反映分布峰的尖峭程度的重要指标.当峰度系数大于0时,两侧极端数据较多;当峰度系数小于0时,两侧极端数据较少。
峰度(kurtosis),又称峰态系数,是表征概率密度分布曲线在平均值处峰值高低的指标。直观地说,这个指标反映地是峰部的尖度。该指标的计算是相对于正态分布而言的(正态分布的峰度为0),如果峰度大于0,则说明峰的形状比较尖,比正态分布要陡峭。在统计学中,峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。对于具有n个值的样本,在R软件中的计算公式如下:
K u r t o s i s = M 4 σ 4 − 3 = 1 n ∑ i = 1 n ( x i − x ˉ ) 4 σ 4 − 3 Kurtosis=\frac{M_4}{\sigma^{4}}-3=\frac{\frac{1}{n}\sum^{n}_{i=1}(x_i-\bar{x})^4}{\sigma^{4}}-3 Kurtosis=σ4M4−3=σ4n1∑i=1n(xi−xˉ)4−3
# 自己编写的计算峰度系数的函数: kurt<-function(x){ n<-length(x) ((1/n)*sum((x-mean(x))^4))/(sd(x)^4)-3 } # 例1:为研究新生儿出生时的体重,在某妇产医院随机地选取了100个新生儿,其重量如表(数据存放在birth.csv文件中)。计算新生儿体重数据的峰度系数. birth<-read.table('data/birth.csv',header=TRUE,sep=',') kurt(birth$x) 1.776
使用e1071包里的峰度计算函数:
e1071::kurtosis(birth$x) #计算峰度系数 1.776
使用timeDate包里的峰度计算函数:
timeDate::kurtosis(birth$x) #计算峰度系数 1.776
教材例子验证
#代码3-5 通过psych包的describe()函数计算例3-2数据的描述性统计数 example3_2 <-read.table("swtj/Example3_2.csv", header=TRUE, sep=",") library(psych) psych::describe(example3_2)
| vars | n | mean | sd | median | trimmed | mad | min | max | range | skew | kurtosis | se | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <int> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | |
| x | 1 | 10 | 4.976 | 4.039508 | 4.165 | 4.80625 | 4.07715 | 0.3 | 11.01 | 10.71 | 0. | -1. | 1. |
| y | 2 | 10 | 109.000 | 61. | 118.500 | 110.62500 | 76.35390 | 25.0 | 180.00 | 155.00 | -0. | -1. | 19. |
“`R e1071::skewness(example3_2$x) #计算偏度系数 “`
0.3528
e1071::skewness(example3_2$y) #计算偏度系数 -0.8772
e1071::kurtosis(example3_2$x) #计算峰度系数 -1.354
e1071::kurtosis(example3_2$y) #计算峰度系数 -1.305
用自编函数计算,结果与R包函数计算结果完全相同:
skew(example3_2$x) #用自编函数计算偏度系数 0.3528
skew(example3_2$y) #用自编函数计算偏度系数 -0.8772
kurt(example3_2$x) #用自编函数计算峰度系数 -1.354
kurt(example3_2$y) #用自编函数计算峰度系数 -1.305
参考文献:
【1】薛毅,陈立萍.[M].R语言在统计中的应用.北京:中国工信出版集团,人民邮电出版社,2017.04.
【2】杨泽峰.[M].R语言在生物统计中的应用.南京:南京大学出版社,2022.02
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/134264.html