大家好,欢迎来到IT知识分享网。
在某些论文或文章里看到对数(等角)螺旋线的公式:
当然也有像我这样的想知道公式怎么推出了的,因此我写下这篇文章,希望能够帮助到大家。因本人才疏学浅,文章定有不足,希望大家能够在评论区讨论以及指正。
废话不多说,开启正文!
一、图形引入
下面是对数(等角)螺旋线的图片,可以清晰看出它的性质:图中曲线的在一任意点P处的切线与圆心O到这一点的连线所成角度α不变,也就是α是一个定值。
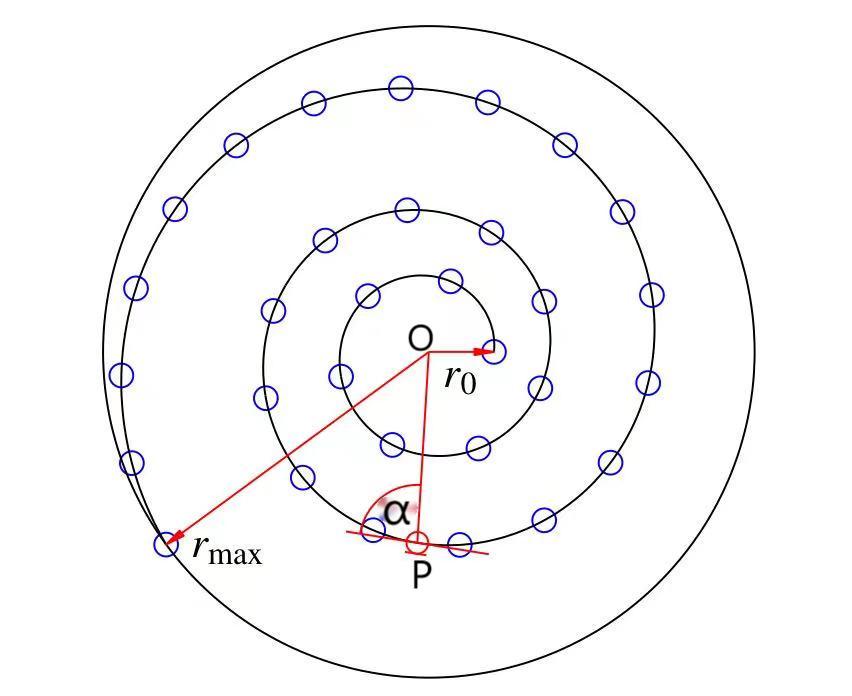
二、数学公式推导
- 若在极坐标系中,对数(等角)螺旋线的极坐标方程为:
,其中θ表示任意一点P的角度,因此该点极坐标为
。由推导可知该点的切向量为
切向量推导过程如下:
- 点P的极坐标为
,因此在直角坐标系中的坐标为
- 再分别对x,y轴坐标进行求导,
,
因此可得该点的切向量为:
- 因为α为该点的切向量与圆心连线的夹角,并且α是一个定值,这个角的大小永远不变,那么接下来就是要求出
这个定值,推导过程如下:
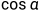
- 已知两向量的夹角公式为:
,
所以
- 对上式化简:
- 得到
的值后,继续求得
的值:

- 已知
可求得
,因为
所以,
- 已知
可得
,因为
所以,
- 继续求得最终对数(等角)螺旋线的极坐标方程:
极坐标方程推导如下:
- 已知
对上述式子两端积分可得,

- 化简上式,得到
- 所以,对数(等角)螺旋线的极坐标方程为:
,a为常数
三、性质
以上便是对数(等角)螺旋线极坐标方程的推导,根据公式:
对于每一个θ,都有一个r值相对应;当θ=0时,r=a,因此a可以影响螺旋线距离圆心的距离。其他的性质就不说那么多了,百度上很多讲性质的。
总结:打公式不易,如有错误欢迎指正!麻烦点赞收藏给个鼓励,谢谢~
最后再补充一张MATLAB实现的图吧!

免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/135154.html

 ,其中θ表示任意一点P的角度,因此该点极坐标为
,其中θ表示任意一点P的角度,因此该点极坐标为 。由推导可知该点的
。由推导可知该点的
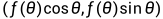
 ,
,

 ,
,




 ,因为
,因为




