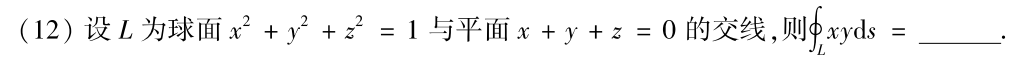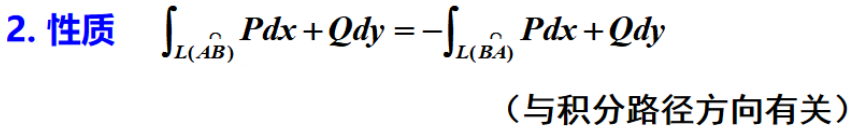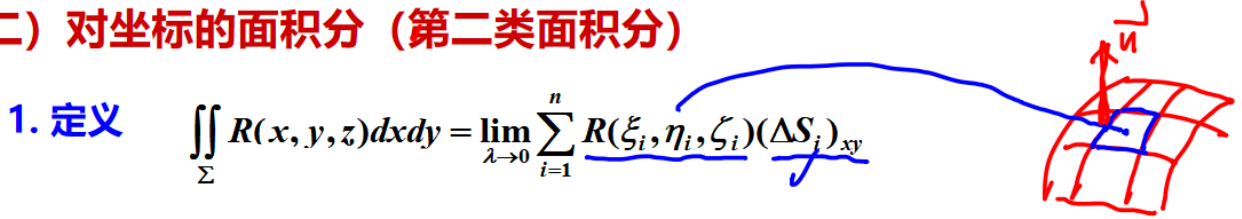大家好,欢迎来到IT知识分享网。
文章目录
Ch11. 曲线积分与曲面积分
零、代入法:线面积分可代,重积分(二重、三重)不可代入
一、曲线积分
(一) 第一类曲线积分:对弧长的曲线积分
1.定义
2.性质
第一类曲线积分,与路径方向无关: ∮ L ( A B ) f ( x , y ) d s = ∮ L ( B A ) f ( x , y ) d s \oint_{L(AB)}f(x,y)ds=\oint_{L(BA)}f(x,y)ds ∮L(AB)f(x,y)ds=∮L(BA)f(x,y)ds
3.应用:弧质量、曲线弧长
①弧长质量: m = ∮ L ρ ( x , y ) d s m=\oint_Lρ(x,y)ds m=∮Lρ(x,y)ds
②对1的第一类曲线积分,就是曲线的弧长: ∮ L 1 d s = L \oint_L1ds=L ∮L1ds=L
4.计算
(1)ds弧微分公式
①平面一类线
弧微分公式: d s = { 1 + y ′ 2 d x 一元函数 x ′ 2 ( t ) + y ′ 2 ( t ) d t 参数方程 ρ 2 ( θ ) + ρ ′ 2 ( θ ) d θ 极坐标 ds=\left\{\begin{aligned} \sqrt{1+y’^2}\ dx && 一元函数 \\ \sqrt{x’^2(t)+y’^2(t)}\ dt &&参数方程\\ \sqrt{ρ^2(θ)+ρ’^2(θ)}\ dθ &&极坐标 \end{aligned}\right. ds=⎩
⎨
⎧1+y′2 dxx′2(t)+y′2(t) dtρ2(θ)+ρ′2(θ) dθ一元函数参数方程极坐标
②空间一类线:化参数方程
设空间曲线L的方程为: x = x ( t ) , y = y ( t ) , z = z ( t ) ( α ≤ t ≤ β ) x=x(t),y=y(t),z=z(t) \uad (α≤t≤β) x=x(t),y=y(t),z=z(t)(α≤t≤β)
d s = x ′ 2 ( t ) + y ′ 2 ( t ) + z ′ 2 ( t ) d t ds=\sqrt{x’^2(t)+y’^2(t)+z’^2(t)}dt ds=x′2(t)+y′2(t)+z′2(t)dt
则 ∫ L f ( x , y , z ) d s = ∫ α β f [ x ( t ) , y ( t ) , z ( t ) ] ⋅ x ′ 2 ( t ) + y ′ 2 ( t ) + z ′ 2 ( t ) d t \int_Lf(x,y,z)ds=\int_α^βf[x(t),y(t),z(t)]·\sqrt{x’^2(t)+y’^2(t)+z’^2(t)}dt ∫Lf(x,y,z)ds=∫αβf[x(t),y(t),z(t)]⋅x′2(t)+y′2(t)+z′2(t)dt
(2)对称性:奇偶对称性(偶倍奇零)、轮换对称性
例题1:09年11. 定积分的计算:凑微分
答案: 13 6 \dfrac{13}{6} 613
分析: s = ∫ 0 π 4 1 + y ′ 2 ( x ) d x = ∫ 0 π 4 1 + t a n 2 x d x = ∫ 0 π 4 s e c 2 x d x = ln ∣ s e c x + t a n x ∣ ∣ 0 π 4 = ln ( 1 + 2 ) s=\int_0^{\frac{π}{4}}\sqrt{1+y’^2(x)}{\rm d}x=\int_0^{\frac{π}{4}}\sqrt{1+tan^2x}{\rm d}x=\int_0^{\frac{π}{4}}sec^2x{\rm d}x=\ln|secx+tanx||_0^{\frac{π}{4}}=\ln(1+\sqrt{2}) s=∫04π1+y′2(x)dx=∫04π1+tan2xdx=∫04πsec2xdx=ln∣secx+tanx∣∣04π=ln(1+2)
答案: ln ( 1 + 2 ) \ln(1+\sqrt{2}) ln(1+2)
例题3:24李林六(二)11. 一类线 + 变上限积分求导
答案: 2 3 π + 3 2 \dfrac{2}{3}π+\dfrac{\sqrt{3}}{2} 32π+23
例题4:18年12. 空间一类线:轮换对称性
答案: − π 3 -\dfrac{π}{3} −3π
例题5:24李林六(二) 14. 空间一类线:化参数方程
答案: π π π
(二) 第二类曲线积分:对坐标的曲线积分 ∫ L d x + d y + d z \int_Ldx+dy+dz ∫Ldx+dy+dz
1.定义
2.性质
3.几何意义:变力沿曲线所作的功
F ⃗ ( x , y ) = P ( x , y ) i ⃗ + Q ( x , y ) j ⃗ \vec{F}(x,y)=P(x,y)\vec{i}+Q(x,y)\vec{j} F(x,y)=P(x,y)i+Q(x,y)j
答案:5
4.两类曲线积分的联系
cos α d s = d x , cos β d s = d y \cosαds=dx,\cosβds=dy cosαds=dx,cosβds=dy,即 ∮ L ( P c o s α + Q c o s β ) d s = ∮ L P d x + Q d y \oint_L(Pcosα+Qcosβ)ds=\oint_L Pdx+Qdy ∮L(Pcosα+Qcosβ)ds=∮LPdx+Qdy
( cos α , cos β ) (\cosα,\cosβ) (cosα,cosβ):切线切向量的方向余弦
注意,α、β指曲线在点(x,y)处切向量的方向角
方向角:非零向量与三个坐标轴的夹角
5.计算
(1)平面线积分
步骤:
1.参数方程:化为定积分直接算
定理:设P(x,y)与Q(x,y)在有向曲线弧L上有定义且连续,L的参数方程为 { x = x ( t ) y = y ( t ) \left\{ \begin{aligned} x & = x(t) \\ y & = y(t) \end{aligned} \right. {
xy=x(t)=y(t)
则有 ∫ L P ( x , y ) d x + Q ( x , y ) d y = ∫ α β [ P ( x ( t ) , y ( t ) ) ⋅ x ′ ( t ) + Q ( x ( t ) , y ( t ) ) ⋅ y ′ ( t ) ] d t \int_LP(x,y)dx+Q(x,y)dy=\int_α^β[P(x(t), y(t))·x'(t)+Q(x(t), y(t))·y'(t)]dt ∫LP(x,y)dx+Q(x,y)dy=∫αβ[P(x(t),y(t))⋅x′(t)+Q(x(t),y(t))⋅y′(t)]dt
d x = d x d t d t , d y = d y d t d t dx=\dfrac{dx}{dt}dt,dy=\dfrac{dy}{dt}dt dx=dtdxdt,dy=dtdydt
2.格林公式
格林公式 定理1:设闭区域D由分段光滑的曲线L围成,若函数P(x,y)及Q(x,y)在D上具有一阶连续偏导数,则有
∮ L P d x + Q d y = ∬ D ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y \oint_LPdx+Qdy=\iint\limits_D(\frac{∂Q}{∂x}-\frac{∂P}{∂y})dxdy ∮LPdx+Qdy=D∬(∂x∂Q−∂y∂P)dxdy
其中,L是D的正向边界曲线。外逆内顺。
一元函数积分学中,牛顿-莱布尼茨公式 ∫ a b F ′ ( x ) d x = F ( b ) − F ( a ) \int_a^bF'(x)dx=F(b)-F(a) ∫abF′(x)dx=F(b)−F(a)
告诉我们:F’(x)在区间[a,b]上的积分,可以通过它的原函数F(x)在这个区间两个端点上的值来表达。 格林(Green)公式告诉我们,在平面区域D上的二重积分,可以通过沿闭区域D的边界曲线L上的曲线积分来表达。
①曲线不封闭,补线用格林
步骤里的最后一步(第4步),不封闭、不是积分与路径无关、直接算不好算,就需要补线用格林公式
②有奇点,要挖洞 (平面线积分)
2.步骤:
例如:计算 I = ∫ L x d y − y d x x 2 + y 2 I=\int_L\dfrac{xdy-ydx}{x^2+y^2} I=∫Lx2+y2xdy−ydx,L为逆时针
(1) I = ∫ L . . . I=\int_L… I=∫L…
令 P ( x , y ) = . . . , Q ( x , y ) = . . . P(x,y)=…,Q(x,y)=… P(x,y)=…,Q(x,y)=…
当 ( x , y ) ≠ ( 0 , 0 ) (x,y)≠(0,0) (x,y)=(0,0)时,有 ∂ Q ∂ x = . . . = ∂ P ∂ y \dfrac{∂Q}{∂x}=…=\dfrac{∂P}{∂y} ∂x∂Q=…=∂y∂P
(2)作辅助曲线 L 1 L_1 L1: 分母 = r 2 分母= r² 分母=r2 (r为充分小的正数),取逆/正时针方向。 (注意外逆内顺)
记 L 1 L_1 L1围成区域为 D 1 D_1 D1, L + L 1 L+L_1 L+L1围成区域 D\D₁
(3) I = ∮ L + L 1 − ∮ L 1 = I 0 − I 1 I=\oint_{L+L_1}-\oint_{L1}=I_0-I_1 I=∮L+L1−∮L1=I0−I1
I 0 = ∮ L + L 1 = 格林公式 ∬ D \ D 1 ( Q x − P y ) d x d y = 0 I_0=\oint_{L+L_1}\xlongequal{格林公式}\iint\limits_{D\backslash D_1}(Q_x-P_y)dxdy=0 I0=∮L+L1格林公式D\D1∬(Qx−Py)dxdy=0
I 1 = ∮ L 1 = 代入分母 1 r 2 ∮ L 1 . . . d x + . . . d y = 格林公式 1 r 2 ∬ D \ D 1 . . . d x d y = . . . I_1=\oint_{L_1}\xlongequal{代入分母}\dfrac{1}{r^2}\oint_{L_1}…dx+…dy\xlongequal{格林公式}\dfrac{1}{r^2}\iint\limits_{D\backslash D1}…dxdy=… I1=∮L1代入分母r21∮L1…dx+…dy格林公式r21D\D1∬…dxdy=…
∴ I = I 0 − I 1 = . . . I=I_0-I_1=… I=I0−I1=…
3.若PQ有一阶连续偏导数且 ∂ P ∂ x = ∂ Q ∂ y , ( x , y ) ≠ ( 0 , 0 ) \dfrac{∂P}{∂x}=\dfrac{∂Q}{∂y},(x,y)≠(0,0) ∂x∂P=∂y∂Q,(x,y)=(0,0),则有以下结论:【讲义P245 例4注】
1)沿任何一条不包含原点在内的分段光滑闭曲线的积分为零: I = 0 I=0 I=0
2)沿任何一条包含原点在内的分段光滑闭曲线的积分均相等:选以分母为边界的圆域或椭圆域进行积分。(即无论外面的D长啥样,最后都变成在L₁所围的D₁里积分。)
例题3:21年20. 平面二类线 + 有奇点,要打洞
(Ⅱ)有奇点,要打洞
总结:对比例5和例6,挖洞的积分值与外圈曲线围成的大小无关,只与①外圈曲线的方向有关(逆时针正,顺时针负) ②挖洞的形状大小有关 ③去掉分母后的 Q x − P y Q_x-P_y Qx−Py大小有关
答案:A
③曲线积分比较大小
对比可知, I 4 I_4 I4最大。
答案:D
3.平面上曲线积分与路径无关的充要条件:Qx = Py
P(x,y)、Q(x,y)在单连通区域D上有一阶连续偏导数,若 Qx = Py,则线积分与路径无关。
(1)改换路径
(2)利用原函数
求原函数的方法:①凑微分 ②偏积分
(2)空间线积分
1.参数方程
参数方程: { x = φ ( t ) y = ψ ( t ) z = ω ( t ) \left\{\begin{aligned} x & = φ(t) \\ y & = ψ(t) \\ z & = ω(t) \end{aligned}\right. ⎩
⎨
⎧xyz=φ(t)=ψ(t)=ω(t),则 ∫ L P d x + Q d y + R d z = ∫ α β [ P ⋅ φ ′ ( t ) + Q ⋅ ψ ′ ( t ) + R ⋅ ω ′ ( t ) ] d t \int_LPdx+Qdy+Rdz=\int_α^β[P·φ'(t)+Q·ψ'(t)+R·ω'(t)]dt ∫LPdx+Qdy+Rdz=∫αβ[P⋅φ′(t)+Q⋅ψ′(t)+R⋅ω′(t)]dt
2.斯托克斯公式
斯托克斯公式:封闭曲线积分 ⇦⇨ 围成的曲面积分
① ∮ Г P d x + Q d y + R d z = ∬ Σ ∣ c o s α c o s β c o s γ ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R ∣ d S \oint_ГPdx+Qdy+Rdz=\iint\limits_Σ\left|\begin{array}{ccc} cosα & cosβ & cosγ \\ \frac{∂}{∂x} & \frac{∂}{∂y} & \frac{∂}{∂z}\\ P&Q&R \end{array}\right|dS ∮ГPdx+Qdy+Rdz=Σ∬
cosα∂x∂Pcosβ∂y∂Qcosγ∂z∂R
dS
② ∮ Г P d x + Q d y + R d z = ∬ Σ ∣ d y d z d z d x d x d y ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R ∣ = ∬ Σ ( ∂ R ∂ y − ∂ Q ∂ z ) d y d z + ( ∂ P ∂ z − ∂ R ∂ x ) d z d x + ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y \oint_ГPdx+Qdy+Rdz=\iint\limits_Σ\left|\begin{array}{ccc} dydz & dzdx & dxdy\\ \frac{∂}{∂x} & \frac{∂}{∂y} & \frac{∂}{∂z}\\ P&Q&R \end{array}\right|=\iint\limits_Σ(\dfrac{∂R}{∂y}-\dfrac{∂Q}{∂z})dydz+(\dfrac{∂P}{∂z}-\dfrac{∂R}{∂x})dzdx+(\dfrac{∂Q}{∂x}-\dfrac{∂P}{∂y})dxdy ∮ГPdx+Qdy+Rdz=Σ∬
dydz∂x∂Pdzdx∂y∂Qdxdy∂z∂R
=Σ∬(∂y∂R−∂z∂Q)dydz+(∂z∂P−∂x∂R)dzdx+(∂x∂Q−∂y∂P)dxdy
例题1:11年12. 斜平面与圆柱截,都是椭圆。不需要认真画出图来,知道是个椭圆就行了。

答案:π
例题2:14年12. 三元空间曲线:①
参数方程 ②斯托克斯公式

答案:π
例题3:22年19. 空间二类线:斯托克斯公式Ⅱ型 + 高斯公式
分析:三元曲线积分:①补线段成封闭曲线用斯托克斯 ②把曲线L写成三元参数方程
(1)空间曲线积分与路径无关的充要条件:Ry=Qz,Pz=Rx,Qx=Py
即斯托克斯公式的三项均为0: ∂ R ∂ y = ∂ Q ∂ z , ∂ P ∂ z = ∂ R ∂ x , ∂ Q ∂ x = ∂ P ∂ y \dfrac{∂R}{∂y}=\dfrac{∂Q}{∂z},\dfrac{∂P}{∂z}=\dfrac{∂R}{∂x},\dfrac{∂Q}{∂x}=\dfrac{∂P}{∂y} ∂y∂R=∂z∂Q,∂z∂P=∂x∂R,∂x∂Q=∂y∂P
3.降维用格林:用z=z(x,y)消z
例题1:11年12. 法三 斜面切圆柱面,截面是椭圆,投影下来一定是圆(图都不需要认真画出来)
二、曲面积分
(一) 第一类曲面积分:对面积dS
1.定义
2.性质
3.几何意义、应用:曲面质量、曲面的面积
①曲面的质量: m = ∬ Σ ρ ( x , y , z ) d S m=\iint\limits_Σρ(x,y,z)dS m=Σ∬ρ(x,y,z)dS
②曲面的面积: S = ∬ Σ 1 d S S=\iint\limits_Σ1dS S=Σ∬1dS
4.计算
(1)求第一类曲面积分:直接法 (dS公式投影为二重积分)
①设曲面∑:z=z(x,y),(x,y)∈Dxy,则
∬ Σ f ( x , y , z ) d S = ∬ D x y f [ x , y , z ( x , y ) ] 1 + z x 2 ( x , y ) + z y 2 ( x , y ) d x d y \iint\limits_Σf(x,y,z){\rm d}S=\iint\limits_{D_{xy}}f[x,y,z(x,y)]\sqrt{1+z_x^2(x,y)+z_y^2(x,y)}{\rm d}x{\rm d}y Σ∬f(x,y,z)dS=Dxy∬f[x,y,z(x,y)]1+zx2(x,y)+zy2(x,y)dxdy
投影到xOy平面:(上下): d S = 1 + z x ′ 2 + z y ′ 2 d x d y dS=\sqrt{1+z_x’^2+z_y’^2}\ {\rm d}x{\rm d}y dS=1+zx′2+zy′2 dxdy
投影到yOz平面:(前后): d S = 1 + x y ′ 2 + x z ′ 2 d y d z dS=\sqrt{1+x_y’^2+x_z’^2}dydz dS=1+xy′2+xz′2dydz
③若曲面由方程y=y(x,z)给出,(x,z)∈Dxz,则
∬ Σ f ( x , y , z ) d S = ∬ D x z f [ x , y ( x , z ) , z ] 1 + y x 2 ( x , z ) + y z 2 ( x , z ) d x d z \iint\limits_Σf(x,y,z){\rm d}S=\iint\limits_{D_{xz}}f[x,y(x,z),z]\sqrt{1+y_x^2(x,z)+y_z^2(x,z)}{\rm d}x{\rm d}z Σ∬f(x,y,z)dS=Dxz∬f[x,y(x,z),z]1+yx2(x,z)+yz2(x,z)dxdz
投影到xOz平面:(左右): d S = 1 + y x ′ 2 + y z ′ 2 d x d z dS=\sqrt{1+y_x’^2+y_z’^2}dxdz dS=1+yx′2+yz′2dxdz
注:一类面投影为二重积分不考虑前面的正负
答案: 3 12 \dfrac{\sqrt{3}}{12} 123
例题3:23李林四20. 曲面的质量
答案:
(2)对称性:奇偶对称性、轮换对称性
答案: π 2 \dfrac{π}{2} 2π
(二) 第二类曲面积分:对坐标
1.定义
2.性质
3.应用:通量
4.计算
(1)曲线封闭,PQR一阶偏导存在:高斯公式
(2)曲线不封闭,直接算好算:直接法:①一投二代三定号 ②转换投影法(三合一公式)
(3)曲线不封闭,直接算不好算:补面用高斯公式
(1)高斯公式
历年真题:07、08年12、09、14、16、18年17.
①曲面封闭,直接用高斯公式
1.高斯公式 :封闭的第二类曲面积分→三重积分
设空间封闭区域Ω是由分片光滑的闭曲面Σ所围成,若函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在Ω上具有一阶连续偏导数,则有
∯ Σ P d y d z + Q d z d x + R d x d y = ∭ Ω ( ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z ) d v \oiint\limits_ΣPdydz+Qdzdx+Rdxdy=\iiint\limits_Ω(\dfrac{∂P}{∂x}+\dfrac{∂Q}{∂y}+\dfrac{∂R}{∂z}){\rm d}v Σ∬Pdydz+Qdzdx+Rdxdy=Ω∭(∂x∂P+∂y∂Q+∂z∂R)dv
这里Σ是Ω的整个边界曲面的外侧,cosα、cosβ与cosγ是Σ在点(x,y,z)处的法向量的方向余弦。
例题1:21年14. 外侧:已封闭,直接用高斯公式
分析:内侧、外侧是对已封闭曲面的说法,故封闭曲面可直接用高斯公式。再利用对称性、椭圆面积公式、柱体体积公式,可得 4 π 4π 4π
答案: 4 π 4π 4π
②曲面不封闭,补面用高斯公式
使用条件:PQR有连续一阶偏导,考虑补面为封闭空间区域,用高斯公式。
①曲面Σ有具体表达式,且没有分母,一般就可导
②要求可导,f只是连续函数无法使用高斯公式(如20年18题)
例题1:08年12. 对坐标的曲面积分、高斯公式(补辅助面)
分析:散度为y,考虑用高斯公式。曲面Σ不是封闭曲面,先补个面围成封闭曲面。
答案:4π
例题2:18年17. 第二类曲面积分 → 高斯公式 三重积分 → 截面法 二重积分 → 极坐标 定积分 第二类曲面积分\xrightarrow{高斯公式} 三重积分\xrightarrow[]{截面法}二重积分\xrightarrow[]{极坐标}定积分 第二类曲面积分高斯公式三重积分截面法二重积分极坐标定积分
③有奇点,先挖洞,再高斯公式: I = ∯ Σ = ∯ Σ + Σ 1 − ∯ Σ 1 I=\oiint\limits_Σ=\oiint\limits_{Σ+Σ_1}-\oiint\limits_{Σ_1} I=Σ∬=Σ+Σ1∬−Σ1∬
例1:09年19题
例2:辅导讲义P252例3
(2)直接法
①一投二代三定号
②转换投影法 (三合一公式)
将对曲面的曲面积分,投影到某个坐标面上,变为对该坐标面的二重积分
①投影到xOy平面: ∬ Σ P d y d z + Q d z d x + R d x d y = ∬ Σ [ P ⋅ ( − z x ) + Q ⋅ ( − z y ) + R ] d x d y = ± ∬ D x y [ P ⋅ ( − z x ) + Q ⋅ ( − z y ) + R ] d x d y (上侧取正 , 下侧取负) \iint\limits_ΣPdydz+Qdzdx+Rdxdy=\iint\limits_Σ[P·(-z_x)+Q·(-z_y)+R]dxdy=±\iint\limits_{D_{xy}}[P·(-z_x)+Q·(-z_y)+R]dxdy(上侧取正,下侧取负) Σ∬Pdydz+Qdzdx+Rdxdy=Σ∬[P⋅(−zx)+Q⋅(−zy)+R]dxdy=±Dxy∬[P⋅(−zx)+Q⋅(−zy)+R]dxdy(上侧取正,下侧取负)
②投影到xOz平面: ∬ Σ P d y d z + Q d z d x + R d x d y = ± ∬ D y z [ P ⋅ ( − y x ) + Q + R ⋅ ( − y z ) ] d z d x (右侧取正 , 左侧取负) \iint\limits_ΣPdydz+Qdzdx+Rdxdy=±\iint\limits_{D_{yz}}[P·(-y_x)+Q+R·(-y_z)]dzdx(右侧取正,左侧取负) Σ∬Pdydz+Qdzdx+Rdxdy=±Dyz∬[P⋅(−yx)+Q+R⋅(−yz)]dzdx(右侧取正,左侧取负)
③投影到yOz平面: ∬ Σ P d y d z + Q d z d x + R d x d y = ± ∬ D x z [ P + Q ⋅ ( − x y ) + R ⋅ ( − x z ) ] d y d z (前侧取正 , 后侧取负) \iint\limits_ΣPdydz+Qdzdx+Rdxdy=±\iint\limits_{D_{xz}}[P+Q·(-x_y)+R·(-x_z)]dydz(前侧取正,后侧取负) Σ∬Pdydz+Qdzdx+Rdxdy=±Dxz∬[P+Q⋅(−xy)+R⋅(−xz)]dydz(前侧取正,后侧取负)
两类曲面积分之间的联系:化二型面为一型面
∬ Σ P d y d z + Q d z d x + R d x d y = ∬ Σ ( P cos α + Q cos β + R cos γ ) d S d y d z = cos α d S , d z d x = cos β d S , d x d y = cos γ d S \iint\limits_ΣPdydz+Qdzdx+Rdxdy=\iint\limits_Σ(P\cosα+Q\cosβ+R\cosγ)dS\\[5mm] dydz=\cosα{\rm d}S,dzdx=\cosβ{\rm d}S,dxdy=\cosγ{\rm d}S Σ∬Pdydz+Qdzdx+Rdxdy=Σ∬(Pcosα+Qcosβ+Rcosγ)dSdydz=cosαdS,dzdx=cosβdS,dxdy=cosγdS
( cos α , cos β , cos γ ) (\cosα,\cos β,\cos γ) (cosα,cosβ,cosγ)为曲面的法向量的方向余弦,即单位化的法向量
用 两类曲面积分之间的联系 推导出 转换投影法(三合一公式):都提一个cosγ出去
例题1:20年18. 不可导无法使用高斯公式,消去抽象函数:两类曲面积分之间的联系,化二型面为一型面 或 转换投影法 【辅导讲义P252例5】
例题2:24李林六(一) PQR有奇点,不可导。不能用高斯公式,只能用转换投影法
例题3:19年12. 开根要带绝对值、 ∣ y ∣ |y| ∣y∣是关于y的偶函数
分析:曲线曲面积分,可以用代入法。开根要带绝对值。
答案: 32 3 \dfrac{32}{3} 332
例题4:06年3. 补面 + 高斯公式 +投影 + 代入z=1
分析:
①补面 Σ ′ : z = 1 ( x 2 + y 2 ≤ 1 ) Σ’ :z=1\ (x²+y²≤1) Σ′:z=1 (x2+y2≤1)
②高斯公式得封闭曲面积分为6倍圆锥体积= 2 π 2π 2π
③ ∬ Σ ′ x d y d z + 2 y d z d x + 3 ( z − 1 ) d x d y = + ∬ D x y 3 ( z − 1 ) d x d y \iint\limits_{Σ’}xdydz+2ydzdx+3(z-1)dxdy=+\iint\limits_{Dxy}3(z-1)dxdy Σ′∬xdydz+2ydzdx+3(z−1)dxdy=+Dxy∬3(z−1)dxdy
④由于补面 Σ ′ 为 z = 1 ( x 2 + y 2 ≤ 1 ) Σ’ 为z=1\ (x²+y²≤1) Σ′为z=1 (x2+y2≤1),所以z-1=0,所以代入得该积分为0
⑤相减, 2 π − 0 = 2 π 2π-0=2π 2π−0=2π
答案: 2 π 2π 2π
三、多元积分的应用
1.面积、体积、质量、质心、形心坐标、转动惯量
| 平面薄片 (二重积分) | 空间体 (三重积分) | 曲线 (一类线积分) | 曲面 (一类面积分) | |
|---|---|---|---|---|
| (1)几何度量 | ①平面面积: S = ∬ D 1 d σ S=\iint\limits_D1dσ S=D∬1dσ ②曲顶柱体体积: V = ∬ D f ( x , y ) d σ V=\iint\limits_D f(x,y)dσ V=D∬f(x,y)dσ |
空间体积: V = ∭ V 1 d v V=\iiint\limits_V1dv V=V∭1dv | 曲线弧长: s = ∫ L 1 d s s=\int_L1ds s=∫L1ds | 曲面面积: S = ∬ Σ 1 d S S=\iint\limits_Σ1dS S=Σ∬1dS |
| (2)质量 | 平面板质量: m = ∬ D ρ ( x , y ) d σ m=\iint\limits_Dρ(x,y)dσ m=D∬ρ(x,y)dσ | 空间体质量: m = ∭ V ρ ( x , y , z ) d v m=\iiint\limits_Vρ(x,y,z)dv m=V∭ρ(x,y,z)dv | 曲线弧质量: m = ∫ L ρ ( x , y ) d σ m=\int_Lρ(x,y)dσ m=∫Lρ(x,y)dσ | 曲面质量: m = ∬ Σ ρ ( x , y , z ) d S m=\iint\limits_Σρ(x,y,z)dS m=Σ∬ρ(x,y,z)dS |
| (3)质心( x ˉ , y ˉ , z ˉ \bar{x},\bar{y},\bar{z} xˉ,yˉ,zˉ) | x ˉ = ∬ D x ρ ( x , y ) d σ ∬ D ρ ( x , y ) d σ \bar{x}=\dfrac{\iint\limits_Dxρ(x,y)dσ}{\iint\limits_Dρ(x,y)dσ} xˉ=D∬ρ(x,y)dσD∬xρ(x,y)dσ | x ˉ = ∭ V x ρ ( x , y , z ) d v ∭ V ρ ( x , y , z ) d v \bar{x}=\dfrac{\iiint\limits_Vxρ(x,y,z)dv}{\iiint\limits_Vρ(x,y,z)dv} xˉ=V∭ρ(x,y,z)dvV∭xρ(x,y,z)dv | x ˉ = ∫ L x ρ ( x , y ) d σ ∫ L ρ ( x , y ) d σ \bar{x}=\dfrac{\int_Lxρ(x,y)dσ}{\int_Lρ(x,y)dσ} xˉ=∫Lρ(x,y)dσ∫Lxρ(x,y)dσ | x ˉ = ∬ Σ x ρ ( x , y , z ) d S ∬ Σ ρ ( x , y , z ) d S \bar{x}=\dfrac{\iint\limits_Σxρ(x,y,z)dS}{\iint\limits_Σρ(x,y,z)dS} xˉ=Σ∬ρ(x,y,z)dSΣ∬xρ(x,y,z)dS |
| 形心坐标(ρ=1) | x ˉ = ∬ D x d S S \bar{x}=\dfrac{\iint\limits_DxdS}{S} xˉ=SD∬xdS (S为积分区域D的面积) |
x ˉ = ∭ Ω x d v V \bar{x}=\dfrac{\iiint\limits_Ωxdv}{V} xˉ=VΩ∭xdv (V为积分区域Ω的体积) |
x ˉ = ∮ x d s l \bar{x}=\dfrac{\oint xds}{l} xˉ=l∮xds ( l l l为曲线长度) |
x ˉ = ∬ Σ x d S S \bar{x}=\dfrac{\iint\limits_ΣxdS}{S} xˉ=SΣ∬xdS (S为曲面表面积) |
| (4)转动惯量( I x , I y , I z I_x,I_y,I_z Ix,Iy,Iz) | ① I x = ∬ D y 2 ρ ( x , y ) d σ I_x=\iint\limits_Dy^2ρ(x,y)dσ Ix=D∬y2ρ(x,y)dσ ② I y = ∬ D x 2 ρ ( x , y ) d σ I_y=\iint\limits_Dx^2ρ(x,y)dσ Iy=D∬x2ρ(x,y)dσ |
① I x = ∭ Ω ( y 2 + z 2 ) ρ ( x , y , z ) d v I_x=\iiint\limits_Ω(y^2+z^2)ρ(x,y,z)dv Ix=Ω∭(y2+z2)ρ(x,y,z)dv ② I y = ∭ Ω ( x 2 + z 2 ) ρ ( x , y , z ) d v I_y=\iiint\limits_Ω(x^2+z^2)ρ(x,y,z)dv Iy=Ω∭(x2+z2)ρ(x,y,z)dv ③ I z = ∭ Ω ( x 2 + y 2 ) ρ ( x , y , z ) d v I_z=\iiint\limits_Ω(x^2+y^2)ρ(x,y,z)dv Iz=Ω∭(x2+y2)ρ(x,y,z)dv |
1.变力做功: W = ∫ A B P d x + Q d y + R d z W=\int_{AB}Pdx+Qdy+Rdz W=∫ABPdx+Qdy+Rdz
2.通量: Φ = ∬ Σ P d y d z + Q d z d x + R d x d y Φ=\iint\limits_ΣPdydz+Qdzdx+Rdxdy Φ=Σ∬Pdydz+Qdzdx+Rdxdy
(1)形心坐标
ρ(x,y,z)=1时质心,称为形心 (质地均匀,密度为常量)
求二维、三维质心、形心,注意对称性:关于x轴、yOz面对称则 y ˉ = 0 \bar{y}=0 yˉ=0;关于y轴对称则 x ˉ = 0 \bar{x}=0 xˉ=0
平面形心 (二维均匀薄面的形心坐标): 二重积分的计算
x ˉ = ∬ D x d σ A , y ˉ = ∬ D y d σ A \bar{x}=\frac{\iint\limits_Dx{\rm d}σ}{A},\bar{y}=\frac{\iint\limits_Dy{\rm d}σ}{A} xˉ=AD∬xdσ,yˉ=AD∬ydσ
A = ∬ D d σ A=\iint\limits_D{\rm d}σ A=D∬dσ
空间体形心(三维密度均匀的几何体的形心坐标): 三重积分的计算、二次曲面
x ˉ = ∭ Ω x d v V , y ˉ = ∭ Ω y d v V , z ˉ = ∭ Ω z d v V \bar{x}=\frac{\iiint\limits_Ωx{\rm d}v}{V},\bar{y}=\frac{\iiint\limits_Ωy{\rm d}v}{V},\bar{z}=\frac{\iiint\limits_Ωz{\rm d}v}{V} xˉ=VΩ∭xdv,yˉ=VΩ∭ydv,zˉ=VΩ∭zdv
V = ∭ Ω d v = ∭ Ω d x d y d z V=\iiint\limits_Ω{\rm d}v=\iiint\limits_Ω{\rm d}x{\rm d}y{\rm d}z V=Ω∭dv=Ω∭dxdydz
例题1:10年12. 重积分的应用:形心坐标
分析: z ˉ = ∭ Ω z d v ∭ Ω d v \bar{z}=\dfrac{\iiint\limits_Ωz{\rm d}v}{\iiint\limits_Ω{\rm d}v} zˉ=Ω∭dvΩ∭zdv
被积函数只有z,考虑截面法:截面面积为 πρ² = πz
∭ Ω z d v = ∫ 0 1 d z ∬ D z z d x d y = ∫ 0 1 z ⋅ π z d z = π ∫ 0 1 z 2 d z = π 3 \iiint\limits_Ωz{\rm d}v=\int_{0}^{1}dz\iint\limits_{D_z}z{\rm d}x{\rm d}y=\int_{0}^{1}z·πzdz=π\int_{0}^{1}z^2dz=\dfrac{π}{3} Ω∭zdv=∫01dzDz∬zdxdy=∫01z⋅πzdz=π∫01z2dz=3π
∭ Ω d v = ∫ 0 1 d z ∬ D z d x d y = ∫ 0 1 π z d z = π ∫ 0 1 z d z = π 2 \iiint\limits_Ω{\rm d}v=\int_0^1dz\iint\limits_{D_z}{\rm d}x{\rm d}y=\int_0^1πzdz=π\int_0^1zdz=\dfrac{π}{2} Ω∭dv=∫01dzDz∬dxdy=∫01πzdz=π∫01zdz=2π
∴ z ˉ = ∭ Ω z d v ∭ Ω d v = π 3 π 2 = 2 3 ∴\bar{z}=\dfrac{\iiint\limits_Ωz{\rm d}v}{\iiint\limits_Ω{\rm d}v}=\dfrac{\dfrac{π}{3}}{\dfrac{π}{2}}=\dfrac{2}{3} ∴zˉ=Ω∭dvΩ∭zdv=2π3π=32
答案: 2 3 \dfrac{2}{3} 32
例题2:24李林四(一)13. 质心坐标
分析:
答案: 2 3 \dfrac{2}{3} 32
例题3:13年19. 重积分的应用:形心坐标
例题4:19年19. 【高数辅导讲义P256例3】 三重积分的几何应用:形心坐标、对称性
(1)将 x x x换成 − x -x −x,锥面方程不变 ∴锥面、锥体关于 y O z yOz yOz面对称
由对称性知 x ‾ = 0 \overline{x}=0 x=0
(3) V 锥体 = 1 3 S h = 1 3 × π × 1 2 × 1 = π 3 V_{锥体}=\dfrac{1}{3}Sh=\dfrac{1}{3}×π×1^2×1=\dfrac{π}{3} V锥体=31Sh=31×π×12×1=3π
(4)先二后一,求 ∭ Ω z d v \iiint\limits_Ωzdv Ω∭zdv:截面法,得 π 12 \dfrac{π}{12} 12π
(5)先二后一,求 ∭ Ω y d v \iiint\limits_Ωydv Ω∭ydv:
①方法一(标准答案):平移 + 极坐标,令x=ρcosθ,y-z=ρsinθ,即y=z+ρsinθ。运算量略大
②方法二(武忠祥):奇函数的平移 y=y-z+z,而y-z关于平面对称,又是y-z的奇函数,故积分为0,只剩z的三重积分,上问求过了,是 π 12 \dfrac{π}{12} 12π
(6)代入得出形心坐标 ( x ‾ , y ‾ , z ‾ ) (\overline{x},\overline{y},\overline{z}) (x,y,z)
答案: ( 0 , 1 4 , 1 4 ) (0,\dfrac{1}{4},\dfrac{1}{4}) (0,41,41)
分析:建立坐标,令P₀位于原点,则密度函数 ρ ( x , y , z ) = k ( x 2 + y 2 + z 2 ) ρ(x,y,z)=k(x^2+y^2+z^2) ρ(x,y,z)=k(x2+y2+z2)
(2)转动惯量
答案:2π
答案:2π
2.利用形心公式 求解线面积分、重积分
1.若已知形心坐标 x ˉ \bar{x} xˉ、曲面面积S,则 ∬ Σ x d S = x ˉ ⋅ S \iint\limits_Σ xdS=\bar{x}·S Σ∬xdS=xˉ⋅S
3.重积分、线面积分的最值问题
答案:8π
答案: − 8 5 π -\dfrac{8}{5}π −58π
答案: 3 2 π \dfrac{3}{2}π 23π
四、场论初步
1.方向导数
2.梯度
3.散度 divA
散度是一个数,出自高斯公式:
若向量 A = P i ⃗ + Q j ⃗ + R k ⃗ \boldsymbol A=P\vec{i}+Q\vec{j}+R\vec{k} A=Pi+Qj+Rk,则散度:
d i v A = ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z div A = \dfrac{∂P}{∂x}+ \dfrac{∂Q}{∂y}+ \dfrac{∂R}{∂z} divA=∂x∂P+∂y∂Q+∂z∂R
4.旋度 rot A
旋度是一个向量,出自斯托克斯公式:
设有一向量场 F ( x , y , z ) = P ( x , y , z ) i ⃗ + Q ( x , y , z ) j ⃗ + R ( x , y , z ) k ⃗ F(x,y,z)=P(x,y,z)\vec{i}+Q(x,y,z)\vec{j}+R(x,y,z)\vec{k} F(x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k
旋度, r o t F = ∣ i ⃗ j ⃗ k ⃗ ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R ∣ = ( ∂ R ∂ y − ∂ Q ∂ z ) i ⃗ + ( ∂ P ∂ z − ∂ R ∂ x ) j ⃗ + ( ∂ Q ∂ x − ∂ P ∂ y ) k ⃗ rotF=\left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ \frac{∂}{∂x} & \frac{∂}{∂y} & \frac{∂}{∂z}\\ P&Q&R \end{array}\right|=(\dfrac{∂R}{∂y}-\dfrac{∂Q}{∂z})\vec{i}+(\dfrac{∂P}{∂z}-\dfrac{∂R}{∂x})\vec{j}+(\dfrac{∂Q}{∂x}-\dfrac{∂P}{∂y})\vec{k} rotF=
i∂x∂Pj∂y∂Qk∂z∂R
=(∂y∂R−∂z∂Q)i+(∂z∂P−∂x∂R)j+(∂x∂Q−∂y∂P)k
分析: r o t F = ∣ i ⃗ j ⃗ k ⃗ ∂ ∂ x ∂ ∂ y ∂ ∂ z x y − y z z x ∣ = 0 − ( x k ⃗ − y i ⃗ + z j ⃗ ) rotF=\left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ \frac{∂}{∂x} & \frac{∂}{∂y} & \frac{∂}{∂z}\\ xy&-yz&zx \end{array}\right|=0-(x\vec{k}-y\vec{i}+z\vec{j}) rotF=
i∂x∂xyj∂y∂−yzk∂z∂zx
=0−(xk−yi+zj) 代入(1,1,0) 得 − ( k ⃗ − i ⃗ ) = i ⃗ − k ⃗ -(\vec{k}-\vec{i})=\vec{i}-\vec{k} −(k−i)=i−k
答案: i ⃗ − k ⃗ \vec{i}-\vec{k} i−k
答案: j ⃗ + ( y − 1 ) k ⃗ \vec{j}+(y-1)\vec{k} j+(y−1)k
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/136058.html