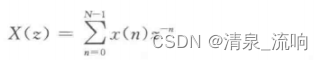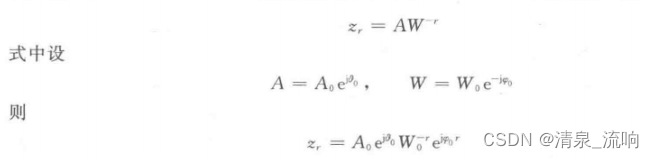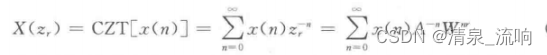大家好,欢迎来到IT知识分享网。
已知有限长序列x(n)的Z变换为
由上式中可知z=e^(s*Ts)=e^(a+jΩ)Ts=e^(a*Ts)*e^(jΩTs)=Ae^(jΩ*Ts),,s为拉普拉斯变量,A=e^(aTs)为实数,w=ΩTs,为一角度(角频率),现在对上式z的表示进行修改,令
A。、W。为任意的正实数,给定A。、W。、θ。、φ。当r=0,1,…,∞时,可以得到z平面上的一个个点z0,z1,…,z∞,取这些点上的Z变换有
这就是线性调频Z变换(CZT)的定义。
做CZT时在单位圆上取的频率刻度间隔可以小于DFT时的频率间隔,这样是否可以细化频谱?只有满足一定的条件才能细化频谱,但不是能无条件地任意细化频谱。
不同窗函数对应的CZT不发生比较严重谱线干涉现象的最小频率间隔
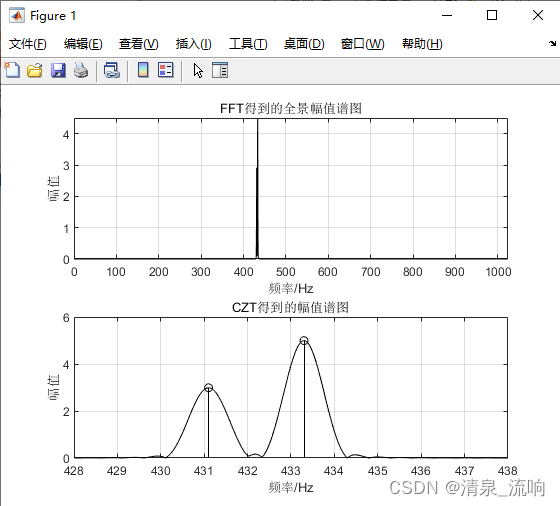
案例、设信号由两个正弦信号组成,频率分别为431.1Hz和433.3Hz,幅值分别为3和5,采样频率为2048Hz,数据长为4096。用FFT和CZT分别处理该信号并进行比较。程序如下:
clear all; clc; close all; fs=2048; % 采样频率 N=4096; % 信号长度 df1=fs/N; % 分辨率 n=1:N; % 样点索引 t=(n-1)/fs; % 时间序列 f1=431.1; f2=433.3; % 信号频率 s=3*cos(2*pi*f1*t)+5*cos(2*pi*f2*t-0.4); % 构成信号序列 wind=hanning(N)'; % 窗函数 S=abs(fft(s.*wind))*4/N; % FFT并求幅值 n1=1:N/2; % 正频率部分索引 fre1=(n1-1)*fs/N; % FFT变换后的正频率刻度 [K,V]=findpeakm(S(n1),'minpeakheight',1); % 寻找FFT频谱幅值的峰值并显示 fprintf('%5.2f %5.2f %5.2f %5.2f\n',fre1(K(1)),V(1),fre1(K(2)),V(2)) % CZT f0=428; DELf=0.01; M=N/4; % 设置CZT的参数f0,DELf和M n2=f0:DELf:f0+(M-1)*DELf; % 设置CZT中的频率区间 A=exp(1j*2*pi*f0/fs); % 设置A和W W=exp(-1j*2*pi*DELf/fs); G=czt(s.*wind,M,W,A); % CZT变换 GX=abs(G)*4/N; % 求出CZT后的频谱幅值 [K,V]=findpeakm(GX,'minpeakheight',1); % 寻找CZT频谱幅值的峰值并显示 fprintf('%5.2f %5.2f %5.2f %5.2f\n',n2(K(1)),V(1),n2(K(2)),V(2)) % 作图 subplot 211; plot((n1-1)*df1,S(n1),'k'); title('FFT得到的全景幅值谱图') xlabel('频率/Hz'); ylabel('幅值'); grid on; xlim([0 fs/2]) subplot 212; plot(n2,abs(GX),'k'); title('CZT得到的幅值谱图') xlabel('频率/Hz'); ylabel('幅值'); grid on; xlim([428 438]); hold on stem(n2(K(5)),V(5),'k'); stem(n2(K(7)),V(7),'k'); set(gcf,'color','w');运行结果如下:
虽然我们也把CZT说成是细化分析,但CZT和ZFFT本质是不同的,ZFFT是把发生干涉的频率成分先拉开再细化,而CZT只是对分析频带的局部放大。因此,对于发生严重干涉现象的频率成分的分离能力是有很大差别的:ZFFT经增大细化倍数、滤波和重抽样后能分离出不同频率成分;而CZT对谱峰重叠一起时是无法分离的。这告诉我们,在使用CZT时需要特别注意(同时也应注意到使用CZT和ZFFT时原始数据长度是不同的)。
参考文献:MATLAB数字信号处理85个实用案例精讲——入门到进阶;宋知用(编著)
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/137365.html