关于叉积公式的推导

大家好，欢迎来到IT知识分享网。

前言

在我看到过的大学线性代数教材中，都是直接给出向量积的定义和公式，有的可能给出了和行列式的关联，但是，向量的公式是可以通过它的几何意义推出的，最近我就尝试着推出了这个公式，写在这里。

前置知识

在阅读本文前，你需要了解以下知识：

1. 向量的基本概念
2. 向量内积（点积）的基本概念
3. 对线性代数的初步了解

基本定义

叉积，即外积、向量积。

向量$\vec{a}$和向量$\vec{b}$的叉积记作$\vec{a}\times \vec{b}$

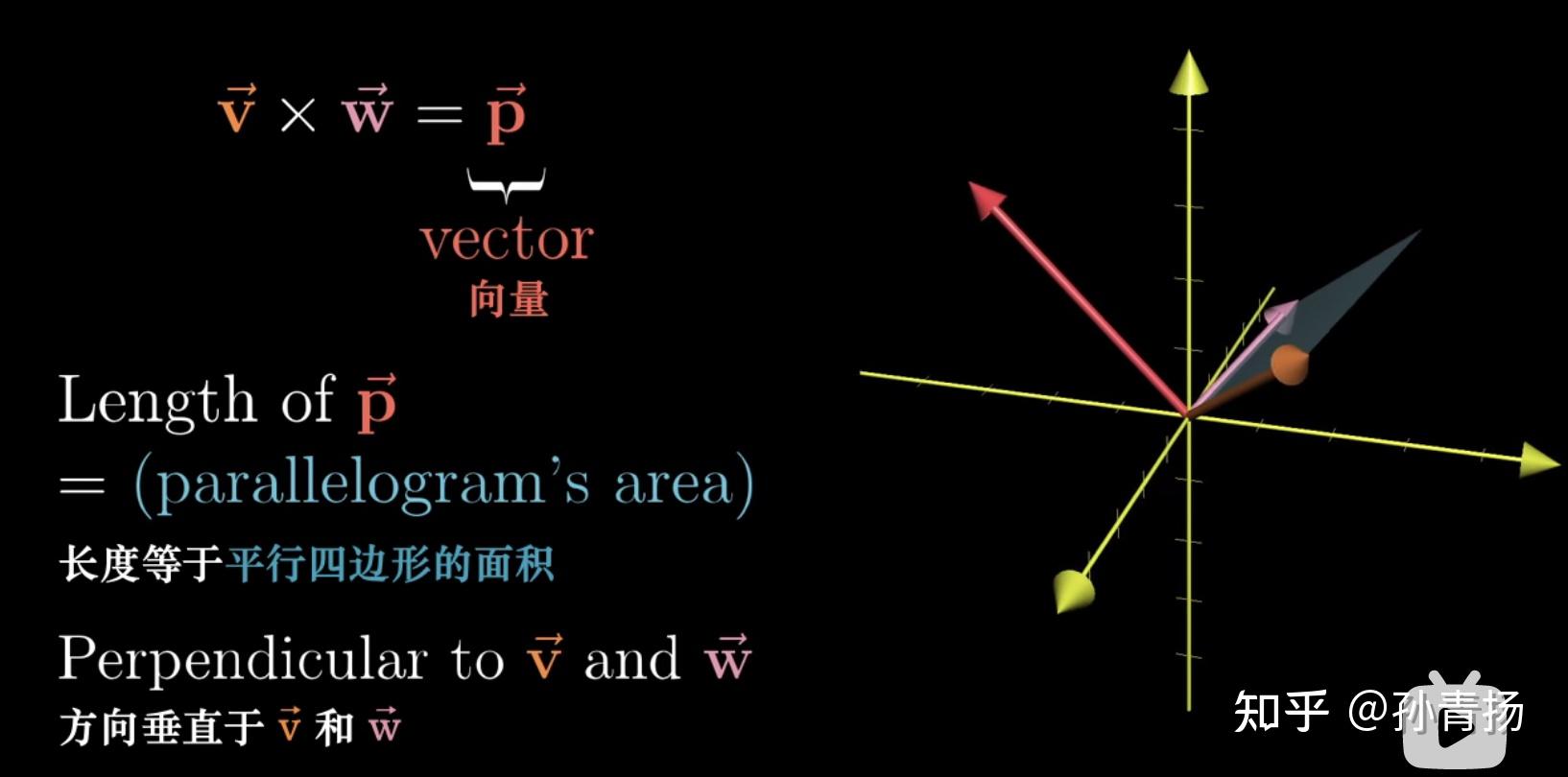
叉积是向量积，得出的结果是一个向量，这个向量是相当于“升了一维”，假如向量$\vec{a}$和向量$\vec{b}$都是二维的向量，那么它们的叉积就是垂直于这个二维平面的，

如图，叉积向量的方向垂直于原来那两个向量。

本文的主要内容，就是这个公式的推导。

公式推导

如图，两个向量分别指向$(x_1,y_1)$和$(x_2,y_2)$

这两个向量进行叉积运算后的结果$\vec{V}$，它的模长$|\vec{V}|$的几何意义是两个向量产生的平行四边形的面积（注意，这个面积是有向的，可能为负数）

我们用初中数学的方法，把四边形切割，然后依次计算。

$$\begin{gathered} S_1=\frac{1}{2}{y}_1(x_2+x_1+x_2) \\ {S}_2=\frac{1}{2}{x}_2{y}_2 \\ {S}_3=\frac{1}{2}{x}_1{y}_1 \\ {S}_4=\frac{1}{2}{x}_2(y_1+y_1+y_2) \\ {S}_{\text{总}}=S_1+S_2+S_3+S_4 \\ =\frac{2x_2{y}_1+x_1{y}_1+x_2{y}_2+x_1{y}_1+2x_2{y}_1+x_2{y}_2}{2} \\ =2x_2{y}_1+x_1{y}_1+x_2{y}_2 \\ {S}_{\text{平行四边形}}=(x_1+x_2)(y_1+y_2)-S_{\text{总}} \\ =x_1{y}_1+x_1{y}_2+x_2{y}_1+x_2{y}_2-2x_2{y}_1-x_1{y}_1-x_2{y}_2 \\ =x_1{y}_2-x_2{y}_1 \end{gathered}$$