高等数学：微分

大家好，欢迎来到IT知识分享网。

本文主要参考视频：

【建议收藏】同济七版《高等数学》精讲视频 | 期末考试 | 考研零基础 | 高数小白_哔哩哔哩_bilibili

3.3.1.1 微分的定义_哔哩哔哩_bilibili

3.3.5.1 导数与微分区别_哔哩哔哩_bilibili

仅供本人学习使用。

什么是微分

相对于导数来说，微分其实不是很好理解。一开始我就理解错了，把dy就理解成了△y，但二者并非完全等价的关系。

那到底什么是微分呢？

先看一个小的引例：

试问，这里如果用2×0*△x来近似替代△A，是否可行呢？

为了解决这个疑惑，我们就要先学习微分这个概念。

由微分的定义可知，因为A*△x，即dy相对于△y来说少了个高阶无穷小，所以二者并非完全等价。

事实上，微分dy就是函数的增量△y的近似表示，当△x无限趋近于0时，二者才越来越接近，这就是“以直代曲”的极限逼近思想，也是微分的核心思想。

以下有几点说明：

微分的几何意义

这里能很直观地看到，微分其实是“以直代曲”所产生的切线的函数值相对于△x的增量。

而切线是怎么来的呢？是求导数得来的。

所以，微分和导数是不是有什么关联呢？

事实上，对于一元函数来说，可微和可导是完全等价的。

可微的充要条件如下：

结论如下：

所以，才有导数的另一个叫法就是微商。

注意：这里的前提y=x才得出dx=△x，总感觉不完善。

参考：微分 dx, △x – 知乎

我们知道直线的斜率是y=kx，类似的，微分dy=导数*dx

因此，求微分，其实本质就是求导数，然后乘以自变量的微分dx，从而得到函数值的增量的近似表示。

举个求微分的简单例子

从例子中可以看出，微分dy其实是一个关于△x的线性函数。

微分和导数的区别

上面说可微和可导是等价的，那么这二者真的就是同一个东西吗？

还是有区别的。

微分的运算法则

基本初等函数的微分公式

其实就是求导函数，然后再乘以dx

四则运算

复合函数的微分

先外层整个求导，然后内层求导，相乘后再乘以dx

举个简单的例子

再举个例子

 

微分中值定理

微分中值定理并不是指某一个定理，而是一系列中值定理的总称，说是微分中值定理，其实和上面说的微分dy没有太大关系。

这些中值定理是研究函数的有力工具，其中最重要的内容是拉格朗日定理，可以说其他中值定理都是拉格朗日中值定理的特殊情况或推广。微分中值定理反映了导数的局部性与函数的整体性之间的关系，应用十分广泛。

之前在讲函数连续性的时候，讲过闭区间上连续函数的几个定理：

✔最大最小值定理

✔零点定理

✔介值定理  

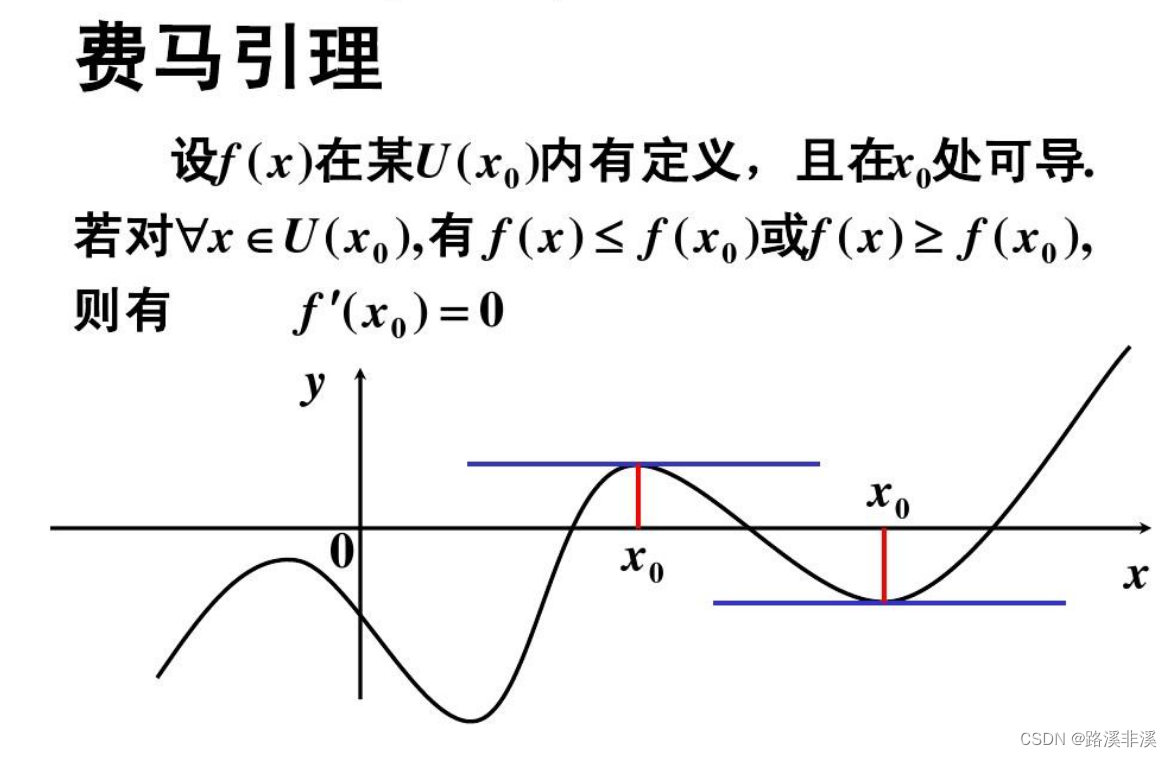
费马引理

说明x0这点要么是最凸点或者最凹点，也就是说要么是最大值要么是最小值。

费马引理要说的是：如果某个极限区域内的极值存在，那么极值处的导数为0

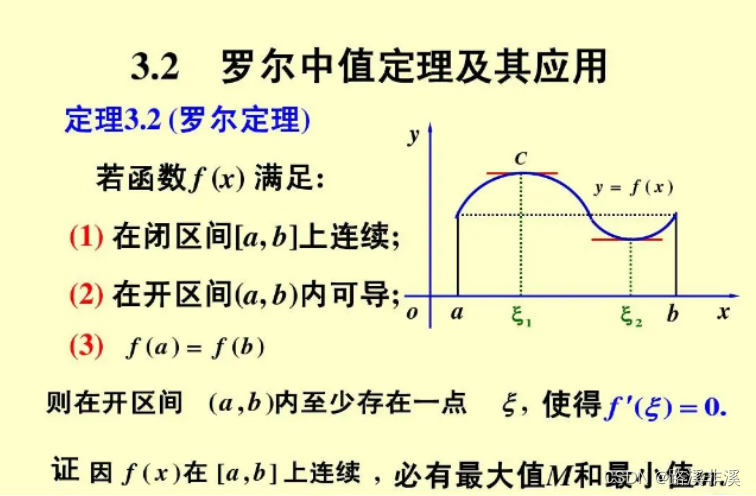
罗尔定理

这个很好理解，区间端点处函数值相等，则中间要么变大再变小，要么变小再变大，要么一直都没变，不管怎么样，都会有一个点的切线平行于x轴。

这也就是罗尔定理的几何意义

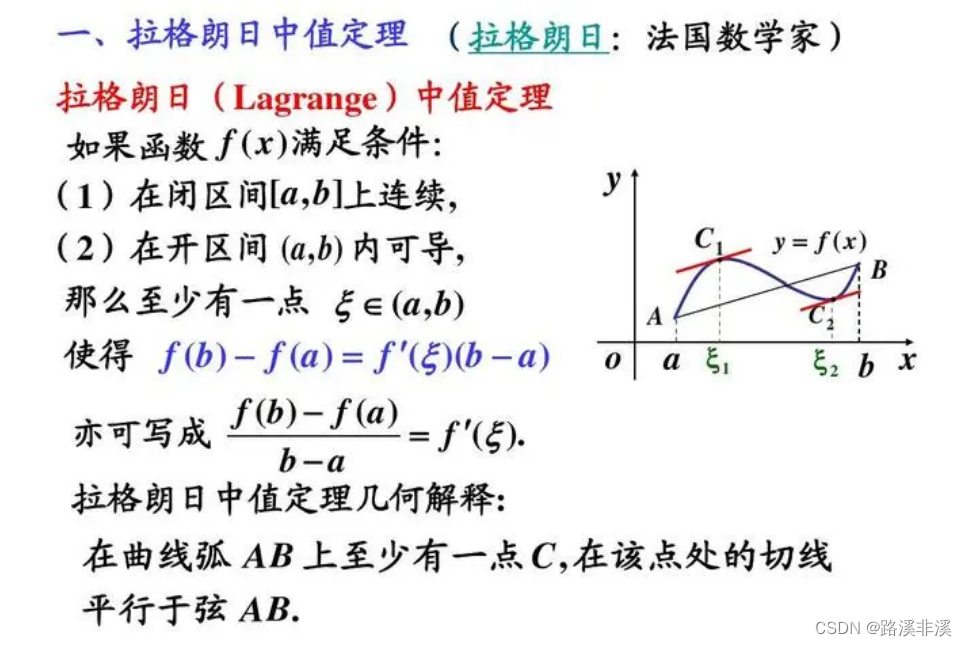
拉格朗日中值定理

罗尔定理其实是拉格朗日中值定理的一种特殊情况。

推广

几何意义

注意，这里是平行于弦AB，不是平行于x轴，别搞懵了。

柯西中值定理

洛必达法则我放到导数章节了。 高等数学：导数-CSDN博客

泰勒公式 

泰勒公式是一种用于近似表达函数在某一点附近的值的数学公式。它利用函数在该点的各阶导数值作为系数，构建一个多项式来近似表达这个函数。泰勒公式的提出归功于18世纪的英国数学家布鲁克·泰勒。这个公式广泛应用于函数微分学的相关领域，特别是在研究和分析复杂函数的性质时。

泰勒公式的正确性是基于拉格朗日的切线定理，而其近似性则是通过泰勒级数的展开得到的。泰勒级数是对原始函数进行无限次多项式展开的结果，其中每一项都是函数在不同阶导数处的线性组合。泰勒多项式是原函数的近似，随着多项式项数的增加，它会变得更加精确地接近原函数。 泰勒公式的发展历程涉及到了多位数学家的贡献，其中包括科林·麦克劳林和奥古斯丁-路易斯·柯西等人。他们的工作进一步扩展了泰勒公式的应用范围和使用频率，使其成为了分析和研究许多数学问题的有力工具。

1

2

3

可以看到，麦克劳林公式是对泰勒公式的简化，但也属于泰勒公式，我们一般都称之为泰勒展开。

下面是常用的泰勒展开式：

这些式子是已经计算并展开了，记住就行。

泰勒展开描述了任何函数都可以展开成多项式的形式，展开的项越多，越能接近真实值。

如何用泰勒公式求极限？

当我们直接求极限不好求的时候，就可以将式子进行泰勒展开，然后再求极限，极限情况下，高阶无穷小，即余项就会等于0。

注意：x^n的高阶无穷小就是说比n次幂还高次幂的余项。