大家好,欢迎来到IT知识分享网。
一个高中就学过的问题:现有一个m * n的网格,从最左上角出发,每次只能向右或者向下移动一格,问有多少种不同的方法可以到达最右下角的格子?
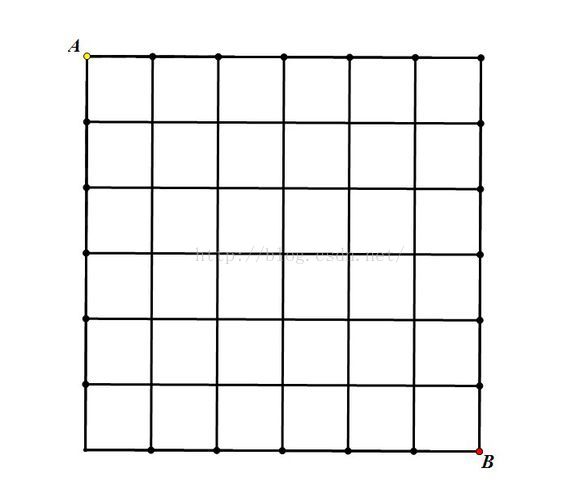
可以用高中学过的排列组合来解,见下图一个6*6的格子,从A走到B:
要从A到B,必须向左走6步,向下也走6步,一共12步,我们可以从向下走入手,向下走的方法即从12步里选出6步向下,一共有C(12,6)种,因此从A到B的路线共有组合数C(12,6)种。
对于m*n的格子,一样的,就是从m+n步中选出m步向下或n步向右,因此为C(m+n,m)=C(m+n,n)种。
简单编程即可得到。
另一种方法,采用动
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/143832.html