大家好，欢迎来到IT知识分享网。
目录
定义：
循环码：
定义 ： 记
为线性分组码的码字集，如果对任意的
， 循环左移或循环右移任意位后得到的码字
，仍有
，则称该线性分组码为循环码。
码多项式：
码字
与多项式可建立如下的对应关系。
码多项式系数的加乘运算规则：
加运算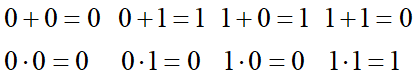
乘运算
整数域中的同余类：
在整数除法中，取定整数除数n，将所有整数m按除以所得的余数进行分类，余数相同的整数归为一类，称为关于n的同余类
Q与p均为整数。关于n的同余类记为
多项式域中的同余类：
同理可定义关于
多项式的同余类
记为 
示例：
多项式
是关于多项式
的同余类。
因为
即两者的余式相同。
循环码的代数结构(有关循环码的主要定理)：
1，若
是长度为n的循环码中的一个码多项式，i为不等于零的整数，则
按模
运算的余式必为循环码中的另一码多项式。
2，在循环码
中，幂次数为
，且其常数项不等于“0”的码字多项式
有一个且只有一个。因为多项式
的幂均小于n，由上述两个定理，可知这些多项式均为码多项式。
可知矩阵g中的每一行均为一个码字。因为矩阵g的秩为k，可知相应的k个码字互不相关，因此可以构成相应的码字空间的一组基。因此可定义相应的码多项式生成矩阵：
相应地可定义码的生成多项式 
给定信息码组
，由码多项式生成矩阵，可得相应的码多项式为
3，在循环码中，所有的码多项式
都可以被生成多项式
整除。
因为
所以定理的结论成立。
4，次数不大于
次的任何多项式与生成多项式的乘积都为码多项式。
5，循环码的生成多项式
是多项式
的一个因式。
生成多项式的充要条件：
（1）
是一个
次的多项式；
（2）
的常数项不等于0；
（3）
是
的一个因式。
定义式
为循环码的一致校验多项式。
因为码多项式可以表示为
因此有
由此，可利用一致校验多项式对接收的码字进行差错校验。
系统码结构的循环码：
输入信息位与对应的多项式
由
根据推论，且该多项式对应的码字具有系统码结构，因此该码为系统码结构的循环码。
系统码结构的循环码的生成矩阵和监督矩阵：
已知系统码结构的线性分组码生成矩阵为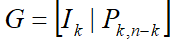
系统码结构的循环码码多项式的一般形式
根据生成矩阵每一行对应相应一个特殊码字的特点
由此可导出系统码结构循环码的生成矩阵。
循环码的编码器与译码器电路实现：
在各种专用和通用的数字信号处理器和计算机在通信设备中获得广泛应用之前，采用带反馈的移位寄存器结构的电路是实现循环码编译码器的主要途径。
循环码编译码电路主要由除法器组成。
除法电路：
已知除多项式
相应的除法电路为
一般地，若被除式
的最高次幂为
，需要
次移位完成除法运算；
商在除法器运算过程中移位输出；运算结束后，余式保留在寄存器内。
完成一次除法运算需要n个时钟信号，此后将余式从移位寄存器中移出另外需要r个时钟，共需要 n + r 个时钟
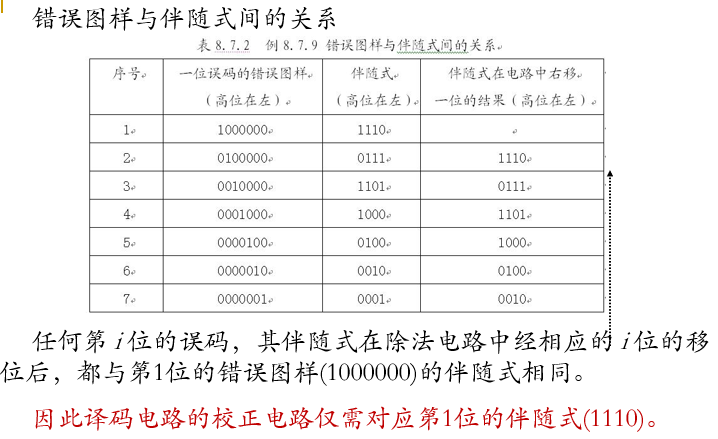
除法电路状态变化如表所示：
先行进位除法电路：
一般地，最高次幂为r的除法电路共有r个寄存单元，前述的除法电路在前面的r个时钟实际上是在做除法运算前的准备。
普通的除法电路运算的因准备阶段的用时，时延较大。
先行进位除法电路结构
直接将除式送到最高位，节省准备阶段的移位时间，完成一次除法运算并将余式移出只需n个时钟，效率较高。
系统码结构的循环码编码器：
除式即为生成多项式
除式的最高次幂：r＝n－k
编码过程：
循环码是线性分组码的一种，一般的线性分组码的译码方法均可用于循环码的译码。
利用循环码的特点，译码电路的实现通常可更为简单。
循环码译码原理：
译码的基本方法：
(1) 根据接收码字计算伴随式
(2) 由伴随式确定错误图样
(3) 进行纠错操作
注意：在码的纠错纠错能力范围才能实现真正的误码纠正。
循环码的译码特点：
汉明循环码：
汉明循环码是汉明码的一个子类。有关汉明循环码有如下的定理：
因为有限域中的本原多项式可以通过计算机遍历搜索的方法得到，因此定理8.7.8提供了一种构造具有汉明循环码的一般方法。
已知的可构造汉明循环码的参数表：
免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/146328.html
