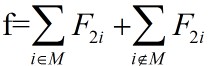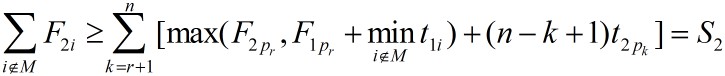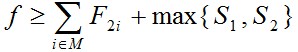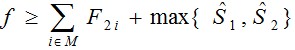大家好,欢迎来到IT知识分享网。
给定n个作业的集合{J1,J2,…,Jn}。每个作业必须先由机器1处理,然后由机器2处理。作业Ji需要机器j的处理时间为tji。对于一个确定的作业调度,设Fji是作业i在机器j上完成处理的时间。所有作业在机器2上完成处理的时间和称为该作业调度的完成时间和。
批处理作业调度问题要求对于给定的n个作业,制定最佳作业调度方案,使其完成时间和达到最小。
例:设n=3,考虑以下实例:
这3个作业的6种可能的调度方案是1,2,3;1,3,2;2,1,3;2,3,1;3,1,2;3,2,1;它们所相应的完成时间和分别是19,18,20,21,19,19。易见,最佳调度方案是1,3,2,其完成时间和为18。
限界函数
批处理作业调度问题要从n个作业的所有排列中找出具有最小完成时间和的作业调度,所以如图,批处理作业调度问题的解空间是一颗排列树。
在作业调度问相应的排列空间树中,每一个节点E都对应于一个已安排的作业集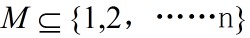
设|M|=r,且L是以节点E为根的子树中的叶节点,相应的作业调度为{pk,k=1,2,……n},其中pk是第k个安排的作业。如果从节点E到叶节点L的路上,每一个作业pk在机器1上完成处理后都能立即在机器2上开始处理,即从pr+1开始,机器1没有空闲时间,则对于该叶节点L有:
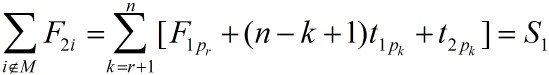
如果不能做到上面这一点,则s1只会增加,从而有: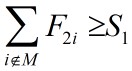
类似地,如果从节点E开始到节点L的路上,从作业pr+1开始,机器2没有空闲时间,则:
同理可知,s2是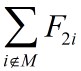
注意到如果选择Pk,使t1pk在k>=r+1时依非减序排列,S1则取得极小值。同理如果选择Pk使t2pk依非减序排列,则S2取得极小值。
这可以作为优先队列式分支限界法中的限界函数。
算法描述
算法中用最小堆表示活节点优先队列。最小堆中元素类型是MinHeapNode。每一个MinHeapNode类型的节点包含域x,用来表示节点所相应的作业调度。s表示该作业已安排的作业时x[1:s]。f1表示当前已安排的作业在机器1上的最后完成时间;f2表示当前已安排作业在机器2上的完成时间;sf2表示当前已安排的作业在机器2上的完成时间和;bb表示当前完成时间和下界。二维数组M表示所给的n个作业在机器1和机器2所需的处理时间。在类Flowshop中用二维数组b存储排好序的作业处理时间。数组a表示数组M和b的对应关系。算法Sort实现对各作业在机器1和2上所需时间排序。函数Bound用于计算完成时间和下界。
函数BBFlow中while循环完成对排列树内部结点的有序扩展。在while循环体内算法依次从活结点优先队列中取出具有最小bb值(完成时间和下界)的结点作为当前扩展结点,并加以扩展。 算法将当前扩展节点E分两种情形处理:
1)首先考虑E.s=n的情形,当前扩展结点E是排列树中的叶结点。E.sf2是相应于该叶结点的完成时间和。当E.sf2 < bestc时更新当前最优值bestc和相应的当前最优解bestx。
2)当E.s<n时,算法依次产生当前扩展结点E的所有儿子结点。对于当前扩展结点的每一个儿子结点node,计算出其相应的完成时间和的下界bb。当bb < bestc时,将该儿子结点插入到活结点优先队列中。而当bb bestc时,可将结点node舍去。
算法具体实现如下:
1、MinHeap2.h
- #include <iostream>
- template<class Type>
- class Graph;
- template<class T>
- class MinHeap
- {
- template<class Type>
- friend class Graph;
- public:
- MinHeap(int maxheapsize = 10);
- ~MinHeap(){
delete []heap;} - int Size() const{
return currentsize;} - T Max(){
if(currentsize) return heap[1];} - MinHeap<T>& Insert(const T& x);
- MinHeap<T>& DeleteMin(T &x);
- void Initialize(T x[], int size, int ArraySize);
- void Deactivate();
- void output(T a[],int n);
- private:
- int currentsize, maxsize;
- T *heap;
- };
- template <class T>
- void MinHeap<T>::output(T a[],int n)
- {
- for(int i = 1; i <= n; i++)
- cout << a[i] << ” “;
- cout << endl;
- }
- template <class T>
- MinHeap<T>::MinHeap(int maxheapsize)
- {
- maxsize = maxheapsize;
- heap = new T[maxsize + 1];
- currentsize = 0;
- }
- template<class T>
- MinHeap<T>& MinHeap<T>::Insert(const T& x)
- {
- if(currentsize == maxsize)
- {
- return *this;
- }
- int i = ++currentsize;
- while(i != 1 && x < heap[i/2])
- {
- heap[i] = heap[i/2];
- i /= 2;
- }
- heap[i] = x;
- return *this;
- }
- template<class T>
- MinHeap<T>& MinHeap<T>::DeleteMin(T& x)
- {
- if(currentsize == 0)
- {
- cout<<“Empty heap!”<<endl;
- return *this;
- }
- x = heap[1];
- T y = heap[currentsize–];
- int i = 1, ci = 2;
- while(ci <= currentsize)
- {
- if(ci < currentsize && heap[ci] > heap[ci + 1])
- {
- ci++;
- }
- if(y <= heap[ci])
- {
- break;
- }
- heap[i] = heap[ci];
- i = ci;
- ci *= 2;
- }
- heap[i] = y;
- return *this;
- }
- template<class T>
- void MinHeap<T>::Initialize(T x[], int size, int ArraySize)
- {
- delete []heap;
- heap = x;
- currentsize = size;
- maxsize = ArraySize;
- for(int i = currentsize / 2; i >= 1; i–)
- {
- T y = heap[i];
- int c = 2 * i;
- while(c <= currentsize)
- {
- if(c < currentsize && heap[c] > heap[c + 1])
- c++;
- if(y <= heap[c])
- break;
- heap[c / 2] = heap[c];
- c *= 2;
- }
- heap[c / 2] = y;
- }
- }
- template<class T>
- void MinHeap<T>::Deactivate()
- {
- heap = 0;
- }
#include <iostream> template<class Type> class Graph; template<class T> class MinHeap { template<class Type> friend class Graph; public: MinHeap(int maxheapsize = 10); ~MinHeap(){delete []heap;} int Size() const{return currentsize;} T Max(){if(currentsize) return heap[1];} MinHeap<T>& Insert(const T& x); MinHeap<T>& DeleteMin(T &x); void Initialize(T x[], int size, int ArraySize); void Deactivate(); void output(T a[],int n); private: int currentsize, maxsize; T *heap; }; template <class T> void MinHeap<T>::output(T a[],int n) { for(int i = 1; i <= n; i++) cout << a[i] << " "; cout << endl; } template <class T> MinHeap<T>::MinHeap(int maxheapsize) { maxsize = maxheapsize; heap = new T[maxsize + 1]; currentsize = 0; } template<class T> MinHeap<T>& MinHeap<T>::Insert(const T& x) { if(currentsize == maxsize) { return *this; } int i = ++currentsize; while(i != 1 && x < heap[i/2]) { heap[i] = heap[i/2]; i /= 2; } heap[i] = x; return *this; } template<class T> MinHeap<T>& MinHeap<T>::DeleteMin(T& x) { if(currentsize == 0) { cout<<"Empty heap!"<<endl; return *this; } x = heap[1]; T y = heap[currentsize--]; int i = 1, ci = 2; while(ci <= currentsize) { if(ci < currentsize && heap[ci] > heap[ci + 1]) { ci++; } if(y <= heap[ci]) { break; } heap[i] = heap[ci]; i = ci; ci *= 2; } heap[i] = y; return *this; } template<class T> void MinHeap<T>::Initialize(T x[], int size, int ArraySize) { delete []heap; heap = x; currentsize = size; maxsize = ArraySize; for(int i = currentsize / 2; i >= 1; i--) { T y = heap[i]; int c = 2 * i; while(c <= currentsize) { if(c < currentsize && heap[c] > heap[c + 1]) c++; if(y <= heap[c]) break; heap[c / 2] = heap[c]; c *= 2; } heap[c / 2] = y; } } template<class T> void MinHeap<T>::Deactivate() { heap = 0; } 2、6d9.cpp
- //批作业调度问题 优先队列分支限界法求解
- #include “stdafx.h”
- #include “MinHeap2.h”
- #include <iostream>
- using namespace std;
- class Flowshop;
- class MinHeapNode
- {
- friend Flowshop;
- public:
- operator int() const
- {
- return bb;
- }
- private:
- void Init(int);
- void NewNode(MinHeapNode,int,int,int,int);
- int s, //已安排作业数
- f1, //机器1上最后完成时间
- f2, //机器2上最后完成时间
- sf2, //当前机器2上完成时间和
- bb, //当前完成时间和下界
- *x; //当前作业调度
- };
- class Flowshop
- {
- friend int main(void);
- public:
- int BBFlow(void);
- private:
- int Bound(MinHeapNode E,int &f1,int &f2,bool y);
- void Sort(void);
- int n, //作业数
- M, //各作业所需的处理时间数组
- b, //各作业所需的处理时间排序数组
- a, //数组M和b的对应关系数组
- *bestx, //最优解
- bestc; //最小完成时间和
- bool y; //工作数组
- };
- template <class Type>
- inline void Swap(Type &a, Type &b);
- int main()
- {
- int n=3,bf;
- int M1[3][2]={
{2,1},{3,1},{2,3}}; - int M = new int*[n];
- int b = new int*[n];
- int a = new int*[n];
- bool y = new bool*[n];
- int *bestx = new int[n];
- for(int i=0;i<=n;i++)
- {
- M[i] = new int[2];
- b[i] = new int[2];
- a[i] = new int[2];
- y[i] = new bool[2];
- }
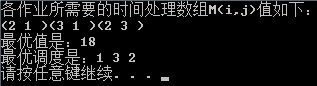
- cout<<“各作业所需要的时间处理数组M(i,j)值如下:”<<endl;
- for(int i=0;i<n;i++)
- {
- for(int j=0;j<2;j++)
- {
- M[i][j]=M1[i][j];
- }
- }
- for(int i=0;i<n;i++)
- {
- cout<<“(“;
- for(int j=0;j<2;j++)
- cout<<M[i][j]<<” “;
- cout<<“)”;
- }
- cout<<endl;
- Flowshop flow;
- flow.n = n;
- flow.M = M;
- flow.b = b;
- flow.a = a;
- flow.y = y;
- flow.bestx = bestx;
- flow.bestc = 1000;//给初值
- flow.BBFlow();
- cout<<“最优值是:”<<flow.bestc<<endl;
- cout<<“最优调度是:”;
- for(int i=0;i<n;i++)
- {
- cout<<(flow.bestx[i]+1)<<” “;
- }
- cout<<endl;
- for(int i=0;i<n;i++)
- {
- delete[] M[i];
- delete[] b[i];
- delete[] a[i];
- delete[] y[i];
- }
- return 0;
- }
- //最小堆节点初始化
- void MinHeapNode::Init(int n)
- {
- x = new int[n];
- for(int i=0; i<n; i++)
- {
- x[i] = i;
- }
- s = 0;
- f1 = 0;
- f2 = 0;
- sf2 = 0;
- bb = 0;
- }
- //最小堆新节点
- void MinHeapNode::NewNode(MinHeapNode E,int Ef1,int Ef2,int Ebb,int n)
- {
- x = new int[n];
- for(int i=0; i<n; i++)
- {
- x[i] = E.x[i];
- }
- f1 = Ef1;
- f2 = Ef2;
- sf2 = E.sf2 + f2;
- bb = Ebb;
- s = E.s + 1;
- }
- //对各作业在机器1和2上所需时间排序
- void Flowshop::Sort(void)
- {
- int *c = new int[n];
- for(int j=0; j<2; j++)
- {
- for(int i=0; i<n; i++)
- {
- b[i][j] = M[i][j];
- c[i] = i;
- }
- for(int i=0; i<n-1; i++)
- {
- for(int k=n-1; k>i; k–)
- {
- if(b[k][j]<b[k-1][j])
- {
- Swap(b[k][j],b[k-1][j]);
- Swap(c[k],c[k-1]);
- }
- }
- }
- for(int i=0; i<n; i++)
- {
- a[c[i]][j] = i;
- }
- }
- delete []c;
- }
- //计算完成时间和下界
- int Flowshop::Bound(MinHeapNode E,int &f1,int &f2,bool y)
- {
- for(int k=0; k<n; k++)
- {
- for(int j=0; j<2; j++)
- {
- y[k][j] = false;
- }
- }
- for(int k=0; k<=E.s; k++)
- {
- for(int j=0; j<2; j++)
- {
- y[a[E.x[k]][j]][j] = true;
- }
- }
- f1 = E.f1 + M[E.x[E.s]][0];
- f2 = ((f1>E.f2)?f1:E.f2)+M[E.x[E.s]][1];
- int sf2 = E.sf2 + f2;
- int s1 = 0,s2 = 0,k1 = n-E.s,k2 = n-E.s,f3 = f2;
- //计算s1的值
- for(int j=0; j<n; j++)
- {
- if(!y[j][0])
- {
- k1–;
- if(k1 == n-E.s-1)
- {
- f3 = (f2>f1+b[j][0])?f2:f1+b[j][0];
- }
- s1 += f1+k1*b[j][0];
- }
- }
- //计算s2的值
- for(int j=0; j<n; j++)
- {
- if(!y[j][1])
- {
- k2–;
- s1 += b[j][1];
- s2 += f3 + k2*b[j][1];
- }
- }
- //返回完成时间和下界
- return sf2 +((s1>s2)?s1:s2);
- }
- //解批处理作业调度问题的优先队列式分支限界法
- int Flowshop::BBFlow(void)
- {
- Sort();//对各作业在机器1和2上所需时间排序
- MinHeap<MinHeapNode> H(1000);
- MinHeapNode E;
- //初始化
- E.Init(n);
- //搜索排列空间树
- while(E.s<=n)
- {
- //叶节点
- if(E.s == n)
- {
- if(E.sf2<bestc)
- {
- bestc = E.sf2;
- for(int i=0; i<n; i++)
- {
- bestx[i] = E.x[i];
- }
- }
- delete []E.x;
- }
- else//产生当前扩展节点的儿子节点
- {
- for(int i=E.s; i<n; i++)
- {
- Swap(E.x[E.s],E.x[i]);
- int f1,f2;
- int bb = Bound(E,f1,f2,y);
- if(bb<bestc)
- {
- //子树可能含有最优解
- //节点插入最小堆
- MinHeapNode N;
- N.NewNode(E,f1,f2,bb,n);
- H.Insert(N);
- }
- Swap(E.x[E.s],E.x[i]);
- }
- delete []E.x;//完成节点扩展
- }
- if(H.Size() == 0)
- {
- break;
- }
- H.DeleteMin(E);//取下一扩展节点
- }
- return bestc;
- }
- template <class Type>
- inline void Swap(Type &a, Type &b)
- {
- Type temp=a;
- a=b;
- b=temp;
- }
//批作业调度问题 优先队列分支限界法求解 #include "stdafx.h" #include "MinHeap2.h" #include <iostream> using namespace std; class Flowshop; class MinHeapNode { friend Flowshop; public: operator int() const { return bb; } private: void Init(int); void NewNode(MinHeapNode,int,int,int,int); int s, //已安排作业数 f1, //机器1上最后完成时间 f2, //机器2上最后完成时间 sf2, //当前机器2上完成时间和 bb, //当前完成时间和下界 *x; //当前作业调度 }; class Flowshop { friend int main(void); public: int BBFlow(void); private: int Bound(MinHeapNode E,int &f1,int &f2,bool y); void Sort(void); int n, //作业数 M, //各作业所需的处理时间数组 b, //各作业所需的处理时间排序数组 a, //数组M和b的对应关系数组 *bestx, //最优解 bestc; //最小完成时间和 bool y; //工作数组 }; template <class Type> inline void Swap(Type &a, Type &b); int main() { int n=3,bf; int M1[3][2]={
{2,1},{3,1},{2,3}}; int M = new int*[n]; int b = new int*[n]; int a = new int*[n]; bool y = new bool*[n]; int *bestx = new int[n]; for(int i=0;i<=n;i++) { M[i] = new int[2]; b[i] = new int[2]; a[i] = new int[2]; y[i] = new bool[2]; } cout<<"各作业所需要的时间处理数组M(i,j)值如下:"<<endl; for(int i=0;i<n;i++) { for(int j=0;j<2;j++) { M[i][j]=M1[i][j]; } } for(int i=0;i<n;i++) { cout<<"("; for(int j=0;j<2;j++) cout<<M[i][j]<<" "; cout<<")"; } cout<<endl; Flowshop flow; flow.n = n; flow.M = M; flow.b = b; flow.a = a; flow.y = y; flow.bestx = bestx; flow.bestc = 1000;//给初值 flow.BBFlow(); cout<<"最优值是:"<<flow.bestc<<endl; cout<<"最优调度是:"; for(int i=0;i<n;i++) { cout<<(flow.bestx[i]+1)<<" "; } cout<<endl; for(int i=0;i<n;i++) { delete[] M[i]; delete[] b[i]; delete[] a[i]; delete[] y[i]; } return 0; } //最小堆节点初始化 void MinHeapNode::Init(int n) { x = new int[n]; for(int i=0; i<n; i++) { x[i] = i; } s = 0; f1 = 0; f2 = 0; sf2 = 0; bb = 0; } //最小堆新节点 void MinHeapNode::NewNode(MinHeapNode E,int Ef1,int Ef2,int Ebb,int n) { x = new int[n]; for(int i=0; i<n; i++) { x[i] = E.x[i]; } f1 = Ef1; f2 = Ef2; sf2 = E.sf2 + f2; bb = Ebb; s = E.s + 1; } //对各作业在机器1和2上所需时间排序 void Flowshop::Sort(void) { int *c = new int[n]; for(int j=0; j<2; j++) { for(int i=0; i<n; i++) { b[i][j] = M[i][j]; c[i] = i; } for(int i=0; i<n-1; i++) { for(int k=n-1; k>i; k--) { if(b[k][j]<b[k-1][j]) { Swap(b[k][j],b[k-1][j]); Swap(c[k],c[k-1]); } } } for(int i=0; i<n; i++) { a[c[i]][j] = i; } } delete []c; } //计算完成时间和下界 int Flowshop::Bound(MinHeapNode E,int &f1,int &f2,bool y) { for(int k=0; k<n; k++) { for(int j=0; j<2; j++) { y[k][j] = false; } } for(int k=0; k<=E.s; k++) { for(int j=0; j<2; j++) { y[a[E.x[k]][j]][j] = true; } } f1 = E.f1 + M[E.x[E.s]][0]; f2 = ((f1>E.f2)?f1:E.f2)+M[E.x[E.s]][1]; int sf2 = E.sf2 + f2; int s1 = 0,s2 = 0,k1 = n-E.s,k2 = n-E.s,f3 = f2; //计算s1的值 for(int j=0; j<n; j++) { if(!y[j][0]) { k1--; if(k1 == n-E.s-1) { f3 = (f2>f1+b[j][0])?f2:f1+b[j][0]; } s1 += f1+k1*b[j][0]; } } //计算s2的值 for(int j=0; j<n; j++) { if(!y[j][1]) { k2--; s1 += b[j][1]; s2 += f3 + k2*b[j][1]; } } //返回完成时间和下界 return sf2 +((s1>s2)?s1:s2); } //解批处理作业调度问题的优先队列式分支限界法 int Flowshop::BBFlow(void) { Sort();//对各作业在机器1和2上所需时间排序 MinHeap<MinHeapNode> H(1000); MinHeapNode E; //初始化 E.Init(n); //搜索排列空间树 while(E.s<=n) { //叶节点 if(E.s == n) { if(E.sf2<bestc) { bestc = E.sf2; for(int i=0; i<n; i++) { bestx[i] = E.x[i]; } } delete []E.x; } else//产生当前扩展节点的儿子节点 { for(int i=E.s; i<n; i++) { Swap(E.x[E.s],E.x[i]); int f1,f2; int bb = Bound(E,f1,f2,y); if(bb<bestc) { //子树可能含有最优解 //节点插入最小堆 MinHeapNode N; N.NewNode(E,f1,f2,bb,n); H.Insert(N); } Swap(E.x[E.s],E.x[i]); } delete []E.x;//完成节点扩展 } if(H.Size() == 0) { break; } H.DeleteMin(E);//取下一扩展节点 } return bestc; } template <class Type> inline void Swap(Type &a, Type &b) { Type temp=a; a=b; b=temp; }
程序运行结果如图:
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/147098.html