博弈论 详解

大家好，欢迎来到IT知识分享网。

一、博弈论简介

博弈论 ，是经济学的一个分支，主要研究具有竞争或对抗性质的对象，在一定规则下产生的各种行为。博弈论考虑游戏中的个体的预测行为和实际行为，并研究它们的优化策略。

通俗地讲，博弈论主要研究的是：在一个游戏中，进行游戏的多位玩家的策略。

对于算法竞赛中的博弈问题，一般具有以下特征：

• 博弈模型为两人轮流决策的非合作博弈。即两人轮流进行决策，并且两人都使用最优策略来获取胜利。
• 博弈是有限的。即无论两人怎样决策，都会在有限步后决出胜负。
• 公平博弈。即两人进行决策所遵循的规则相同。

二、基本概念

1.公平组合游戏

公平组合游戏的定义如下：

• 游戏有两个人参与，二者轮流做出决策，双方均知道游戏的完整信息；
• 任意一个游戏者在某一确定状态可以作出的决策集合只与当前的状态有关，而与游戏者无关；
• 游戏中的同一个状态不可能多次抵达，游戏以玩家无法行动为结束，且游戏一定会在有限步后以非平局结束。

大部分的棋类游戏都 不是 公平组合游戏，如国际象棋、中国象棋、围棋、五子棋等（因为双方都不能使用对方的棋子）。

公平游戏具有一个重要的性质：

如果一个游戏者能够讲状态A变为状态B，那么另外一个游戏者必然也能实现这样的操作。

2.博弈图和状态

1).博弈图

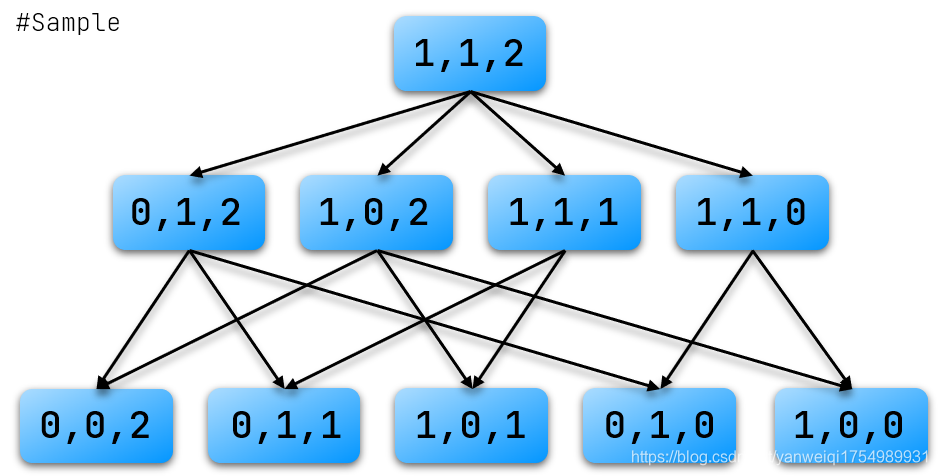
如果将每个状态视为一个节点，再从每个状态向它的后继状态连边，我们就可以得到一个博弈状态图。

如上图，我们假定存在博弈状态$(i,j,k)$，表示局面为$(i,j,k)$的状态，则我们可以根据状态的转移确定博弈图。

易知：博弈图必为DAG(有向无环图)。

2).状态

我们首先定义博弈中常用的两种状态：必胜态、必输态

1. 必胜态：先手必胜的状态
2. 必败态：先手必败的状态

同时我们对决策局面进行定义：

1. P局面：即为Previous-position，上次移动的人具有必胜策略的局面(先手必败)。
   • 任何无法移动的局面都是P局面
2. N局面：即为Next-position，当前移动的人具有必胜决策的场面(先手必胜)。
   • 可以移动到P局面的局面是N局面
   • 所有移动都导致移动到N局面的局面是P局面

有了状态的定义，对于博弈图中的状态点我们可以继续定义：

1. P点：必败点，某玩家位于此点，只要对方无失误，则必败
2. N点：必胜点，某玩家位于此点，只要自己无失误，则必胜

通过推理，我们可以得到以下三条定理：

• 定理 1：没有后继状态的状态是必败状态。(终止状态必为P局面)
• 定理 2：一个状态是必胜状态当且仅当存在至少一个必败状态为它的后继状态。(N局面的下一步中有一个是P局面)
• 定理 3：一个状态是必败状态当且仅当它的所有后继状态均为必胜状态。(P局面的下一步全部是N局面)

直接这样阐述有些难以理解，我们继续进行解释：

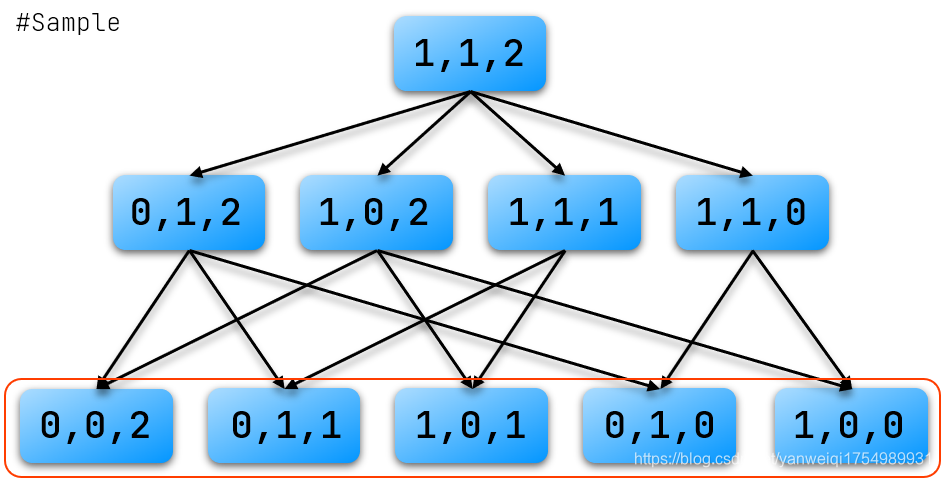
对于定理 1，如果游戏进行不下去了，那么这个玩家就输掉了游戏。对于这个状态是十分容易理解的–大多数游戏在此时已经无法继续进行(终结局面)，比如N堆石子任意取游戏，当N堆石子均为空时不会再出现任何的后继状态，此时的状态为必胜状态；

如图，红框内所示的状态点全部为“终结局面”

对于定理 2，如果该状态至少有一个后继状态为必败状态，那么玩家可以通过操作到该必败状态；此时对手的状态为必败状态——对手必定是失败的，而相反地，自己就获得了胜利。

换句话说，对于公平游戏而言，只有让对手走到必败状态，自己才能赢

对于定理 3，如果不存在一个后继状态为必败状态，那么无论如何，玩家只能操作到必胜状态；此时对手的状态为必胜状态——对手必定是胜利的，自己就输掉了游戏。

换句话说，你能到达必胜点且无法向必败点转移，那么你的对手也能到必胜点，这样你就输了。

如果博弈图是一个有向无环图，则通过这三个定理，我们可以在绘出博弈图的情况下用 $O(N+M)$ 的时间（其中 $N$ 为状态种数，$M$ 为边数）得出每个状态是必胜状态还是必败状态。

三、博弈模型

1.巴什博弈

巴什博弈属于基本的博弈问题，其典型特征为：

给定$n$堆物品，两个人轮流从这堆物品中取物品，规定每次最少取$1$个，最多取$m$个，最后取光者为胜。

当$n=m+1$时，由于一次最多只能取$m$个，所以无论先取者拿走多少个，后取者都能一次拿走剩余的物品，后取者取胜；

所以当一方面对的局势为$n=(m+1)\times r+s$（其中$r$为任意自然数，$s\le m$)，如果先取者要取走$s$个物品，如果后取者取走$x(x\le m)$个，那么后取者只要取走$m+1-k$个，结果剩下$(m-1)(r-1)$个，以后保持这样的取法，那么先取者肯定获胜，总之，要保持给对手留下$(m+1)$的倍数，就能最后获胜。

结论1：若$(m+1)|n$，则先手必败，否则先手必赢

一种常见的变形是“问题改为最后取光的人输”。那么此时的结论：

结论2：当$(n-1)\%(m+1)==0$时先手必输。

2.威佐夫博弈

威佐夫博弈问题具有的典型特征是：

有两堆各若干个物品，两个人轮流从某一堆或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

如何解决威佐夫博弈问题？

首先，我们定义$(a_i,b_i)(a_i\le b_i,i=1,2,...,n)$表示两堆物品的数量并称其为局势，如果甲面对$(0,0)$，那么甲已经输了，这种局势我们称为奇异局势。前几个奇异局势，前几个奇异局势为$(0,0)、(1,2)、(3,5)、(4,7)、(6,10)、(8,13)、(9,15)、(11,18)、(12,20)$。任意给定一个局势$(a,b)$，如下公式可以判断其是否为奇异局势：
$$a_k=\lfloor \frac{k\times (1+\sqrt{5})}{2}\rfloor ,b_k=a_k+k(k=0,1,2,...,n)$$
面对非奇异局势，先手必胜；面对奇异局势，先手必败。

满足上述公式的局势性质：

我们定义$(x,y)$为第$k$个奇异局势。

(1).任何自然数都包含在一个且仅有一个奇异局势中；

(2).$x$为前$1...k$个奇异局势中没有出现过的最小正整数，$y=x+k$；

(3).任何操作都会将奇异局势转化为非奇异局势；

(4).可以采取适当的方法将非奇异局势转化为奇异局势。

我们对以上的分析进行总结，可以得出威佐夫博弈的通解形式：

对于给定的两堆石子$(x,y)(x<y)$，排除操作失误的客观因素，那么先手必败，当且仅当：
$$(y-x)\times \frac{(\sqrt{5}+1)}{2}=x$$
我们可以很惊奇的发现：其中的$\frac{\sqrt{5}+1}{2}$就是我们所熟悉的黄金分割数！

实际上，黄金分割数在其他许多场景中都有很广泛的应用，利用好黄金分割相关的结论能够很轻松的解决许多问题。

在许多场景下，我们面对的并不是奇异局势，对于一部分问题，我们可以将非奇异局势转化为奇异局势。

假设面对的局势是$(a,b)$。（$b$大于等于$a$）
如果 $b=a$，则同时从两堆中取走 $a$ 个物体，就变为了奇异局势$(0，0)$；
如果 $a=a[k]，b>b[k]$ ,那么，取走$b-b[k]$个物体，即变为奇异局势；
如果 $a=a[k]，b<b[k]$ 则同时从两堆中拿走$a-a[b-a]$ 个物体(详见注释1)变为奇异局势$(a[b-a],a[b-a]+b-a)$；
如果$a>a[k]，b=a[k]+k$ 则从第一堆中拿走多余的数量$a-a[k]$ 即可；
如果$a<a[k]，b=a[k]+k$, 分两种情况：
第一种，$a=a[j](j<k)$从第二堆里面拿走 $b-b[j]$ 即可；
第二种，$a=b[j](j<k)$从第二堆里面拿走 $b-a[j]$ 即可（交换$a，b$）。

如何理解这个转换？

因为奇异局势的项数是有 $b[k]-a[k]$ 的差决定$(b=a[k]+k)$，每一个奇异局势的项数都是独一无二的。
也就是说，我们 只能将$(a,b)(a=a[k],b<b[k])$转化为$(a[b-a],b[b-a]）(a[b-a],a[b-a]+b-a)$。
因为他们的差是确定的始终都是 $b-a$，故可以转化为 第 $b-a$ 项。
由此我们可以 将$(a,b)(a=a[k],b<b[k])$ 转化为奇异局势 $(a[b-a],b[b-a])$也就是。
所以我们可以逆推得出，只要将 两边 同时减去$a-a[b-a]$即可。

注：以上局势变换引用自博客 Wythoff Game 非奇异局势变为奇异局势

3.斐波那契(Fibonacci)博弈

斐波那契博弈的典型特征是：

给定一堆个数为$n$的石子，两个玩家轮流取石子，满足：

1. 先手不能在第一次把所有的石子取光；
2. 第一次取完后的每次可以取得石子数介于1到对手刚取的石子数的2倍之间(包含1和对手刚取的石子数的2倍)；
3. 取走最后一个石子的人为玩家。

如何解决这一类博弈问题？

首先先给出结论：当$n$为斐波那契数的时候，先手必败，即存在先手的必败态当且仅当石头个数为Fibonacci数。

下面给出证明：

根据“Zeckendorf定理”（齐肯多夫定理）：任何正整数可以表示为若干个不连续的Fibonacci数之和。如$n=83=55+21+5+2$，我们看看这个分解有什么指导意义：假如先手取2颗，那么后手无法取5颗或更多，而5是一个Fibonacci数，那么一定是先手取走这5颗石子中的最后一颗，同理，接下去先手取走接下来的后21颗中的最后一颗，再取走后55颗中的最后一颗，那么先手赢。

反证：如果$n$是Fibonacci数，如$n=89$：记先手一开始所取的石子数为$y$

（1）若 $y\ge 34$ 颗（也就是$89$的向前两项），那么一定后手赢，因为$89-34=55=34+21<2\ast 34$。

（2）$y<34$ 时剩下的石子数$x$介于$55$到$89$之间，它一定不是一个Fibonacci数，把x分解成Fibonacci数：$x=55+f[i]+\dots +f[j]$，若，如果$f[j]<=2y$，那么对B就是面临x局面的先手，所以根据之前的分析，后手只要先取$f[j]$个即可，以后再按之前的分析就可保证必胜。

判断斐波那契数的方法可以采用通项公式法或遍历法。如果数据范围大会卡时间则考虑矩阵快速幂优化等。

4.Nim博弈

①.Nim游戏

Nim游戏是一个典型的博弈问题，建立在Nim游戏基础上的博弈一般都具有相同的框架特征。

$n$ 堆物品，每堆有 $a_i$ 个，两个玩家轮流取走任意一堆的任意个物品，但不能不取。取走最后一个物品的人获胜。

例如，如果现在有 $n=3$ 堆物品，而每堆分别有 $2,5,4$ 个，那么可以取走第 $1$ 堆中的 $2$ 个物品，局面就变成了 $0,5,4$；或者也可以取走第 $2$ 堆的 $4$ 个物品，局面就变成了 $2,1,4$。

如果现在的局面为 $0,0,5$，甲取走了第 $3$ 堆的 $5$ 个物品，也就是取走了最后一个物品，此时甲获胜。

②.Nim和

首先回顾“博弈图”。我们通过绘画博弈图，可以在 $O({\prod }_{i=1}^n{a}_i)$ 的时间里求出该局面是否先手必赢。

显然，这样的推导方式时间复杂度是非常高的，我们需要换一种思路进行推导。

定义 Nim 和 $=a_1\oplus a_2\oplus \dots \oplus a_n$。

那么当且仅当 Nim 和为 $0$ 时，该状态为必败状态；否则该状态为必胜状态。

为了证明该定理，只需要证明下面三个定理：

• 定理 1：没有后继状态的状态是必败状态。
• 定理 2：对于 $a_1\oplus a_2\oplus \dots \oplus a_n\ne 0$ 的局面，一定存在某种移动使得 $a_1\oplus a_2\oplus \dots \oplus a_n=0$。
• 定理 3：对于 $a_1\oplus a_2\oplus \dots \oplus a_n=0$ 的局面，一定不存在某种移动使得 $a_1\oplus a_2\oplus \dots \oplus a_n=0$。

对于定理 1，没有后继状态的状态只有一个，即全 $0$ 局面。此时 $a_1\oplus a_2\oplus \dots \oplus a_n=0$。

对于定理 2，不妨假设 $a_1\oplus a_2\oplus \dots a_n=k\ne 0$。如果我们要将 $a_i$ 改为 $a_i^{\prime }$，则 $a_i^{\prime }=a_i\oplus k$。

根据异或定义，一定有奇数个 $a_i$ 在 $k$ 在二进制下的最高位为 $1$。满足这个条件的 $a_i$ 一定也满足 $a_i>a_i\oplus k$，因而这也是个合法的移动。

对于定理 3，如果我们要将 $a_i$ 改为 $a_i^{\prime }$，则根据异或运算律可以得出 $a_i=a_i^{\prime }$，因而这不是个合法的移动。

四、公平组合博弈(ICG)与有向图游戏

1.公平组合博弈-定义

1. 两人参与
2. 游戏局面的状态集合是有限的
3. 对于同一个局面，两个游戏者可操控的集合完全相同
4. 游戏者轮流进行游戏
5. 当无法进行任何操作时游戏结束，此时不能进行操作的一方为输方
6. 无论游戏如何进行，总可以在有限的步数之内结束游戏

实际上，所有的公平组合博弈(ICG)都可以被转换为有向图游戏。

2.ICG模型

给定一个有向无环图和一个起始顶点上的一枚棋子，两名选手轮流交替移动棋子(沿着有向边移动)，无法移动者判定为输家。

我们一般将这种游戏框架模型统一归属为公平组合游戏(ICG).

我们不难发现：任何一个ICG都可以通过把每个局势堪称一个顶点，对每个局势和它的子局势连一条有向边来抽象成这个”有向图游戏”。

3.解决方案(SG函数与SG定理)

现在我们假定给出两个游戏$G1$和$G2$。如果我们只知道单个游戏的$P$状态和$N$状态是无法正确的进行组合游戏$G1+G2$的。这是由于$P$状态和$P$状态的和总是$P$状态；$P$状态和$N$状态的和总是$N$状态；但是$N$状态和$N$状态的和的状态是无法确定的。

因此我们需要对两个状态进行推广。

1.SG函数(Sprague-Grudy’s Function)

首先我们引入$mex$函数的定义：

定义 $\mathrm{mex}$ 函数的值为不属于集合 $S$ 中的最小非负整数，即：

mex ⁡ ( S ) = min ⁡ { x } ( x ∉ S , x ∈ N ) \operatorname{mex}(S)=\min\{x\} \quad (x \notin S, x \in N) mex(S)=min{
x}(x∈/​S,x∈N)

例如 mex ⁡ ( { 0 , 2 , 4 } ) = 1 \operatorname{mex}(\{0, 2, 4\})=1 mex({
0,2,4})=1， mex ⁡ ( { 1 , 2 } ) = 0 \operatorname{mex}(\{1, 2\})=0 mex({
1,2})=0。

对于状态 $x$ 和它的所有 $k$ 个后继状态 $y_1,y_2,\dots ,y_k$，定义 $\mathrm{SG}$ 函数：
SG ⁡ ( x ) = mex ⁡ { SG ⁡ ( y 1 ) , SG ⁡ ( y 2 ) , … , SG ⁡ ( y k ) } \operatorname{SG}(x)=\operatorname{mex}\{\operatorname{SG}(y_1), \operatorname{SG}(y_2), \ldots, \operatorname{SG}(y_k)\} SG(x)=mex{
SG(y1​),SG(y2​),…,SG(yk​)}

2.SG定理(Sprague-Grudy’s Theorem)

根据$SG$函数，我们可以导出$SG$定理：对于由 $n$ 个有向图游戏组成的组合游戏，设它们的起点分别为 $s_1,s_2,\dots ,s_n$，则有定理：当且仅当 $\mathrm{SG}(s_1)\oplus \mathrm{SG}(s_2)\oplus \dots \oplus \mathrm{SG}(s_n)\ne 0$ 时，这个游戏是先手必胜的。

接下来，我们对$SG$定理的性质进行研究：

1. 所有的终结点所对应的顶点，其$SG$值为$0$，因为它的后继集合为空集。

   即：所有的终结点都是必败点

2. 对于一个$SG(X)=0$的顶点$X$，它的所有后继都无法满足$SG(y)!=0$。

   即：无论如何操作，从必败点（P点）都只能进入必胜点（N点）

3. 对于一个$SG(x)!=0$的顶点，必定存在一个后继点$y$满足$g(y)=0$

   从任何必胜点（$N$点）操作，至少有一种方法可以进入必败点（$P$点）//就是那种我们要走的方法。

3.应用

(1).将Nim游戏转换为有向图游戏

我们可以将一个有 $x$ 个物品的堆视为节点 $x$，则当且仅当 $y<x$ 时，节点 $x$ 可以到达 $y$。

那么，由 $n$ 个堆组成的 Nim 游戏，就可以视为 $n$ 个有向图游戏了。

根据上面的推论，可以得出 $\mathrm{SG}(x)=x$。再根据 SG 定理，就可以得出 Nim 和的结论了。

(2).关于步数的结论

1. 可选步数为$1-m$的连续整数，直接取模即可，$SG=x\%(m+1)$;
2. 可选步数为任意步，$SG(x)=x$;
3. 可选步数为一系列不连续的数，用$mex(计算每个节点的值)$

以将一个有 $x$ 个物品的堆视为节点 $x$，则当且仅当 $y<x$ 时，节点 $x$ 可以到达 $y$。

那么，由 $n$ 个堆组成的 Nim 游戏，就可以视为 $n$ 个有向图游戏了。

根据上面的推论，可以得出 $\mathrm{SG}(x)=x$。再根据 SG 定理，就可以得出 Nim 和的结论了。

(2).关于步数的结论

1. 可选步数为$1-m$的连续整数，直接取模即可，$SG=x\%(m+1)$;
2. 可选步数为任意步，$SG(x)=x$;
3. 可选步数为一系列不连续的数，用$mex(计算每个节点的值)$