（二）【数学建模】优劣解距离法（TOPSIS）

大家好，欢迎来到IT知识分享网。

（1）模型介绍

• TOPSIS法（Technique for Order Preference by Similarity to ideal Sulution）可翻译为逼近理想解排序法，国内简称为优劣解距离法。（优解：最大值；劣解：最小值）
• TOPSIS法是一种常用的综合评价方法，其能充分利用原始数据的信息，其结果能精确地放映各评价方案之间地差距。
• 层次分析法地一些局限性

差异太大，可能无法通过一致性检验

（2）TOPSIS应用例子：

排名越小越好，但评分越高越好，所以要进行修正。

问题：第一名与最后一名无论成绩为多少评分都是1和0，为什么要用上图的公式，不用下图的公式？

解释：

1>如果评价的人数很多，只有最前与最后两个有影响，无所谓。
2> 小明一个指标得分为零，但有其他指标弥补
3>…

指标类型不同，要进行统一处理：

$Z^{-}与Z^{+}$为每个指标的最小值，最大值
$D_i^{-}与D_i^{+}$为第i个评价对象的每个评价指标与最大值的距离之和。

（3）算法步骤

1）将原始矩阵正向化

<1>极小型到极大型

<2>中间型到极大型

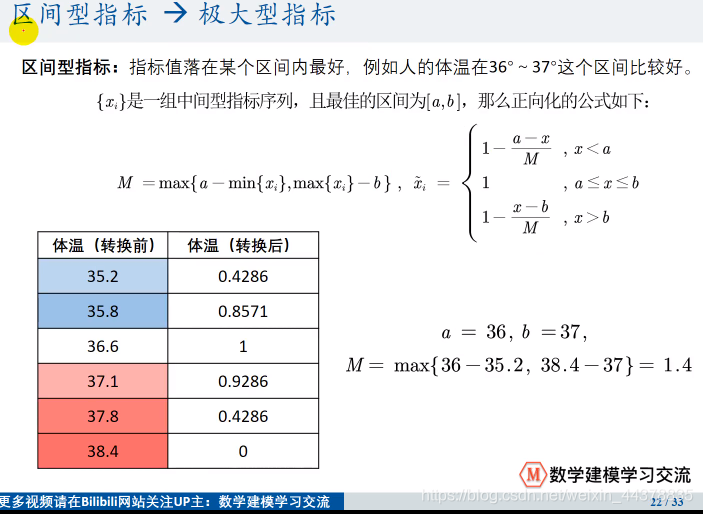
<3>区间型到极大型

修改: $M=max(|x_1-x_{best}|,|x_2-x_{best}|,...)$。

$|x_i-x_{best}|$越大，转换后值越小

2）正向化矩阵标准化

3）计算得分并归一化

$最后一行应该是：D_i^{+}越小$