浅谈 FHQ Treap

大家好，欢迎来到IT知识分享网。

浅谈 FHQ Treap

简单介绍

FHQ Treap,以下简写为 $fhq$，是一种treap(树堆)的变体，功能比treap强大。
$fhq$ 不需要通过一般平衡树的左右旋转来保持平衡，而是通过分裂 $split$和合并 $merge$ 来实现操作。

优点是比较好理解、代码短、上手快、可持久化

主要是不用像 $splay$ 一样旋来旋去。

Treap比较好玩的一点是，它整体是拥有二叉搜索树的性质，但是它的每一个节点都会有一个附加权值，它的附加权值是符合堆的性质。

这样我们可以明显看出，这棵树的形态(平衡与否)是由这个附加权值决定的。

那我们该如何取这个权值呢？随机！！

是的，我们每次都随机一个权值作为它的附加权值，那么它就大概是平衡的。

只需要两个基础操作，就可以达到splay的所有功能

前置操作

结构

对于每个树上节点开一个结构体，维护左儿子、右儿子、两个权值、还有子树中的节点个数。

然后给定一个树上的权值 $v$​ ，新建节点，还有更新子树大小 $update$。

struct fhq { 
    int l , r , v , t , sz; } tr[N]; void update (int x) { 
    tr[x].sz = 1 + tr[tr[x].l].sz + tr[tr[x].r].sz; } int new_pos (int v) { 
    tr[++pos].sz = 1; tr[pos].v = v; tr[pos].t = rnd (); return pos; } 

$rnd()$ 是随机数生成函数，需要搞一个预处理

std::mt19937 rnd(233); 

分裂 split

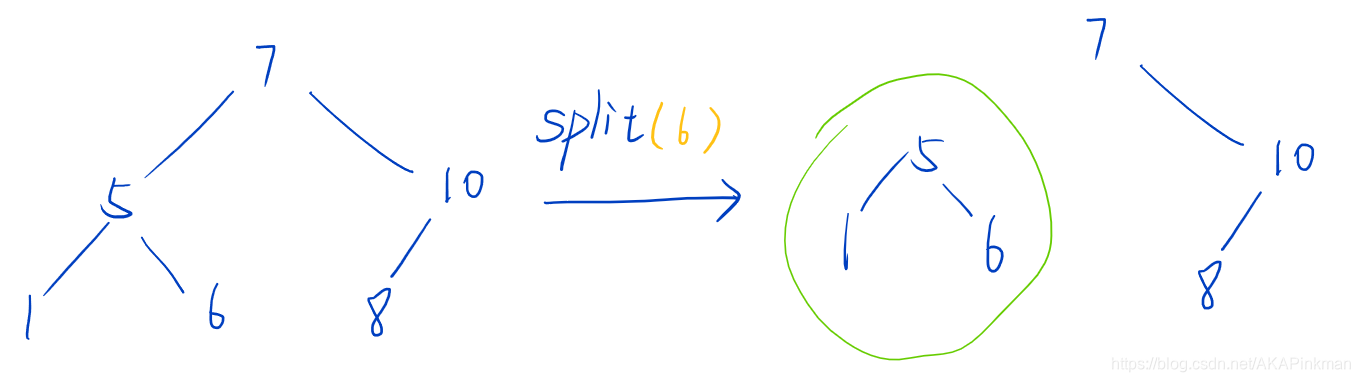
这个的主要思想就是把一个 $treap$ 按照一个权值 $v$ 分成两个。

把所有小于等于 $v$ 的分到一棵树中，把所有大于 $v$ 的分到另一棵树中，如下图。

可以对照代码感性理解一下

void split (int now , int k , int &x , int &y) { 
    if (now == 0) x = y = 0; else { 
    if (tr[now].v <= k) x = now , split (tr[now].r , k , tr[now].r , y); else y = now , split (tr[now].l , k , x , tr[now].l); update (now); } } 

合并 merge

$merge$ 操作按照堆权合并x,y两颗子树,合并前要保证x子树中的权值<y子树中的权值，如下图。

图中黄字为堆权

int merge (int x , int y) { 
    if (x == 0 || y == 0) return x + y; if (tr[x].t < tr[y].t) { 
    tr[x].r = merge (tr[x].r , y); update (x); return x; } else { 
    tr[y].l = merge (x , tr[y].l); update (y); return y; } } 

一般操作

Insert

插入一个权值为 $v$ 的点，把树按照 $v$ $split$ 成两个，再按照顺序合并。

split (rt , a , x , y); rt = merge (merge (x , new_pos (a)) , y); 

delete

删除权值为 $v$ 的点，需要 $split$ 两次。一次按照 $v$ 分成 $x,z$ ，一次把 $x$ 按照 $v-1$ 分成 $x,y$ ，那么 $y$ 的中间点就是 $v$ ，把 $y$ 的两个儿子直接合并也就相当于删除了 $v$ ，然后再按照顺序把其他节点合并就好了。

split (rt , a , x , z); split (x , a - 1 , x , y); y = merge (tr[y].l , tr[y].r); rt = merge (merge (x , y) , z); 

查询排名为 $x$ 的数

就是普通的查询，每次把 $x$ 和当前节点的左子树大小比较即可。

int kth (int now , int k) { 
    while (1) { 
    if (k <= tr[tr[now].l].sz) now = tr[now].l; else if (k == tr[tr[now].l].sz + 1) return now; else k -= tr[tr[now].l].sz + 1 , now = tr[now].r; } } 

查询 $v$ 的排名 rank

把原树 $split$ 按照 $v-1$ 成 $x,y$ ，$x$ 的大小 $+1$ 即为 $x$ 的排名。

split (rt , a - 1 , x , y); printf ("%d\n" , tr[x].sz + 1); rt = merge (x , y); 

查询 $x$ 的前驱 precursor

找前驱的话把原树按 $v-1$ $split$成 $x,y$，在 $x$ 里面找最大值。

split (rt , a - 1 , x , y); printf ("%d\n" , tr[kth (x , tr[x].sz)].v); rt = merge (x , y); 

查询 $x$ 的后继 successor

跟前驱类似。把原树按 $v$ $split$ 成 $x,y$，在 $y$ 里找最小值。

split (rt , a , x , y); printf ("%d\n" , tr[kth (y , 1)].v); rt = merge (x , y); 

版题

题目传送门

#include <bits/stdc++.h> #define fu(x , y , z) for(int x = y ; x <= z ; x ++) using namespace std; const int N = 5e5 + 5; std::mt19937 rnd(233); int pos , rt; struct fhq { 
    int l , r , v , t , sz; } tr[N]; void update (int x) { 
    tr[x].sz = 1 + tr[tr[x].l].sz + tr[tr[x].r].sz; } int new_pos (int v) { 
    tr[++pos].sz = 1; tr[pos].v = v; tr[pos].t = rnd (); return pos; } void split (int now , int k , int &x , int &y) { 
    if (now == 0) x = y = 0; else { 
    if (tr[now].v <= k) x = now , split (tr[now].r , k , tr[now].r , y); else y = now , split (tr[now].l , k , x , tr[now].l); update (now); } } int merge (int x , int y) { 
    if (x == 0 || y == 0) return x + y; if (tr[x].t < tr[y].t) { 
    tr[x].r = merge (tr[x].r , y); update (x); return x; } else { 
    tr[y].l = merge (x , tr[y].l); update (y); return y; } } int kth (int now , int k) { 
    while (1) { 
    if (k <= tr[tr[now].l].sz) now = tr[now].l; else if (k == tr[tr[now].l].sz + 1) return now; else k -= tr[tr[now].l].sz + 1 , now = tr[now].r; } } int main () { 
    int T , op , a , x , y , z; scanf ("%d" , &T); while (T --) { 
    scanf ("%d%d" , &op , &a); if (op == 1) { 
    split (rt , a , x , y); rt = merge (merge (x , new_pos (a)) , y); } else if (op == 2) { 
    split (rt , a , x , z); split (x , a - 1 , x , y); y = merge (tr[y].l , tr[y].r); rt = merge (merge (x , y) , z); } else if (op == 3) { 
    split (rt , a - 1 , x , y); printf ("%d\n" , tr[x].sz + 1); rt = merge (x , y); } else if (op == 4) printf ("%d\n" , tr[kth (rt , a)].v); else if (op == 5) { 
    split (rt , a - 1 , x , y); printf ("%d\n" , tr[kth (x , tr[x].sz)].v); rt = merge (x , y); } else { 
    split (rt , a , x , y); printf ("%d\n" , tr[kth (y , 1)].v); rt = merge (x , y); } } return 0; }