大家好,欢迎来到IT知识分享网。
文章目录
4.三次函数
三次函数即形如:
f ( x ) = a x 3 + b x 2 + c x + d , a ≠ 0 f(x)=ax^3+bx^2+cx+d,a\neq0 f(x)=ax3+bx2+cx+d,a=0
(1)对称性
三次函数图像是中心对称图形,对称中心为: ( − b 3 a , f ( − b 3 a ) ) (-\frac{b}{3a},f(-\frac{b}{3a})) (−3ab,f(−3ab))
P r a . 4.1 Pra.4.1 Pra.4.1
求证: f ( x ) = a x 3 + b x 2 + c x + d , a ≠ 0 f(x)=ax^3+bx^2+cx+d,a\neq0 f(x)=ax3+bx2+cx+d,a=0满足:
f ( x ) + f ( − 2 b 3 a − x ) = 2 f ( − b 3 a ) f(x)+f(-\frac{2b}{3a}-x)=2f(-\frac{b}{3a}) f(x)+f(−3a2b−x)=2f(−3ab)
- S o l u t i o n Solution Solution:证明略。
P r a . 4.2 Pra.4.2 Pra.4.2
设函数 f ( x ) = x 3 − 3 x 2 − x f(x)=x^3-3x^2-x f(x)=x3−3x2−x,设
t = ∑ i = 1 2021 f ( i 1011 ) t=\sum\limits_{i=1}^{2021}f(\frac{i}{1011}) t=i=1∑2021f(1011i)
求 t t t的值。
- S o l u t i o n Solution Solution: t = − 6063 t=-6063 t=−6063,利用对称性即可。
(2)根的数量问题
所谓根的问题,指一个三次函数与 x x x轴交点的个数。
对三次函数 f ( x ) = a x 3 + b x 2 + c x + d , a ≠ 0 f(x)=ax^3+bx^2+cx+d,a\neq0 f(x)=ax3+bx2+cx+d,a=0求导得:
f ′ ( x ) = 3 a x 2 + 2 b x + c f'(x)=3ax^2+2bx+c f′(x)=3ax2+2bx+c
令 f ′ ( x ) = 0 f'(x)=0 f′(x)=0,设 Δ = 4 ( b 2 − 3 a c ) > 0 \Delta=4(b^2-3ac)>0 Δ=4(b2−3ac)>0我们有:
x = − b ± b 2 − 3 a c 3 a x=\frac{-b\pm \sqrt{b^2-3ac}}{3a} x=3a−b±b2−3ac
设 x = x 1 , 2 , x 1 < x 2 x=x_{1,2},x_1<x_2 x=x1,2,x1<x2
为了讨论方便,假设 a > 0 a>0 a>0,那么:
f ( x ) f(x) f(x)在 ( − ∞ , x 1 ) (-\infty,x_1) (−∞,x1)递增, ( x 1 , x 2 ) (x_1,x_2) (x1,x2)递减, ( x 2 , + ∞ ) (x_2,+\infty) (x2,+∞)递增
因此: f ( x ) f(x) f(x)的根的情况为
| 条件 | 根的情况 |
|---|---|
| f ( x 1 ) f ( x 2 ) < 0 f(x_1)f(x_2)<0 f(x1)f(x2)<0 | 3 3 3个实数根 |
| f ( x 1 ) f ( x 2 ) > 0 f(x_1)f(x_2)>0 f(x1)f(x2)>0 | 1 1 1个实数根 |
| f ( x 1 ) f ( x 2 ) = 0 f(x_1)f(x_2)=0 f(x1)f(x2)=0 | 2 2 2个实数根 |
(3)根的求解问题
三次方程的求解遵循:猜根法。
一般特殊解为 x = ± 1 , ± 2 x=\pm1,\pm2 x=±1,±2等。
P r a . 4.3 Pra.4.3 Pra.4.3
求方程 x 3 − 6 x 2 + 11 x − 6 = 0 x^3-6x^2+11x-6=0 x3−6x2+11x−6=0的根
- S o l u t i o n Solution Solution:猜根得 x = 1 x=1 x=1是原方程的根
分解为: x 3 − 6 x 2 + 11 x − 6 = ( x − 1 ) ( x 2 − 5 x + 6 ) = ( x − 1 ) ( x − 2 ) ( x − 3 ) x^3-6x^2+11x-6=(x-1)(x^2-5x+6)=(x-1)(x-2)(x-3) x3−6x2+11x−6=(x−1)(x2−5x+6)=(x−1)(x−2)(x−3)
因此原方程的根为: x 1 = 1 , x 2 = 2 , x 3 = 3 x_1=1,x_2=2,x_3=3 x1=1,x2=2,x3=3
(4)切线问题
遵循“飞哥圆盘”定理。
“左右三,线上二,上下一。”
结论如下:
| 位置 | 切线条数 |
|---|---|
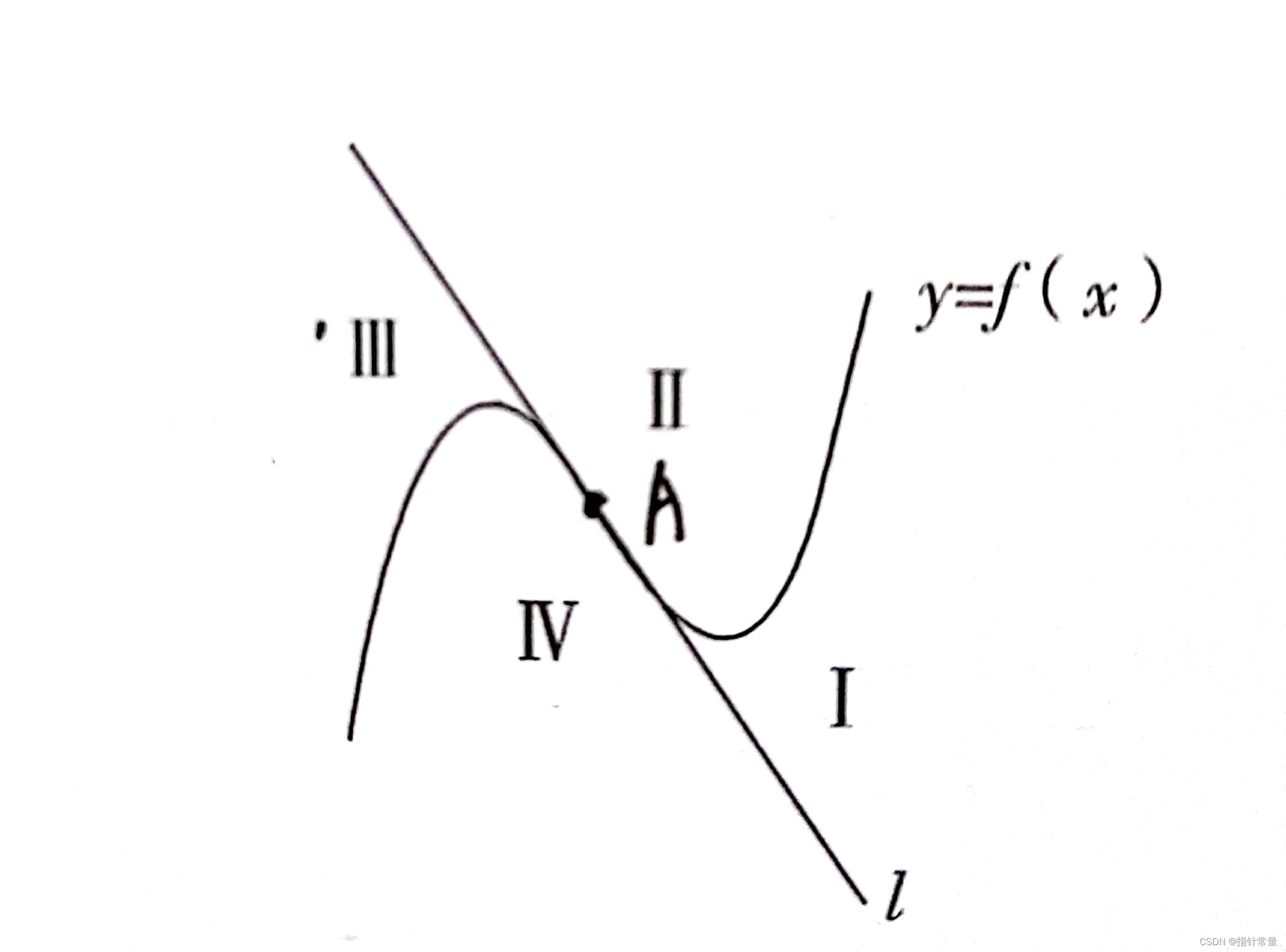
| 过区域Ⅰ、Ⅲ内的点作 y = f ( x ) y=f(x) y=f(x)的切线 | 3 3 3 |
| 过区域Ⅱ、Ⅳ内的点以及对称中心作 y = f ( x ) y=f(x) y=f(x)的切线 | 1 1 1 |
| 过切线 l l l或者 y = f ( x ) y=f(x) y=f(x)图像(除去对称中心)上的点作 y = f ( x ) y=f(x) y=f(x)的切线 | 2 2 2 |
P r a . 4.4 Pra.4.4 Pra.4.4
已知函数 f ( x ) = x 3 − x . f(x)=x^3-x. f(x)=x3−x.
(1)求曲线 y = f ( x ) y=f(x) y=f(x)在点 M ( t , f ( t ) ) M(t,f(t)) M(t,f(t))处的切线方程;
(2)设 a > 0 a>0 a>0,如果过 N ( a , b ) N(a,b) N(a,b)可作曲线 y = f ( x ) y=f(x) y=f(x)的三条切线,求证:
− a < b < f ( a ) -a<b<f(a) −a<b<f(a)
- S o l u t i o n Solution Solution:略。
P r a . 4.5 Pra.4.5 Pra.4.5
已知函数 f ( x ) = 2 x 3 − 3 x . f(x)=2x^3-3x. f(x)=2x3−3x.
(1)求 f ( x ) f(x) f(x)在区间 [ − 2 , 1 ] [-2,1] [−2,1]上的最大值
(2)若过点 P ( 1 , t ) P(1,t) P(1,t)存在三条直线与曲线 y = f ( x ) y=f(x) y=f(x)相切,求 t t t的取值范围;
(3)问过点 A ( − 1 , 2 ) , B ( 2 , 10 ) , C ( 0 , 2 ) A(-1,2),B(2,10),C(0,2) A(−1,2),B(2,10),C(0,2)分别存在几条直线与曲线 y = f ( x ) y=f(x) y=f(x)相切?
- S o l u t i o n Solution Solution:最大值 2 \sqrt 2 2; t ∈ ( − 3 , − 1 ) t\in(-3,-1) t∈(−3,−1);分别: 3 , 2 , 1 3,2,1 3,2,1条直线。
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/154878.html