证明圆周角定理

大家好，欢迎来到IT知识分享网。

1.圆周角和圆心角的概念

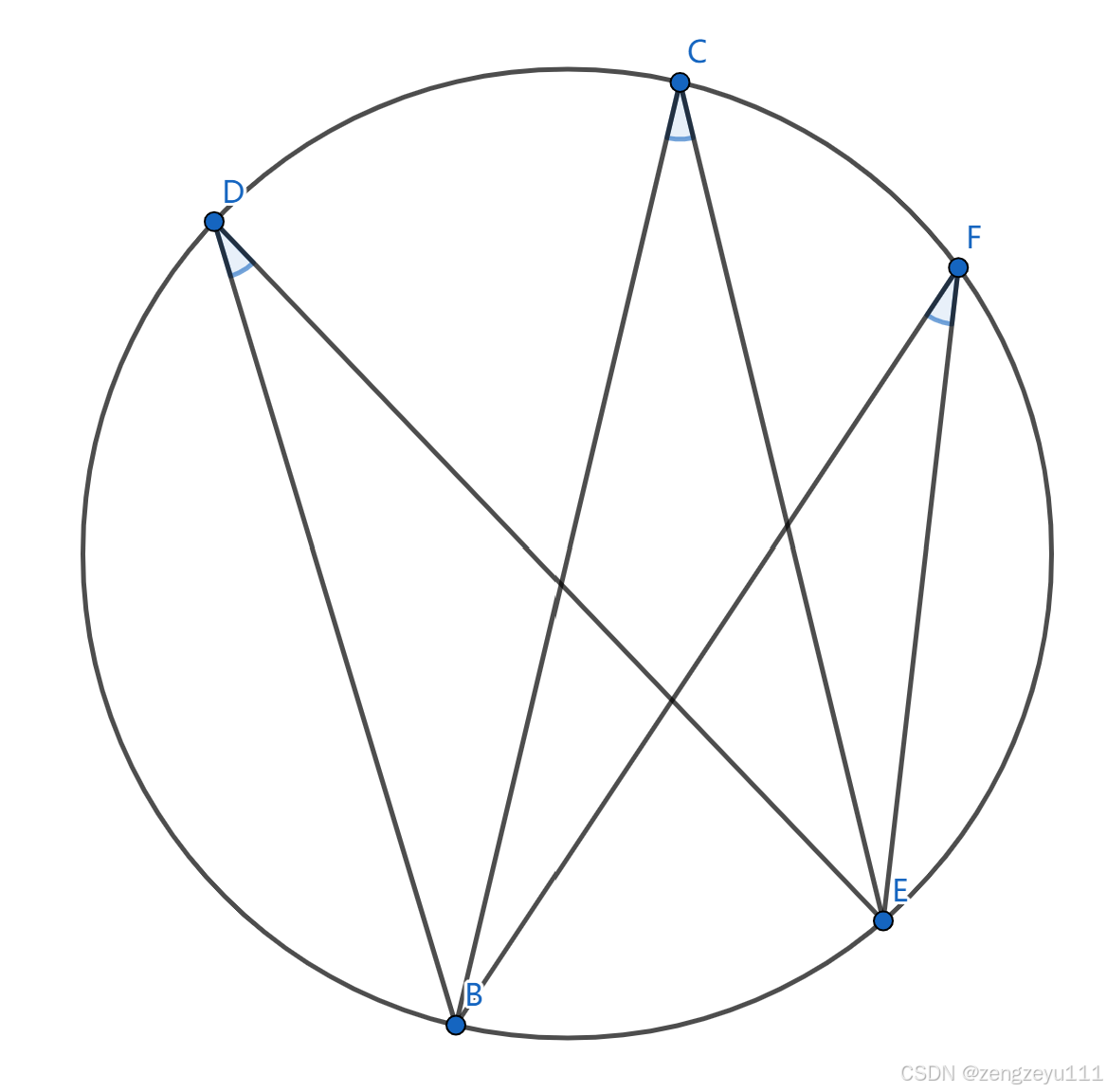
         圆周角是指角的顶点在圆周上，角的两边与圆周相交的角，如下图：

        在图中\(\angle D\),\(\angle C\)和\(\angle F\)就是圆周角。

        圆心角是指顶点在圆心上，两条边与圆周相交的角，如：

 如上图\(\angle BAE\)就是圆心角。

2.证明圆周角定理

        圆周角定理为同一个弧对应的圆周角是圆心角的\(\frac{1}{2}\)。在下图中弧CBE对应的公式为：\(\angle D=\frac{1}{2} \angle A\)

        接下来来证明圆周角定理，分为三种情况

情况一：

        圆周角的一边和圆心角的一边处于同一条直线上：

\(\because \angle CAD+\angle C+\angle D=180^{\circ } \)

 \(\therefore \angle CAD=180^{\circ }-\angle C-\angle D\)

\(\therefore \angle BAD=180^{\circ }-\angle CAD=180^{\circ}-\left (  180^{\circ}-\angle C – \angle D\right ) \)

\(\therefore \angle BAD=\angle C + \angle D\)

\(又\because \angle C = \angle D\)

\(\therefore \frac{1}{2} \angle BAD=\angle C\)

\(这就证明了\)

$$\angle C=\frac{1}{2}\angle A$$

情况二：

        圆周角和圆心角的任何一边都不重合，如下：

我们发现，可以沿着两个角的顶点做一条线，即连接点D和点A，如下： 

 就把它分成两个情况一，便可以轻松证明。

情况三：

        圆周角顶点在圆心角以外，如图:

我们可以连接EA并延长到圆周上并命名与圆周的交点为F，如：

 \(根据情况一，可以证明\frac{\angle FEC}{\angle FAC}=\frac{\angle FED}{\angle FAD} =\frac{1}{2}\)

\(又因\angle CAD = \angle FAD – \angle FAC,\angle CED = \angle FED-\angle FEC\)

\(则,\frac { \angle CED} { \angle CAD}=\frac{\angle FED-\angle FEC}{\angle FAD-\angle FAC}= \frac{\angle FED-\angle FEC}{2\left ( \angle FED-\angle FEC \right ) } = \frac{1}{2}\)

\(即可证明{\color{Red} {\angle CAD = \frac{1}{2}\angle CED}}\)