大家好,欢迎来到IT知识分享网。



原理
- 勒贝格积分的基本思想:勒贝格积分是对值域进行划分 ,不像黎曼积分那样对定义域(积分区间)进行划分。它将函数值相近的点归为一类,计算这些点构成集合的测度,再乘以对应的函数值并求和取极限。对于狄利克雷函数,其值域只有0和1两个值,就分别找出函数值为0和1的点集,即无理数集和有理数集,然后根据它们的测度和对应函数值来计算积分。
- 测度的作用:测度是勒贝格积分的基础概念,用于衡量集合的 “大小” 。在狄利克雷函数积分计算中,有理数集测度为0起到关键作用。因为有理数集是可数集,根据勒贝格测度的定义和性质,可数集的测度为0 。而函数在有理数集上取值为1 ,但由于其测度为0 ,在积分计算中这部分贡献为0 ;函数在无理数集上取值为0 ,所以最终积分结果为0 。

如果当x是无理数的时候,将狄利克雷函数的值改为x而不是0,狄利克雷函数还是勒贝格可积吗?
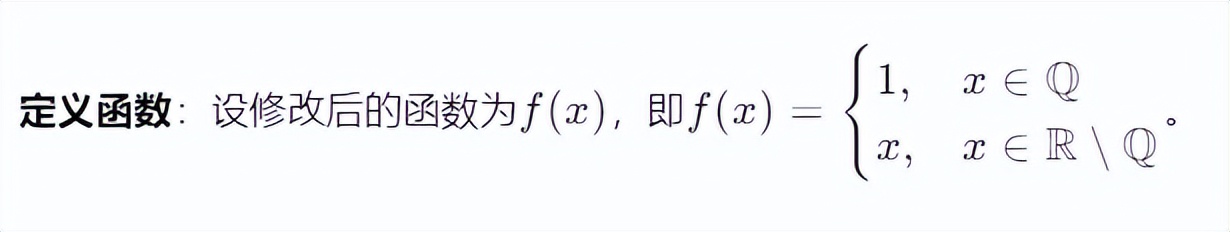



免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/183719.html

