算法基础：矩阵运算 实现原理和应用场景

大家好，欢迎来到IT知识分享网。

矩阵运算是数学和计算机科学中的一个核心概念，其实现原理和应用场景广泛而多样。以下从实现原理和应用场景两个方面进行详细说明：

一、矩阵运算的实现原理

1.基本定义与性质
矩阵是由行和列组成的矩形数组，可以表示为二维数组。矩阵的基本运算包括加法、减法、乘法、数乘、转置、求逆等。这些运算的实现依赖于矩阵的定义和相关性质，例如矩阵加法要求两个矩阵的维度相同，而矩阵乘法则需要满足左矩阵的列数与右矩阵的行数相等。

线性代数第二章矩阵及其运算详解

2.算法实现

• 加法与减法：通过逐元素相加或相减实现，时间复杂度为 O(n2)，其中 n 是矩阵的维度。

人工智能之数学(一) —— 矩阵的概念与运用

• 乘法：矩阵乘法的核心是内积运算，即一个矩阵的行与另一个矩阵的列进行点积计算。对于两个 m×n 和 n×p 的矩阵，其乘积的时间复杂度为 O(mnp)。优化算法如 Strassen 算法和 Coppersmith-Winograd 算法可以进一步降低复杂度。

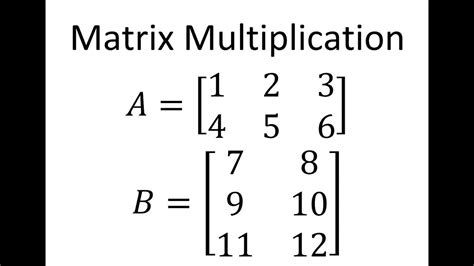
How To Multiply 3×3 And 3×2 Matrices – Michael Ferguson’s Multiplying

第2章 矩阵 PowerPoint Presentation, free download

3.硬件加速
矩阵运算在现代计算中常通过硬件加速实现。例如，GPU 和专用矩阵运算芯片（如 NVIDIA 的 GPGPU）利用并行计算能力显著提升性能。此外，FPGA 和 VLSI 系统中也采用专门的矩阵运算工具链（如 MOD 工具）来优化设计。

4.编程语言实现
在编程语言中，矩阵运算可以通过库函数实现。例如，Python 的 NumPy 库提供了高效的矩阵运算功能，而 JavaScript 通过合理的算法设计也能实现高效的矩阵运算。

Numpy Matrix Multiplication – NumPy v1.17 Manual (Updated)

二、矩阵运算的应用场景

1.数据挖掘与机器学习
矩阵运算是数据挖掘和机器学习的基础工具。例如，在聚类分析（如 K-means 算法）中，通过矩阵运算提取数据特征并进行关联分析。在深度学习中，神经网络的权重更新和激活函数计算均依赖于矩阵乘法和加法。

2.图像处理
图像处理中，矩阵常用于表示像素值或滤波器操作。例如，卷积操作可以通过矩阵乘法实现，从而加速图像滤波和特征提取。

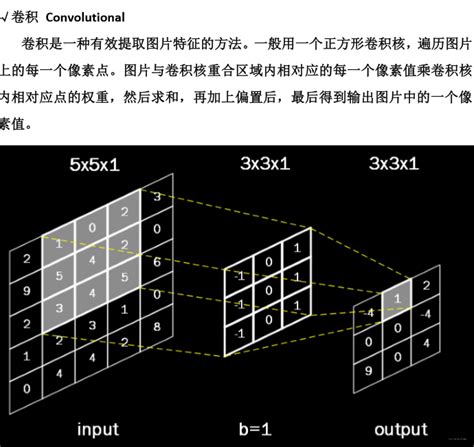
深度学习实践Tensorflow搭建卷积

3.科学计算与工程应用
矩阵运算是解决线性方程组、动力学分析和控制理论问题的重要工具。例如，在机械强度分析和经济建模中，通过矩阵运算可以简化复杂的计算过程。

7.3 一般性线性方程组求解

4.优化算法
矩阵运算在优化算法中也有广泛应用，如拉格朗日乘子法和 SVD 分解用于求解最优化问题。

拉格朗日乘子法

5.通信与信号处理
在通信领域，矩阵运算用于信号编码、解码和传输优化。例如，盲源分离技术通过矩阵分解实现信号分离。

6.游戏开发与图形学
在游戏开发中，矩阵用于表示空间变换（如旋转、缩放和投影），从而实现复杂的图形渲染。

Stardust · 理论物理初阶】 篇七 · 诺特定理：对称性与守恒律之羁绊

总结

矩阵运算是数学和计算机科学中的基础工具，其实现原理涵盖了基本运算规则、算法优化和硬件加速等多个方面。在实际应用中，矩阵运算广泛应用于数据挖掘、机器学习、图像处理、科学计算、优化算法和通信等领域，是现代技术不可或缺的一部分