相关性分析 | 透彻理解关系强度 Minitab 实操示范

大家好，欢迎来到IT知识分享网。

大家好，我是玫森，

在日常工作和生活中，我们常常会遇到需要探究事物之间关系的情况。例如：

HR会问：影响员工离职的关键原因，是工资还是发展空间？

商家会琢磨：影响产品出餐率的因素，是烤箱温度的不稳定，还是订单量的突然暴增？

产品设计人员：影响汽车产品受欢迎的关键，是价格、还是动力等？

零售店老板会：影响冰激凌销售量的原因，是温度升高，还是学生暑期放假？

工程师会问：影响产品推拉力的原因，是烤箱温度，还是胶量多寡？

我们会问：体重增加了是运动量减少了， 还是进食量增加了？

这些问题的核心，都离不开对两个或多个因素之间关系的研究，我们今天要探讨的主题 – 相关性。

01

散点图：直观洞察变量关系

当我们想要初步了解两个变量X和Y之间的关系时，散点图是一个非常实用的工具。

简单来说，散点图就是将X变量的值放在横轴，Y变量的值放在纵轴，然后将每一组对应的X和Y值作为一个点绘制在坐标系中。通过观察这些点的分布形态，我们能够定性地判断X和Y之间的关系。

如果点的分布呈现出从左下角到右上角的趋势，那就意味着X和Y之间可能存在正相关关系。比如说，随着广告投放量（X）的增加，产品的销售量（Y）也随之上升。相反，如果点的分布是从左上角到右下角，那么X和Y之间可能是负相关关系，就像商品价格（X）提高时，其销量（Y）反而下降。要是点在坐标系中毫无规律地随机分布，那很大程度上说明X和Y之间不存在明显的线性相关关系，比如人的身高（X）和每天使用手机的时长（Y），二者之间就很难找到直接的关联。

散点图帮助我们快速、直观地了解变量之间是否存在某种联系，为进一步的深入分析提供了重要的线索。

上面“脂肪百分比与BMI 体重指数”的散点图，可目视直观的看出脂肪百分比随着BMI 体重指数的增加而上升，反映两个变量之间的关系是正相关。

仅仅通过散点图定性地判断变量之间有关系还不够，我们往往还想知道这种关系究竟有多强，有多深？这时候就需要引入相关性系数r 。

02

相关性系数r：量化关系强度

我们想知道上面“脂肪百分比与BMI 体重指数”量化的关系程度，Excel 和Minitab 均可操作（医学方面常用的是SPSS统计分析软件，我们制造企业中较多用的是Minitab统计分析软件），下面Minitab 操作示范：

结果：Correlations 显示=0.863，也就是说，通过散点图，我们不仅知道了它们之间存在正向相关，且它们之间的关系强度为0.863（有了量化的数值了）

这里的Correlations 指数是指的是r 值？ 什么是r值？

相关性系数r是一个能够定量衡量两个变量之间线性相关程度的指标，它的取值范围在-1到1之间。

相关系数的特征 ：正负号：表示相关方向，正值表示正相关，负值表示负相关。

• |r|越趋于1，表示线性相关越强；|r|越趋于0，表示线性相关越弱。

• 若|r|=1，为完全线性相关

• r=1，为完美完全正线性相关。

• r=-1，为完美完全负线性相关。

• 若r >0，表示两个变量存在正相关。

• 若r< 0，表示两个变量存在负相关。

• 若r = 0，表示两个变量不存在线性相关关系，可能存在抛物线相关（非线性关系）

相关性系数r在很多情况下又特指皮尔逊相关系数（Pearson correlation coefficient）。

03

皮尔逊相关系数

1.）定义:相关系数是最早由统计学家卡尔. 皮尔逊设计的统计指标，是研究变量之间线性相关程度的量，一般用字母 r, ρx,y或Corr(X,Y) 表示。由于研究对象的不同，相关系数有多种定义方式，较为常用的是皮尔逊相关系数。

需要说明的是，皮尔逊相关系数并不是唯一的相关系数，但是最常见的相关系数，无特殊说明时相关系数一般指的都是皮尔逊相关系数。

使用该相关的前提是双变量均为符合正态分布的连续型变量，因此需要提前做正态性检验，对于不符合正态分布的变量，可以取对数后重新检验正态性，或者使用Spearman相关分析或者KendallTau-b相关分析。

2.） 关注的点: 在进行分析时，我们重点需要关注的点：

• 是否存在相关性，相关性的强弱有多少
• 是否存在相关性是根据
• P值来判断，P值<0.05 则具有相关性、P值>0.05则不具有相关性
• 相关系数(r)的取值范围在[-1,1]之间，绝对值越靠近1, 则说明相关性越强，|r|＜0.3为低度相关，0.3<|r|<0.5为中度相关，0.5<|r|<0.8为较强相关，r|>0.8为高度相关

3.) 计算方法

计算方式基于两个变量的协方差和标准差。

公式中：

X, Y是两个随机变量

分子：Cov(X,Y) 表示所有数据点与各自均值之差的乘积之和，为X与Y的协方差 ，计算两个标准化变量之间的协方差。协方差表示两个变量共同变化的趋势，如果它们同时增加或减少，那么它们的协方差为正；如果它们相互变化的方向不一致，则协方差为负。

分母：Var[X]为X的方差，Var[Y]为Y的方差。

由于上述相关系数是根据样本数据计算出来的，所以上述相关系数又称为样本相关系数（用r来表示）。若相关系数是根据总体全部数据计算的，称为总体相关系数，记为ρ。

由于存在抽样的随机性和样本较少等原因，通常样本相关系数不能直接用来说明两总体（即两变量）是否具有显著的线性相关关系，因此还必须进行显著性假设检验。下面带大家认识显著性检验的两种判定方式。

04

线性相关关系：显著性假设判定

相关系数显著性检验用于判断样本中观察到的相关关系是否在总体中真实存在，其核心是通过假设检验验证相关系数的统计显著性。具体流程包含假设建立、相关系数计算、统计量计算、p值确定及结果判定等关键步骤，最终依据p值与显著性水平的比较得出检验结论。

这里额外说明的一点是：相关性系数的总体显著性检验使用t检验，原因在于其抽样分布的特性与t分布的适用条件相匹配

1.）t检验的核心目的：

我们通过样本计算出相关系数r后，需要检验“总体相关系数ρ是否为0”（即判断样本的r是否由随机误差导致，而非总体真的存在相关性）。若能拒绝“ρ=0”的原假设，则认为r具有统计显著性。

2.) t检验适用的关键前提：

小样本场景：当样本量较小时（尤其n<30），r的抽样分布无法直接用正态分布近似，但符合自由度为n-2的t分布（n为样本量）。

统计量的构造：此时可构造t统计量：

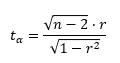
该统计量在原假设（ρ=0）成立时，恰好服从自由度为n-2的t分布，因此可通过t检验来判断r的显著性。

简言之，由于在“总体无相关（ρ=0）”的假设下，样本相关系数r的抽样分布符合t分布的特征，因此用t检验来完成其显著性检验是自然且合理的选择。

3. ）假设检验基本步骤：

1.）提出假设：

o 原假设H₀：总体变量间无线性相关，相关系数ρ=0，

o 备择假设H₁：总体变量间线性显著相关，相关系数ρ≠01。

2.）确定显著性水平α（显著性判断标准）：通常选择0.05或0.01作为显著性水平

当p < α时拒绝H₀，说明相关系数具有统计显著性，如p=0.03<0.05时，可认为变量间存在真实相关。

当p ≥ α时接受H₀，例如p=0.12>0.05时，样本相关可能由随机误差导致。

3.）计算样本相关系数r：使用样本数据计算出表征相关强度的r值。

4.）计算t统计量：t = r√(n-2)/√(1-r²)，其中n是样本大小。

5.）结果判定（通常最简单的判定方式看P值）：

查t分布表确定临界值：若|t|>临界值，则拒绝H0，说明相关关系显著，反之不显著。

或计算P值：通过t统计量计算P值，判断其是否小于显著性水平α。

回到上面案例Minitab 实操 快速判定显著性结果：

结果呈现：

P值判定：p值接近于0，p<0.05，拒绝“总体变量间无线性相关，相关系数ρ=0”的原假设，线性显著相关.

写在最后：

“相关性系数”是一个宽泛的概念，除了皮尔逊(Pearson)相关系数，还有斯皮尔曼(Spearman)相关系数、肯德尔(Kendall)相关系数等，它们适用于不同的数据类型或场景（比如斯皮尔曼系数更适合非正态分布或有序分类数据）。但通常如果没有特别说明，提到“相关性系数r”时，大多指的是皮尔逊相关系数。

先是通过散点图，直观判断两个变量 X 和 Y 有没有关联；接着借助皮尔逊（Pearson）相关系数 r ，量化它们关系的紧密程度。最后，利用样本相关系数 r 做假设检验 ，来推断两个样本对应的总体系数ρ是不是真有显著关系。希望今天的分享能对大家有所帮助。