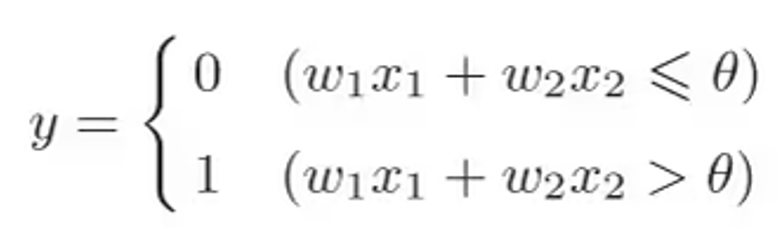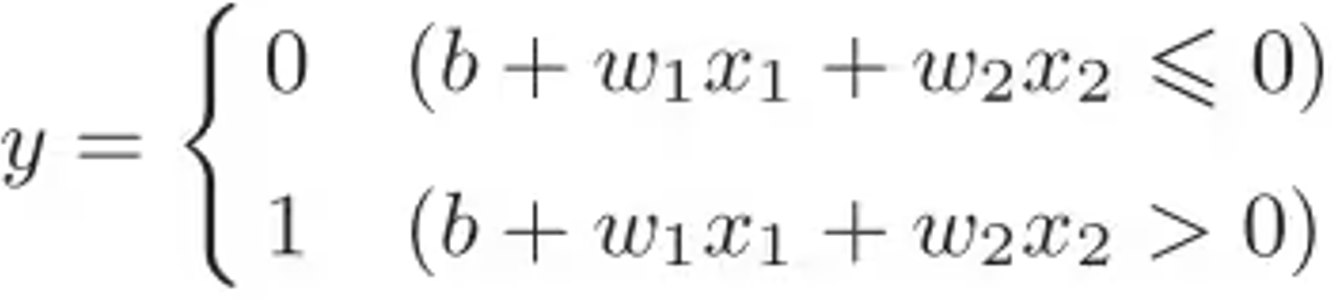【AI】机器学习——感知器

大家好，欢迎来到IT知识分享网。

4.4 感知器

4.4.1 概念

1957 年，美国康奈尔大学航天实验室的心理学家弗兰克·罗森布拉特(Frank Roseblatt)受到赫布理论的启发，提出了著名的“感知器（perceptron）”模型——第一个用算法精确定义的人工神经网络，只有一个神经元

解决二分类问题的监督学习算法，属于 线性分类模型——判别模型

感知机与人工神经网络

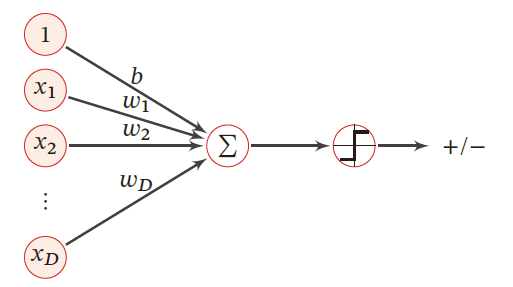
由输入层和输出层组成

• 输入层负责接收外界信号
• 输出层是MP神经元，即阈值逻辑函数

  每个输入信号都以一定权重 $\omega$（突触），偏置 $b$（阈值）被送入MP神经元（激活函数），MP神经元利用符号将特征的线性组合映射为分类输出 $+1$ ，$-1$

关于偏置（阈值的理解）

偏置用于衡量感知器触发的难易程度，当 $\theta =-b$ 时，二者是等价的

模型思想

目标：求出将训练数据进行线性划分的分离超平面

基本思想：错误驱动的在线学习算法 ——导入误分类的损失函数，利用梯度下降法对损失函数极小化，求得感知机模型

输入：$x\in \mathcal{X}\subseteq R^n$ 表示实例的特征向量， y ∈ Y = { + 1 , − 1 } y\in \mathcal{Y}=\{+1, -1\} y∈Y={
+1,−1}

输出：$\hat{\omega }$ ，$\hat{b}$

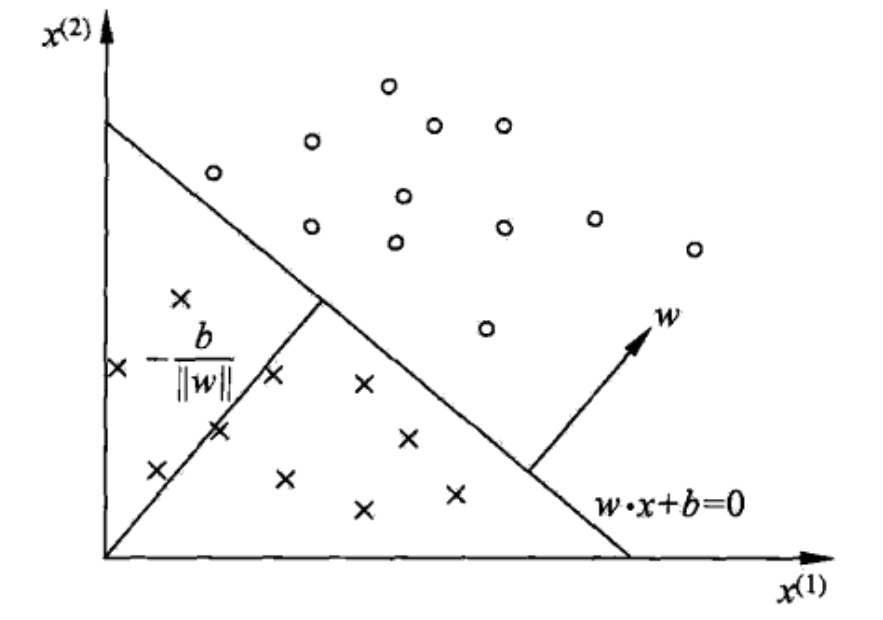
• 上图中超平面 $S:{\omega }_1{x}^{(1)}+{\omega }_2{x}^{(2)}+b=0$ ，这个超平面将特征空间分为 $+1,-1$ 类

4.4.2 策略

损失函数的定义，并将 $J(\omega )$ 最小化

数据集的线性可分性

对于数据集 $D$ ，若存在某个超平面 $S$ ：${\omega }^{T}x+b=0$ ，将数据正负两类完全划分到超平面两侧

• 对于正例：$y_i=+1$ ，有 ${\omega }^{T}x+b>0$
• 对于负例：$y_i=-1$ ，有 ${\omega }^{T}x+b<0$

学习策略

目标 ：假设数据集 $D$ 线性可分，找到将数据集 $D$ 正负两例完全正确分开的超平面 $S$，即确定参数 $\hat{\omega },\hat{b}$

损失函数的构造

可选择

• 误分类点的总数，但不关于 $\omega ,b$ 可导，是离散的
• 误分类点到超平面 $S$ 的距离和

点 $x_t$ 到平面 $S$ 的总距离
$$\frac{{\omega }^T{x}_t+b}{\Vert \omega {\Vert }_2}$$
对于误分类点有
$$y_t\cdot ({\omega }^T{x}_t+b)<0⟺-y_t\cdot ({\omega }^T{x}_t+b)>0$$
对于误分类点，到超平面的几何距离为
$$-\frac{1}{\Vert \omega {\Vert }_2}{y}_t\cdot ({\omega }^T{x}_t+b)$$
若所有误分类点集合为 $M$ ，则误分类点到 $S$ 的距离和为
$$-\frac{1}{\Vert \omega {\Vert }_2}\sum _{x_t\in M}{y}_t\cdot ({\omega }^T{x}_t+b)$$
故将感知机（损失函数）定义为经验风险函数
$$R_{emp}(f)=L(\omega ,b)=-\sum _{x_t\in M}{y}_t\cdot ({\omega }^T{x}_t+b)$$
策略为 在假设空间中选取使损失函数 $L(\omega ,b)$ 最小的模型参数 $\omega ,b$

• 损失函数非负
• 误分类点数量越少越好
• 误分类点离超平面越近越好
• $L(\omega ,b)$ 是连续可导的

关于距离的解释

• $-\frac{1}{\Vert \omega {\Vert }_2}{y}_t\cdot ({\omega }^T{x}_t+b)$ 为 几何距离
• $-y_t\cdot ({\omega }^T{x}_t+b)$ 为 函数距离

几何距离的系数 $\frac{1}{\Vert \omega {\Vert }_2}$ 可以抵消系数同时放大的影响，如 $aX+bY+c=0$ 与 $2aX+2bY+2c=0$

• 但会增加梯度下降法计算的复杂度

PLA的目标是使误分类点个数最小，$\frac{1}{\Vert \omega {\Vert }_2}$ 对分类结果无影响，故在PLA中损失函数不带系数 $\frac{1}{\Vert \omega {\Vert }_2}$

4.4.3 算法

用随机梯度下降法，求解损失函数最优化问题

PLA算法原始形式

输入：训练数据集
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯   , ( x N , y N ) } ， x i ∈ X ⊆ R n , y i ∈ Y = { + 1 , − 1 } , i = 1 , 2 , ⋯   , N D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}，\\ x_i\in \mathcal{X}\subseteq R^n,y_i\in \mathcal{Y}=\{+1,-1\},i=1,2,\cdots,N D={(x1​,y1​),(x2​,y2​),⋯,(xN​,yN​)}，xi​∈X⊆Rn,yi​∈Y={
+1,−1},i=1,2,⋯,N
输出：$\hat{\omega },\hat{b}$

模型
$$f(x)=sign({\omega }^{T}x+b)=\{\begin{array}{ll}+1& ,{\omega }^{T}x+b>0\\ -1& ,{\omega }^{T}x+b<0\end{array}$$
策略
$$arg\underset{\omega ,b}{\min }\mathcal{L}(\omega ,b)=arg\underset{\omega ,b}{\min }-\sum _{x_t\in M}{y}_t\cdot ({\omega }^T{x}_t+b)$$
步骤

1. 选取随机的 ${\omega }_0,b_0$ ，其中权重可以初始化为0或比较小的随机数
2. 在训练集中选数据 $(x_i,y_i)$ ，将误分类点作为训练数据，即满足 ${\omega }^T{x}_i+b<0$ 的条件的点
   $$\begin{gathered} {\omega }^{[t+1]}\leftarrow {\omega }^{[t]}-\eta \frac{\partial \mathcal{L}}{\partial \omega }={\omega }^{[t]}+\eta y_t{x}_t \\ {b}^{[t+1]}\leftarrow b^{[t]}-\eta \frac{\partial \mathcal{L}}{\partial b}=b^{[t]}+\eta y_t \end{gathered}$$
   
3. 转至 $2$ 步，直至 $D$ 中无误分类点

感知器通过传递函数确定输出，神经元之间通过权重传递信息，权重的变化则根据误差来进行调节

损失函数的梯度下降法

$$\{\begin{array}{l}{▽}_{\omega }\mathcal{L}(\omega ,b)=-\sum _{x_t\in M}{y}_t{x}_t\\ {▽}_b\mathcal{L}(\omega ,b)=-\sum _{x_t\in M}{y}_t\end{array}$$

前提是误分类点集合是固定的 ，才可进行梯度下降法最优化
$$\{\begin{array}{l}\omega \leftarrow \omega -\eta {▽}_{\omega }\mathcal{L}\\ b\leftarrow b-\eta {▽}_b\mathcal{L}\end{array}$$
这种做法：

• 计算量大
• 且调整参数 $\omega ,b$ 后，误分类点集可能会发生变化，故用随机梯度下降法

直观理解

当一个样本点被误分类时，调整 $\omega ,b$ 的值，使超平面 $S$ 向该误分类点的一侧移动，减少该误分类点与 $S$ 的距离，直至超平面越过此点（分类正确）

PLA例题

$$\begin{gathered} x_1=(3,3{)}^T,y_1=+1 \\ {x}_2=(4,3{)}^T,y_2=+1 \\ {x}_3=(1,1{)}^T,y_3=-1 \end{gathered}$$

1. 取初值，${\omega }_0=\left(\begin{array}{r}0\\ 0\end{array}\right)$ ，$b_0=0$ ，$\eta =1$
2. 对 $x_1=(3,3{)}^T$ ，有 $y_1({\omega }_1^{[0]}{x}_1^{(1)}+{\omega }_2^{[0]}{x}_1^{(2)}+b^{[0]})=0$
3. 对 $x_2=(4,3{)}^T,({\omega }_1^{[1]}{x}_2+{\omega }_2^{[1]}{x}_2+b^{[1]})y_2>0$ ，正确分类

   $x_3=(1,1{)}^T,({\omega }_1^{[1]}{x}_3+{\omega }_2^{[1]}{x}_3+b^{[1]})y_3<0$ ，误分类。用 $(x_3,y_3)$ 更新模型参数
   $$\{\begin{array}{l}{\omega }^{[2]}\leftarrow {\omega }^{[1]}-\eta \frac{\partial L}{\partial \omega }={\omega }^{[1]}+\eta y_3{x}_3=\left(\begin{array}{r}3\\ 3\end{array}\right)+(-1)\left(\begin{array}{r}1\\ 1\end{array}\right)=\left(\begin{array}{r}2\\ 2\end{array}\right)\\ b^{[1]}\leftarrow b^{[0]}-\eta \frac{\partial L}{\partial b}=b^{[0]}+\eta y_3=1+1\cdot (-1)=0\end{array}$$
   有线性模型
   $${\omega }_1^{[2]}{x}_1+{\omega }_2^{[2]}{x}_2=0⟺2x_1+2x_2=0⟺x_1+x_2=0$$
   
   
   

4. 对 $(x_1,y_1),(x_2,y_2),(x_3,y_3)$ 代入线性模型，反复迭代

PLA算法收敛性

[Novikoff, 1963]证明了当 输入数据线性可分 时，感知器学习算法能够在有限次的迭代后收敛，可以得到一个将训练数据集完全正确划分的超平面 $S$

证明

1. 上界
   $$\begin{array}{rl}\Vert {\omega }^{[T]}{\Vert }^2& =\Vert {\omega }^{[T-1]}+y_T{x}_T{\Vert }^2\\ & =\Vert {\omega }^{[T-1]}{\Vert }^2+\Vert y_T{x}_T{\Vert }^2+2y_T{\omega }^{[T-1]}{x}_T\\ & \because y_T{\omega }^{[T-1]}{x}_T\le 0\\ & \le \Vert {\omega }^{[T-1]}{\Vert }^2+\Vert y_T{x}_T{\Vert }^2\\ & \le \Vert {\omega }^{[T-2]}{\Vert }^2+\Vert y_{T-1}{x}_{T-1}{\Vert }^2+\Vert y_T{x}_T{\Vert }^2\\ & \cdots \\ & \le \sum _{t=1}^T\Vert y_t{x}_t{\Vert }^2\end{array}$$
   令 R 2 = max ⁡ t { ∥ y t x t ∥ 2 } = max ⁡ t { ∥ x t ∥ 2 } R^2=\max\limits_{t} \{\Vert y_tx_t\Vert^2\}=\max\limits_{t} \{\Vert x_t\Vert^2\} R2=tmax​{
   ∥yt​xt​∥2}=tmax​{
   ∥xt​∥2}
   
   

   有 $\Vert {\omega }^{[T]}{\Vert }^2\le T{R}^2$

2. 下界

   一定存在 $\Vert {\omega }_{\ast }\Vert =1$ 的超平面 ${\omega }_{\ast }x=0$ ，将数据完全正确划分
   $$\begin{array}{rl}\Vert {\omega }^{[T]}{\Vert }^2& =\Vert {\omega }_{\ast }{\Vert }^2\cdot \Vert {\omega }^{[T]}{\Vert }^2\\ & \ge \Vert {\omega }_{\ast }^T{\omega }^{[T]}{\Vert }^2\\ & =\Vert {\omega }_{\ast }^T\sum _{t=1}^T{y}_t{x}_t{\Vert }^2\\ & =\Vert \sum _{t=1}^T{\omega }_{\ast }^T{y}_t{x}_t{\Vert }^2\end{array}$$
   令 γ 2 = min ⁡ t { ∥ y t ( ω ∗ T x t ) ∥ 2 } = min ⁡ t { ∥ ω ∗ T x t ∥ 2 } \gamma^2=\min\limits_{t}\{\Vert y_t(\omega_*^Tx_t)\Vert^2\}=\min\limits_{t}\{\Vert \omega_*^Tx_t\Vert^2\} γ2=tmin​{
   ∥yt​(ω∗T​xt​)∥2}=tmin​{
   ∥ω∗T​xt​∥2} ，即距离划分超平面最近的点
   
   

   有 $\Vert {\omega }^{[T]}{\Vert }^2\ge T^2{\gamma }^2$

非参数化性

感知器没有做出任何关于固有分布形式的假设，通过不同分布重叠区域产生的误差来运行

• 当输入数据是非高斯分布时，算法依然能够正常工作

自适应性

只要给定训练数据集，算法就可以基于误差修正自适应地调整参数而无需人工介入

局限

• 感知器不能解决以异或为代表的线性不可分问题

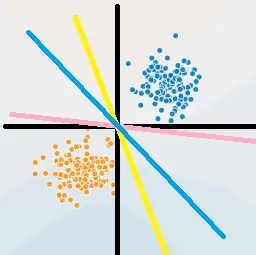
  划分这四个点就是一个二分类问题。这个问题不是一个线性分类问题，因为找不到任何一条直线能将将正方形中两组对角线上的顶点分为一类。

  1969 年，新科图灵奖得主马文·明斯基和他的麻省理工学院同侪塞默尔·帕波特合著了《感知器：计算几何简介》（Perceptrons: An Introduction to Computational Geometry）一书，系统论证了感知器模型的两个关键问题。

  第一，单层感知器无法解决以异或为代表的线性不可分问题；

  第二，受硬件水平的限制，当时的计算机无法完成训练感知器所需要的超大的计算量。

• 感知器对样本顺序敏感，每次迭代的顺序不一致时，找到的分割超平面也不一致

  感知机存在许多解，依赖于初值的选择

  

• 在数据集线性可分时，感知器虽然可以找到一个超平面把两类数据分开，但并不能保证其泛化能力

4.4.4 感知器改进

PLA解决线性不可分问题——对偶形式

原始PLA分析

在原始 PLA 算法中， ${\omega }_0=0$ ， $b_0=0$ ，$\mathcal{L}(\omega ,b)=-\sum _{x_t\in M}{y}_t({\omega }^T\cdot x_t+b)$ ，采用随机梯度下降算法，取一个误分类点 $(x_t,y_t)$ 作为学习数据，$\eta \in (0,1]$ 为学习率
$$\{\begin{array}{l}{\omega }^{[t+1]}\leftarrow {\omega }^{[t]}-\eta \frac{\partial \mathcal{L}}{\partial \omega }={\omega }^{[t]}+\eta y_t{x}_t\\ b^{[t+1]}\leftarrow b^{[t]}-\eta \frac{\partial \mathcal{L}}{\partial b}=b^{[t]}+\eta y_t\end{array}$$
可见

• $\omega$ 更新至于误分类点有关

  某个点使用次数越多，距超平面越近，越难正确分类

• 假设 $(x_t,y_t)$ 被误分类 $n_t$ 次，则 $\omega$ 在 $(x_t,y_t)$ 上的累积量为
  $$\{\begin{array}{l}\delta {\omega }_t\leftarrow n_t\eta y_t{x}_t={\alpha }_t{y}_t{x}_t\\ \delta b_t\leftarrow n_t\eta y_t={\alpha }_t{y}_t\end{array}$$
  且对于正确分类的点 $n_t=0$ ，故原始PLA参数可表示为
  $$\{\begin{array}{l}\omega \leftarrow \sum _{i=1}^N{n}_i\eta y_i\cdot x_i\\ b\leftarrow \sum _{i=1}^N{n}_i\eta y_i\end{array}$$
  
  
  

PLA对偶形式

输入：
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯   , ( x N , y N ) } , x i ∈ X ⊆ R n , y i ∈ Y = { + 1 , − 1 } , i = 1 , 2 , ⋯   , N D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\},x_i\in \mathcal{X}\subseteq R^n,y_i\in \mathcal{Y}=\{+1,-1\},i=1,2,\cdots,N D={(x1​,y1​),(x2​,y2​),⋯,(xN​,yN​)},xi​∈X⊆Rn,yi​∈Y={
+1,−1},i=1,2,⋯,N
$\eta \in (0,1]$

模型
$$\begin{array}{rl}f(x)& =sign[(\sum _{i=1}^N{n}_i\eta y_i{x}_i{)}^T\cdot x+\sum _{i=1}^N{n}_i\eta y_i]\\ & =sign[\sum _{i=1}^N{\alpha }_i{y}_i(x_i\cdot x{)}^T+b]\end{array}$$
输出 ：$\alpha ,b$ $\alpha =\left(\begin{array}{r}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_N\end{array}\right)$ ，${\alpha }_i=n_i\eta$ ，$n_i$ 为 $(x_i,y_i)$ 被误分类的次数

步骤

1. $\forall n_i=0$ ，即 $\alpha =0,b=0$
2. 选取误分类点 $(x_t,y_t)$ ，若 $y_t[\sum _{i=1}^N{n}_i\eta y_i(x_i^T\cdot x_t)+\sum _{i=1}^N{n}_i\eta y_i]\le 0$ ，则令
   $$\begin{gathered} n^{[t+1]}\leftarrow n^{[t]}+1 \\ {\alpha }^{[t+1]}\leftarrow {\alpha }^{[t]}+\eta \\ {\omega }^{[t+1]}\leftarrow {\omega }^{[t]}+\eta y_t{x}_t \\ {b}^{[t+1]}\leftarrow b^{[t]}+\eta y_t \end{gathered}$$
   
3. 转至 $2.$ 直至没有误分类点

由于样本点只以内积形式出现，可计算 Gram矩阵
$$G=[x_i\cdot x_j{]}_{N\times N}=\left[\begin{array}{cccc}(x_1,x_1)& (x_1,x_2)& \cdots & (x_1,x_N)\\ (x_2,x_1)& (x_2,x_2)& \cdots & (x_2,x_N)\\ ⋮& ⋮& \ddots & ⋮\\ (x_N,x_1)& (x_N,x_2)& \cdots & (x_N,x_N)\end{array}\right]$$

优点

可预先计算存储 Gram 矩阵，提高计算速度

可通过 Gram 矩阵引入核函数，有 $K(x,z)=\varphi (x)\cdot \varphi (z)$ ，可解决非线性分类问题

多层感知器

解决异或问题的思路相当简单，就是将单层感知器变成多层感知器

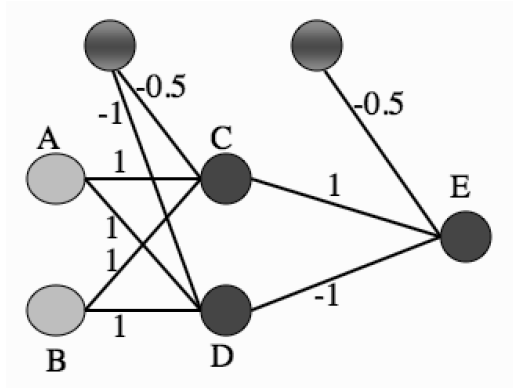
假定两个输入节点 A 和 B 的二进制输入分别为 1 和 0，则根据图中的权重系数可以计算出神经元 C 的输入为 0.5，而神经元 D 的输入为 0。在由 C 和 D 构成的隐藏层中，由于 C的输入大于 0，因而符号函数使其输出为 1；由于 D 的输入等于 0，符号函数则使其输出为0。在输出节点的神经元 E 上，各路输入线性组合的结果为 0.5，因而 E 的输出，也是神经网络整体的输出，为 1，与两个输入的异或相等。

多层感知器（multilayer perceptron）包含一个或多个在输入节点和输出节点之间的隐藏层（hidden layer），除了输入节点外，每个节点都是使用非线性激活函数的神经元

在不同层之间，多层感知器具有全连接性，即任意层中的每个神经元都与它前一层中的所有神经元或者节点相连接，连接的强度由网络中的权重系数决定。

多层感知器是一类前馈人工神经网络（feedforward neural network）。网络中每一层神经元的输出都指向输出方向，也就是向前馈送到下一层，直到获得整个网络的输出为止。

训练步骤

确定给定输入和当前权重下的输出，再将输出和真实值相减得到误差函数，最后根据误差函数更新权重

反向传播

在训练过程中，虽然信号的流向是输出方向，但计算出的误差函数和信号传播的方向相反，也就是向输入方向传播的，正因如此，这种学习方式得名反向传播（backpropagation）。

反向传播算法通过求解误差函数关于每个权重系数的偏导数，以此使误差最小化来训练整个网络

参数平均感知器

根据定理，若间隔 $\gamma$ 越大，则收敛越快，但感知器不能保证找到的判别函数是最优的，可能导致过拟合

感知器学习到的权重向量和训练样本的顺序相关。在迭代次序上排在后面的错误样本比前面的错误样本，对最终的权重向量影响更大

比如有1000个训练样本，在迭代100个样本后，感知器已经学习到一个很好的权重向量．在接下来的899个样本上都预测正确，也没有更新权重向量．但是，在最后第1000个样本时预测错误，并更新了权重．这次更新可能反而使得权重向量变差

为了提高感知器的泛化能力，可以在感知器学习过程中的 $T$ 个权重向量保存，并赋予每个权重向量 ${\omega }_t$ 一个置信系数 $c_t(1\le t\le T)$ ，最终的分类结果通过这 $T$ 个不同权重的感知器投票决定——投票感知器

令 ${\tau }_t$ 为第 $t$ 次更新权重 ${\omega }_t$ 时的迭代次数，则权重 ${\omega }_t$ 的置信系数 $c_t$ 设置为从 ${\tau }_t$ 到 ${\tau }_{t+1}$ 之间间隔的迭代次数，即 $c_t={\tau }_{t+1}-{\tau }_t$

置信系数 $c_t$ 越大，说明权重 ${\omega }_t$ 在之后的训练过程中正确分类的样本数越多，越值得信赖，故投票感知器的形式为
$$\hat{y}=sign\left(\sum _{t=1}^T{c}_{t}sign({\omega }_t^{T}x)\right)$$
投票感知器虽然提高了感知器的泛化能力，但需要保存 $T$ 个权重向量，在实际操作中会带来额外的开销。

• 每次迭代都需要更新 $\overline{\omega }$

因为 $\overline{\omega }$ 与 $\omega$ 都是稠密向量，所以更新操作比较费时

扩展到多分类

蒲公英书3.4.4