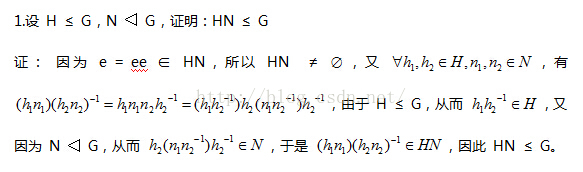大家好，欢迎来到IT知识分享网。
正规子群的定义：
群 H 为 G 的子群，若对任意的 a ∈ G，都有 aH = Ha，则称 H 为 G 的一个正规子群，记作 H ◁ G。
正规子群例子：
1.特殊线性群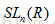 
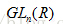
是一般线性群 
的正规子群。
2.交错群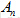 
是对称群 
的正规子群。
命题1. 设 H 是 G 的子群，则 H 为 G 的正规子群当且仅当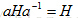 
对任意 a ∈ G 成立。
正规子群的性质：
1.设 H 是 G 的正规子群，K 是 G 包含 H 的子群，则 H 是 K 的正规子群。
2.H 是 群 G 的正规子群当且仅当 H 的所有共轭子群等于 H。
3.设 H 和 K 为群 G 的子群，则
（1）.若 H 和 K 都是群 G 的正规子群，则 H 与 K 的乘积 HK 也是 G 的正规子群
（2）.若 H 和 K 都是群 G 的正规子群，则 H 与 K 的交 HK 也是 G 的正规子群
（3）.若 H 和 K 都是群 G 的正规子群，并且 H 与 K 的交为 { e }，则 hk = kh 对任意的 h ∈ H 和任意的 k ∈ K 成立
正规子群的练习：
免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/118613.html
