最长公共子序列（LCS）

大家好，欢迎来到IT知识分享网。

一、相关概念

        区分子序列和子串

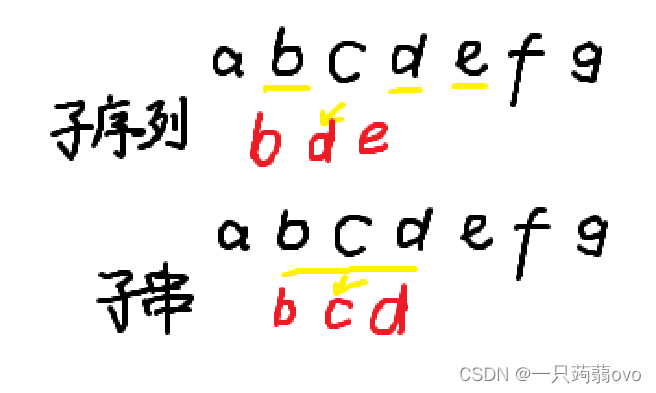
        子序列：给定序列中零个或多个元素去掉后的结果，也可以说从给定序列中选取几个元素的结果（有顺序）。

        子串：给定串中任意个连续的字符组成的子序列为该串的子串。

         最长公共子序列：两个字符串中，公共且最长的子序列。

举例： （最长公共子序列不唯一，但序列长度是相同的）

二、LCS 算法过程解析

        1.算法思路过程

  LCS 的特征：

    对于任意两个字符串数组 s1,s2, 公共子序列 s3

                若 s1[i] 与 s2[j] 相同， 则此时公共子序列s3末尾 s[x] 一定为 s1[i]

        原因： 若s3末尾s3[x] 不为 s1[i]，则 s3的最后一项一定是 s1[a]=s2[b] !=s3[x] （或者为空）, 那么一定可以把 s1[i] 接在 s3 的末尾，从而得到更长的公共子序列.        

                若 s1[i] 与 s2[j] 不相同, 则此时公共子序列 要么为 s1[0]~s1[i-1] 与 s2[0]~s2[j] 的公共子序列  要么为  s1[0]~s1[i] 与 s2[0]~s2[j-1] 的公共子序列，取二者最长的子序列即可

        根据上述特征,可以得出简单的计算最长公共子序列的长度的递推公式

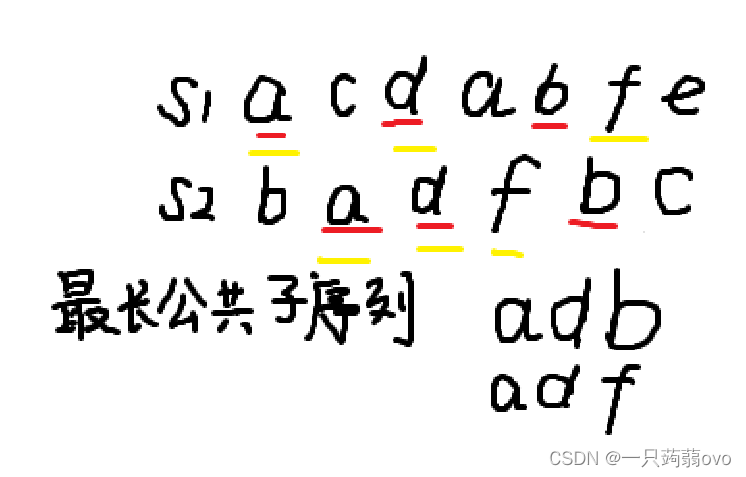
        对于上述例子 s1={a,c,d,a,b,f,e}     s2={b,a,d,f,b,c}

  为了防止数组越界,统一将字符串数组右移一位（即s1[1]为起始字符）

                                用红笔标出了 s1[i] == s2[j] 的情况

该图表示任何一个 i , j 都能找到对应的最长公共子序列对应 

三、通过LCS数组反推求出最长公共子序列

1.算法思路过程        

两个序列的最长公共子序列不一定只有一个，也存在多个的情况，这里主要讲述如何找出其中的一个LCS最长公共子序列.

        从最后一个元素 C[l1][l2] 反推出 s1 s2 的LCS

     s1 [ l1 ] != s2 [ l2 ]  则直接倒推至 c [ l1 – 1 ] [ l2 ] 或者 c [ l1 ] [ l2 – 1 ]   （需判断 c [ l1 ] [ l2 ] 的值来源于哪个）

                            若存在 c [ l1 – 1 ] [ l2 ] 与 c [ l1 ] [ l2 – 1 ] 相等的情况,则只需选择往哪个方向, 以后同样遇到这种分支情况,仍需要往该方向. 

        s1 [ l1 ] == s2 [ l2 ]  则直接倒推至 c [ l1 – 1 ] [ l2-1 ] ,并记录下此处的字符作为公共子序列

这里以图示说明其中的某一种情况.

       四、算法时间复杂度的分析

                需要通过两层for循环记录 c [ i ] [ j ] ,因此时间复杂度为 

#include<stdio.h> #include<string.h> #include<iostream> using namespace std; char ch1[1001],ch2[1001],s[10001]; char c1[1001],c2[1001]; int c[1001][1001]; int sum; int main() { scanf("%s",c1); scanf("%s",c2); int l1=strlen(c1),l2=strlen(c2); for(int i=0;i<l1;i++) ch1[i+1]=c1[i]; // 将字符数组右移一位 for(int j=0;j<l2;j++) ch2[j+1]=c2[j]; for(int i=1;i<=l1;i++) for(int j=1;j<=l2;j++) { if(ch1[i]==ch2[j]) // 若相同时，直接从 i-1，j-1 处推导 c[i][j]=c[i-1][j-1]+1; else // 不相同时 从 i-1，j 和 i，j-1 处推导 c[i][j]=max(c[i-1][j],c[i][j-1]); } while(c[l1][l2]!=0) // 反推最长公共子序列 { if(ch1[l1]==ch2[l2]) // 记录相同情况，保存进 子序列中 { s[sum++]=ch1[l1]; l1--,l2--; } if(ch1[l1]!=ch2[l2]) // 不相同情况，判断往哪个方向移动 { if(c[l1][l2-1]!=c[l1-1][l2]) // 先判断不同，则不必考虑方向 { if(c[l1][l2]==c[l1][l2-1]) // 判断从哪个推导到 i，j { l1=l1; l2=l2-1; } else if(c[l1][l2]==c[l1-1][l2]) { l1=l1-1; l2=l2; } } else // 相同情况，则固定方向移动 { l1=l1-1; // l2=l2; } } } for(int i=sum-1;i>=0;i--) printf("%c",s[i]); // 倒推出 最长公共子序列 return 0; } 

参考博文     最长公共子序列(LCS) 过程图解_最长子序列-CSDN博客