大家好,欢迎来到IT知识分享网。
第五章:SFM与三维重建
1. 三维重建简述
- 计算机视觉包含两个基本方向,物体识别和三维重建。图像识别的突破性进展源自于2012年卷积神经网络(CNN)的兴起。在此之前,计算机视觉的核心研究方向是三维重建。因为在当时,对于图像的特征提取主要是通过三维重建的方法来定义和实现的。自2012年以来,图像的特征便逐渐由神经网络来自动学习。
- 三维重建的应用是很广泛的,对于自动驾驶、VR、AR等应用领域应用来讲,三维重建是核心技术,并且实时三维重建是必然趋势,因为我们生活在三维空间里,必须将虚拟世界恢复到三维,我们才可以和环境进行交互。所以仅仅研究识别肯定是不够的,计算机视觉下一步必须走向三维重建,并且把三维重建和识别融为一体。
- 古建筑修复与重建是三维重建的一个具有代表性的应用,比如近期被烧毁的巴黎圣母院,如果通过三维模型网址进行数字重建,应该能够达到原汁原味还原其真实面貌的目的。目前在我们的三维重建项目中,名胜古迹的三维电子存档是很重要的一部分。从表面上看,三维重建似乎没有自动驾驶那么复杂,其实它比自动驾驶更难,因为自动驾驶的三维感知是给车识别,而VR、AR中的三维重建场景是提供给人类感知的,所以对三维重建的结果要求非常高。
总体来讲,三维重建是计算机视觉的灵魂。
2. 对极几何
2.1 对极几何简述
先思考一个问题:用两个相机在不同的位置拍摄同一物体,如果两张照片中的景物有重叠的部分,我们有理由相信,这两张照片之间存在一定的对应关系,本节的任务就是如何描述它们之间的对应关系,描述工具是对极几何 ,它是研究立体视觉的重要数学方法。
- 对极几何(Epipolar Geometry)描述的是两幅视图之间的内在射影关系,与外部场景无关,只依赖于摄像机内参数和这两幅试图之间的的相对姿态
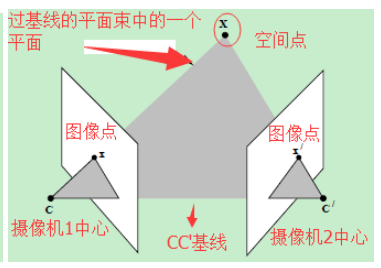
- 提到对极几何,一定是对二幅图像而言,对极几何实际上是“两幅图像之间的对极几何”,它是图像平面与以基线为轴的平面束的交的几何(这里的基线是指连接摄像机中心的直线),以下图为例:对极几何描述的是左右两幅图像(点x和x’对应的图像)与以CC’为轴的平面束的交的几何
2.2 五点共面约束
- 点x、x’与摄像机中心C和C’是共面的,并且与空间点X也是空面的,这5个点共面于平面π。这是一个最本质的约束,即5个点决定了一个平面π。
- 由该约束,可以推导出一个重要性质:由图像点x和x’反投影的射线共面,并且,在平面π上,在搜索点对应中,该性质非常重要。
2.3 几个相关概念
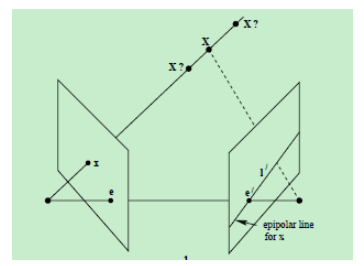
- 对极点(epipole):摄像机的基线与每幅图像的交点;即下图中的点e和e’(对极点=基线与像平面的交点=光心在另一幅图像中的投影)
- 对极线(epipolar line):对极平面与图像的交线;即下图中的直线l和l’(对极线=对极平面与像平面的交线)
- 对极平面(epipolar plane):任何包含基线的平面都称为对极平面,或者说是对极平面束中的平面;即下图中的平面就是一个对极平面
(对极平面=包含基线的平面)
2.4 对应点的约束
问题:当只知道图像点x,那么它的对应点x’如何约束?
- 点x和x’一定位于平面π上,而平面π可以利用基线CC’和图像点x的反投影射线确定
- 点x’又是右侧图像平面上的点,所以,点x’一定位于平面π与右侧图像平面的交线l’上
- 直线l’为点x的对极线,也就是说,点x的对应点x’一定位于它的对极线上
3. 两种矩阵
这里先说一下关于矩阵中的秩之前一直不是很理解,知乎上的解答:
- 「秩」是图像经过矩阵变换之后的空间维度
「秩」是列空间的维度
前者更直观,而后者是前者的原因- 1 「秩」是图像经过矩阵变换之后的空间维度
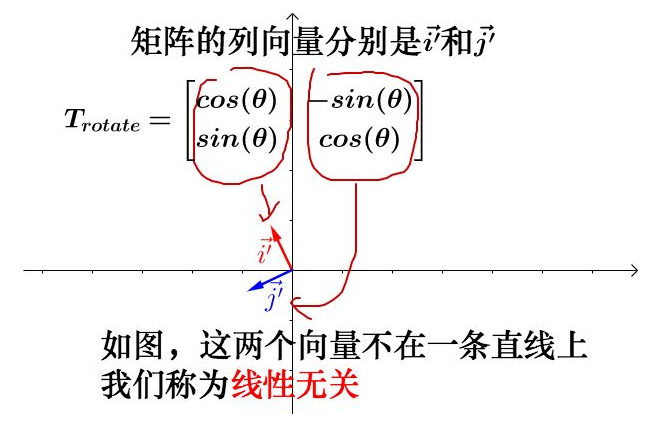
通过旋转矩阵进行变换:
[ c o s θ − s i n θ s i n θ c o s θ ] \begin{gathered} \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix} \end{gathered} [cosθsinθ−sinθcosθ]
因此,旋转矩阵的「秩」为2。
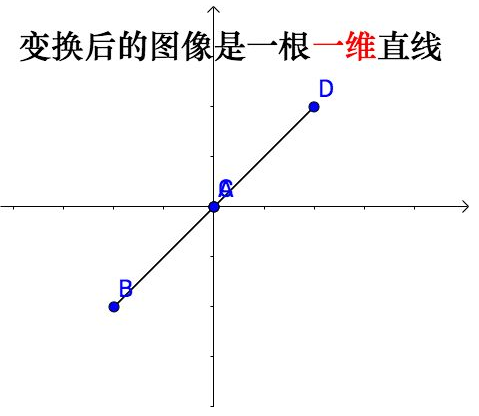
通过矩阵 [ 1 − 1 1 − 1 ] \begin{gathered} \begin{bmatrix} 1 & -1 \\ 1 & -1 \end{bmatrix} \end{gathered} [11−1−1]进行变换:
因此,此矩阵的「秩」为1通过矩阵 [ 0 0 0 0 ] \begin{gathered} \begin{bmatrix} 0 & 0 \\ 0 & 0\end{bmatrix} \end{gathered} [0000] 进行变换:
因此,此矩阵的秩为0
所以,秩是图像经过矩阵变换之后的空间维度。 - 1 「秩」是图像经过矩阵变换之后的空间维度
可以从另一维度来解释为什么
2 「秩」是列空间的维度
- 2.1 什么是列空间
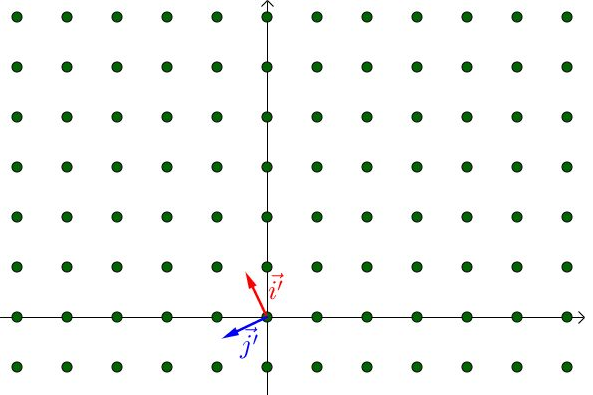
我们通过旋转矩阵来解释什么是列空间:
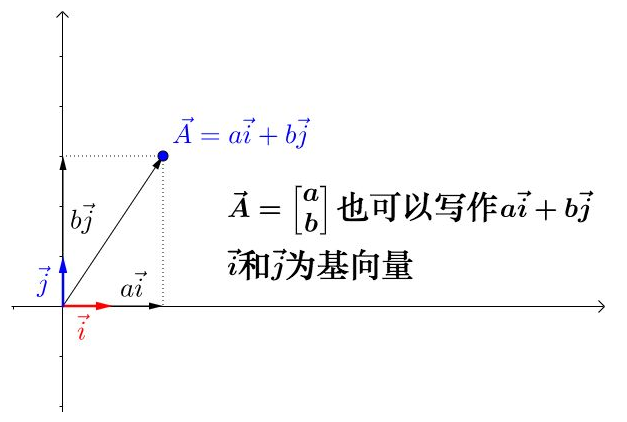
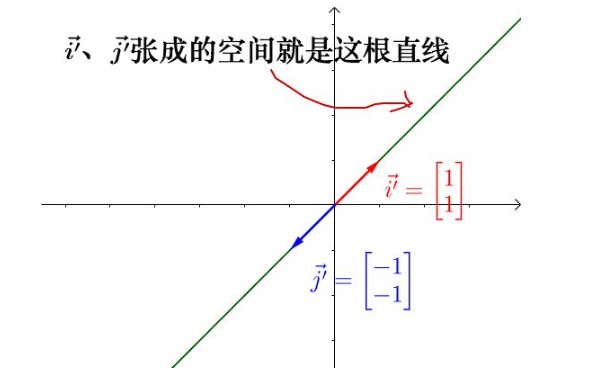
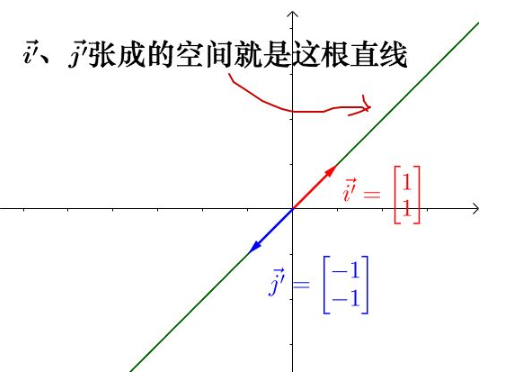
通过改变 a i ′ ⃗ + b j ′ ⃗ \vec{ai’}+\vec{bj’} ai′+bj′的值,可以用 [公式] 来表示二维平面上的所有点:
所以,列空间就是矩阵的列向量所能张成的空间(即能通过 a i ′ ⃗ + b j ′ ⃗ \vec{ai’}+\vec{bj’} ai′+bj′来表示)的空间
列空间的维度就是秩,旋转矩阵的列空间是二维的,所以秩就为2
那么这种定义方式怎么和之前说的秩是图像经过矩阵变换之后的空间维度联系起来呢?
- 2.2 矩阵的变换目标是列空间
有一个矢量
矩阵变换的其实是基
2.3 两种定义方式的联系
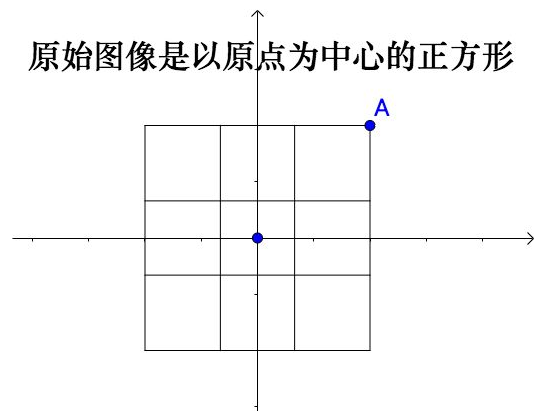
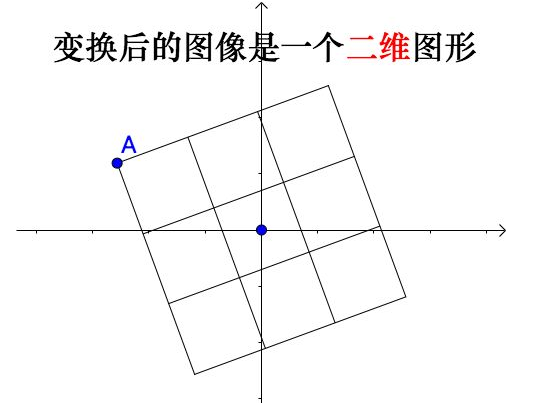
用旋转矩阵对二维的正方形进行线性变换,实际上是一个二维空间到另外一个二维空间的变换:
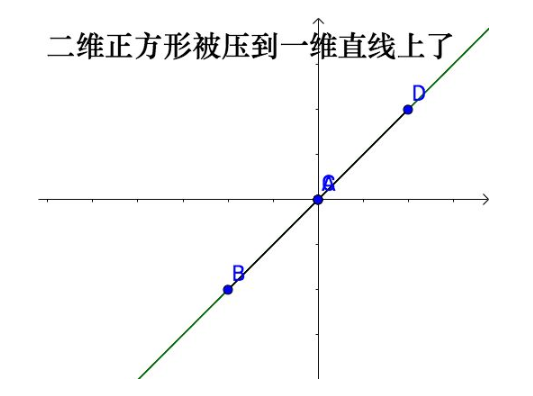
对于矩阵 [ 1 − 1 1 − 1 ] \begin{gathered} \begin{bmatrix} 1 & -1 \\ 1 & -1 \end{bmatrix} \end{gathered} [11−1−1],他的列空间是一维的
因此,这个矩阵的秩就是1,用它对二维的正方形进行线性变换,实际上是一个二维空间到另外一个一维空间的变换:
同理,矩阵 [ 0 0 0 0 ] \begin{gathered} \begin{bmatrix} 0 &0 \\ 0 & 0\end{bmatrix} \end{gathered} [0000]的列空间是个点,因此它的「秩」就是0。
这里来自知乎:什么是矩阵的秩
3.1 基础矩阵F(对极几何的代数表达式)
- 基础矩阵可以用来:
1)简化匹配
2)去除错匹配特征 - 基础矩阵描述了空间中的点在2个像平面中的坐标对应关系
x ′ T F x = 0 \mathbf{x’}^\mathrm{T}Fx=0 x′TFx=0
- 什么是双目立体视觉(Binocular Stereo Vision):是机器视觉的一种重要形式,它是基于视差原理并利用成像设备从不同的位置获取被测物体的两幅图像,通过计算图像对应点间的位置偏差,来获取物体三维几何信息的方法。
基础矩阵F的应用
- 立体视觉几何中有以下问题:
1)已知一幅图像中一点,如何寻找另一幅图像中这个点的对应点(可用光流法、特征点匹配法)
2)已知两幅图像中两点是对应关系,如何求解两相机的相对位置和姿态【R|t】
3)已知多幅图像中同一3D点的对应点,如何求解该3D点的3D坐标
对极几何/基础矩阵 的出现可以解决问题2。即求出R|t. - 给定一对同一场景不同视角得到的图像,对于第一幅图像上的任一像点x,在第二幅图像中都有一条与之对应的对极线l′,该对极线是像点x与过第一个相机中心C射线在第二幅图像上的投影,第二幅图像中与x相匹配的像点x′必定在该对极线上。因此,存在一个像点x到另一个图像上对极线l′的映射:x→l′
基础矩阵F表示的就是这种从点到直线的映射。 - 基础矩阵F的性质:
1)3*3且自由度为7的矩阵
2)F矩阵的秩为2
3)基本矩阵依赖内部和外部参数(Intrinsic and Extrinsic Parameters) (f, R & T)决定。
4)使用像素坐标系 - 自己对基本矩阵的理解:基本矩阵是很有用的一个工具,在三维重建和特征匹配上都可以用到。基本矩阵提供了三维点到二维的一个约束条件。举个例子,现在假设我们不知道空间点X的位置,只知道X在左边图上的投影x的坐标位置,也知道基本矩阵,首先我们知道的是X一定在射线Cx上,到底在哪一点是没法知道的,也就是X可能是Cx上的任意一点(也就是轨迹的意思),那么X在右图上的投影肯定也是一条直线。也就是说,如果我们知道一幅图像中的某一点和两幅图的基本矩阵,那么就能知道其对应的右图上的点一定是在一条直线上,这样就约束了两视角下的图像中的空间位置一定是有约束的,不是任意的。
- 于是VSLAM中相机的相对位姿可以通过特征点匹配估计出来:
1)提取两幅图像的特征点,并进行匹配
2)利用匹配得像点计算两视图的基础矩阵F
3 )从基础矩阵F中分解得到相机的旋转矩阵R和平移向量t
3.2 本质矩阵E
- 本质矩阵描述了空间中的点在两个坐标系中坐标对应关系
p ′ T E p = 0 \mathbf{p’}^\mathrm{T}Ep=0 p′TEp=0
- 本质矩阵E:E矩阵同样表示的是对极约束的关系,但它不再涉及相机内参,只由两视图之间的姿态关系决定。
1)描述空间中一点在不同帧之间的几何约束关系
2)注意这里的图像坐标是空间点在相机平面投影点的齐次坐标(摄像机坐标系下表示)
3)本质矩阵和相机外参有关系,和内参无关 - 本质矩阵E的性质:
1)3*3且自由度为5的矩阵
2)因为只包含R,t共有6个自由度,又因为尺度等价去掉一个自由度
3)本质矩阵E的奇异值必定为 [ σ , σ , 0 ] T [\sigma ,\sigma ,0]^{T} [σ,σ,0]T的形式
4)本质矩阵的秩为2
5)本质矩阵仅依赖外部参数(Extrinsic Parameters) (R & T)决定。
6) 使用摄像机(Camera)坐标系 - 自己对本质矩阵的理解:为了获取本质矩阵,首先计算基础矩阵F。(本质矩阵是基础矩阵的一个子集,不知道这样理解对不对?)根据本质矩阵E,就可恢复得到运动的状态R和T。
4. 八点算法估计基础矩阵F
- 基本矩阵的方程定义:
x ′ − T F x = 0 \mathbf{x’}^\mathrm{-T}F_x=0 x′
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/120682.html