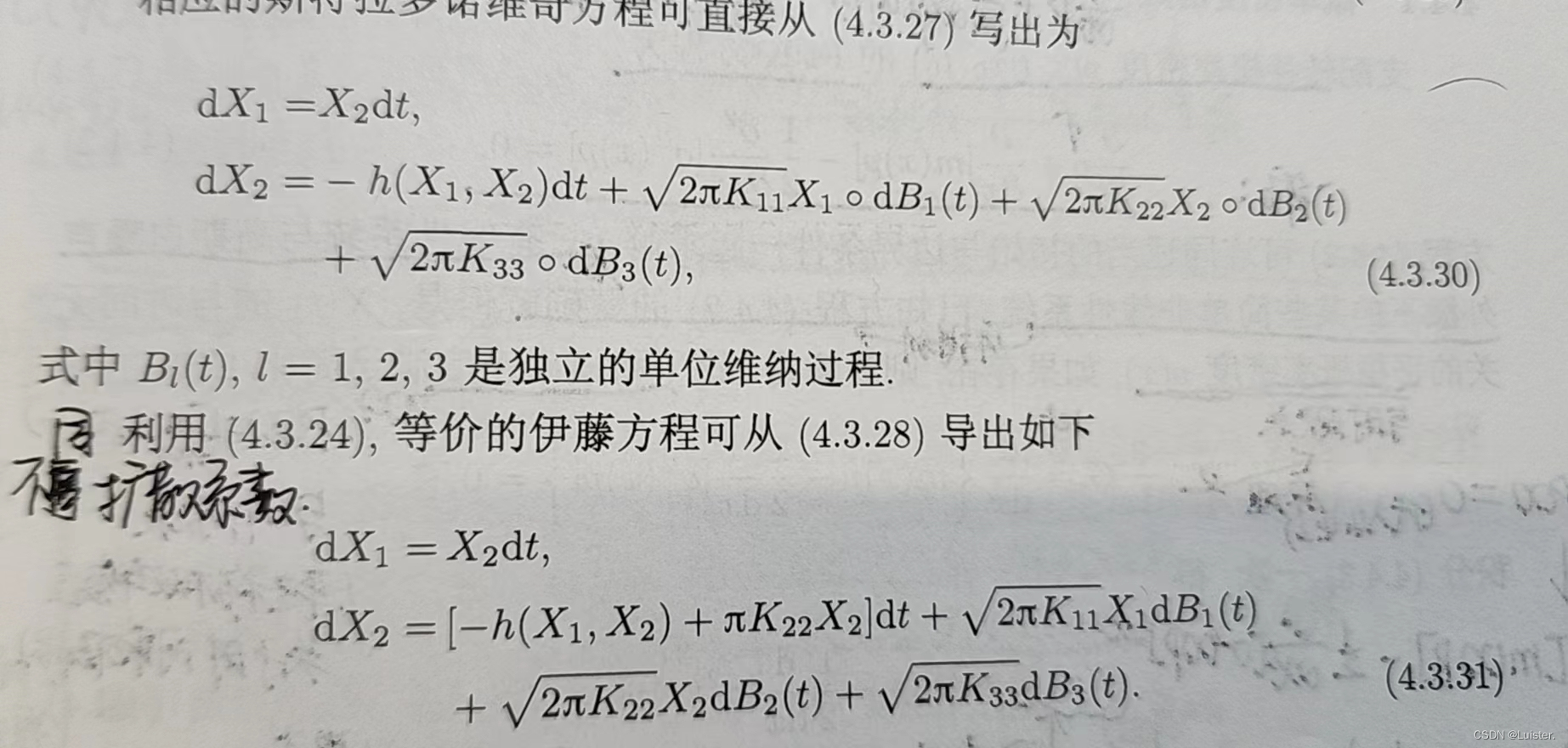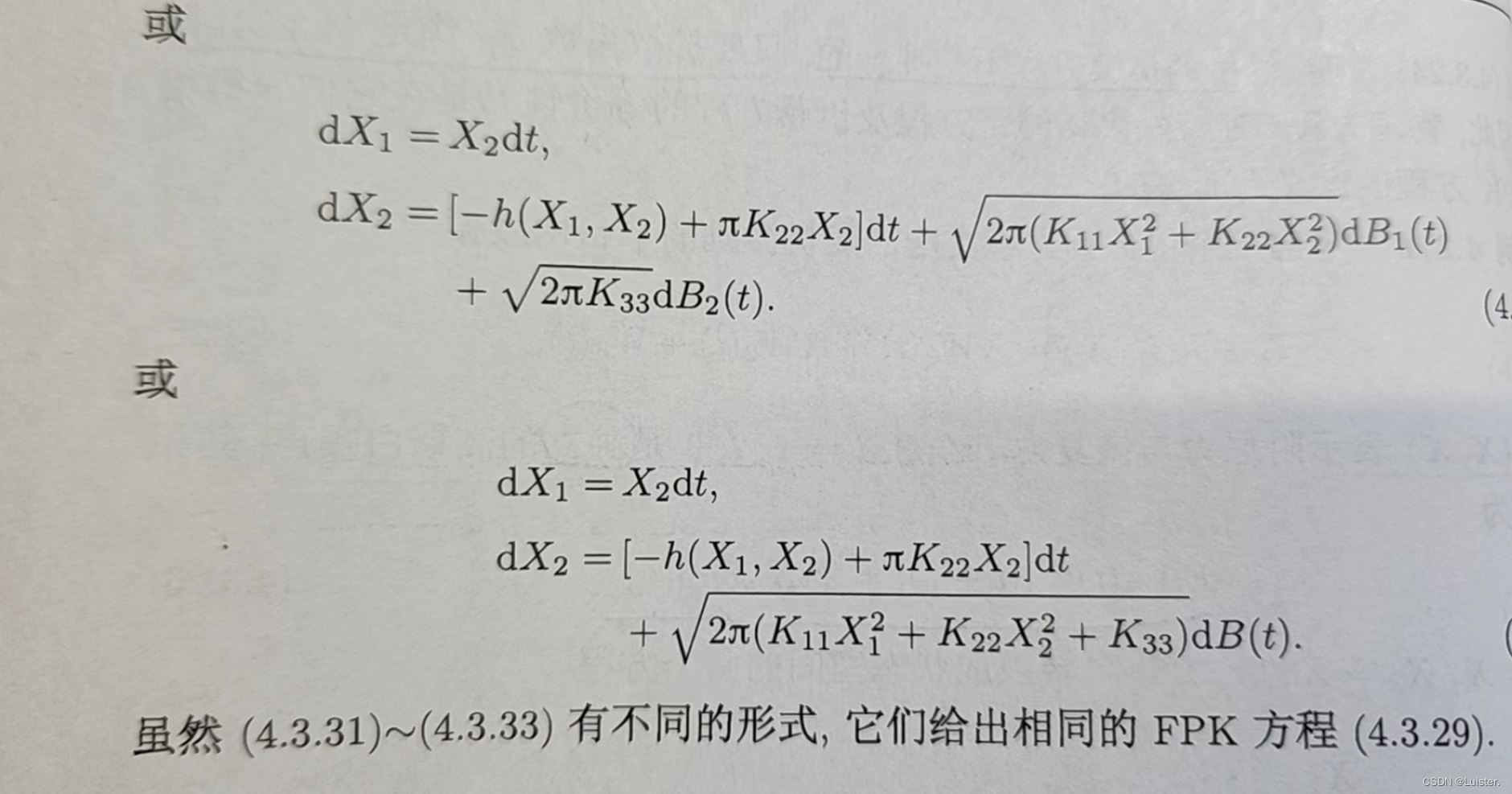简单随机微分方程数值解

大家好，欢迎来到IT知识分享网。

1.随机微分方程求解：dX(t) =− αXtdt + σdWt

%% %O-U过程 %dX(t)=-alpha*Xt*dt+sigma*dWt,X|t=0=X0 %alpha=2,sigma=1,X0=1 % 设置初始参数 T = 1; % 时间区间长度 N = 1000; % 离散化的时间步数 dt = T/N; % 时间步长 X = zeros(1,N+1); % 存储解向量 X(1) = 1; % 初始条件 alpha = 2; sigma = 1; % 模拟数值解 for i = 1:N dW = sqrt(dt)*randn(); % 标准正态分布增量 X(i+1) = X(i) - alpha*X(i)*dt + sigma*dW; % 欧拉方法更新 end % 绘图 plot(linspace(0,T,N+1),X,'*-') % 根据时间步长将x轴离散化 xlabel('t') ylabel('X(t)') title('随机微分方程数值解') legend('Euler数值解') 

法二：Milstein

% 设置参数 alpha = 2; sigma = 1; X0 = 1; T = 1; N = 1000; dt = T/N; % 初始化向量和随机项 t = 0:dt:T; W = [0,cumsum(randn(1,N).*sqrt(dt))]; %使用cumsum函数生成一个与t等长的Wiener过程（随机项） % 初始化X X = zeros(1,N+1); X(1) = X0; % Milstein方法计算X for i = 1:N dW = W(i+1) - W(i); X(i+1) = X(i) - alpha*X(i)*dt + sigma*X(i)*dW ... + 0.5*sigma^2*X(i)*(dW^2-dt); %在Milstein方法中，我们需要对二次变差数进行估计 %因此在计算时需要添加正交项0.5*sigma^2*X(i)*(dW^2-dt) end % 绘制图形 plot(t,X,'*-') title('随机微分方程数值解') xlabel('t') ylabel('X(t)') legend('Milstein数值解') 

2.受高斯白噪声激励的系统，FPK求解

记$X_1=X,X_2=\dot{X}$可转换状态空间的两个方程
${\dot{X}}_1=X_2$
${\dot{X}}_2=-h(X_1,X_2)+X_1{W}_1(t)+X_2{W}_2(t)+W_3(t)$

对于$\frac{d}{dt}X(t)=f(X,t)+g(X,t)W(t)$
相应的FPK方程为$\frac{\partial }{\partial t}p+{\sum }_{j=1}^n\frac{\partial }{\partial x_j}(a_{j}p)-\frac{1}{2}{\sum }_{j,k=1}^n\frac{{\partial }^2}{\partial x_j\partial x_k}(b_{jk}p)=0$
其中，一、二阶导数矩为$a_j(\mathbf{x},t)=f_j(\mathbf{x},t)+\pi {\sum }_{r=1}^n{\sum }_{l,s=1}^m{K}_{ls}{g}_{rs}(\mathbf{x},t)\frac{\partial }{\partial x_r}{g}_{jl}(\mathbf{x},t)$,
$b_{jk}(\mathbf{x},t)=2\pi {\sum }_{l,s=1}^m{K}_{ls}{g}_{jl}(\mathbf{x},t)g_{ks}(\mathbf{x},t)$

由此可以得出,$f_1=x_2,f_2=-h(x_1,x_2)$,$g_{1j}=0(j=1,2,3)$
$g_{21}=x_1,g_{22}=x_2,g_{23}=1$,$n=2,m=3$.
则一、二阶导数矩：
$a_1=x_2,a_2=-h(x_1,x_2)+\pi K_{22}{x}_2$
$b_{11}=0,b_{12}=0,b_{21}=0.b_{22}=2\pi K_{11}{x}_1^2+2\pi K_{22}{x}_2^2+2\pi K_{33}.$
从而得到FPK方程：
∂ ∂ t p + ∂ ∂ x 1 ( x 2 p ) + ∂ ∂ x 2 { [ ( − h ( x 1 , x 2 + π K 22 x 2 ] p } − π ∂ 2 ∂ x 2 2 [ ( K 11 x 1 2 + K 22 x 2 2 + K 33 ) p ] = 0 \frac{\partial}{\partial t}p+\frac{\partial}{\partial x_{1}}(x_{2}p)+\frac{\partial}{\partial x_{2}}\left \{ [(-h(x_{1},x_{2}+\pi K_{22}x_{2}]p \right \}-\pi \frac{\partial ^{2}}{\partial x_{2}^{2}}[(K_{11}x_{1}^{2}+K_{22}x_{2}^{2}+K_{33})p]=0 ∂t∂​p+∂x1​∂​(x2​p)+∂x2​∂​{
[(−h(x1​,x2​+πK22​x2​]p}−π∂x22​∂2​[(K11​x12​+K22​x22​+K33​)p]=0.

相应的也可以得到Stratonovich或Ito方程，它们得到的FPK方程都和上式一致。

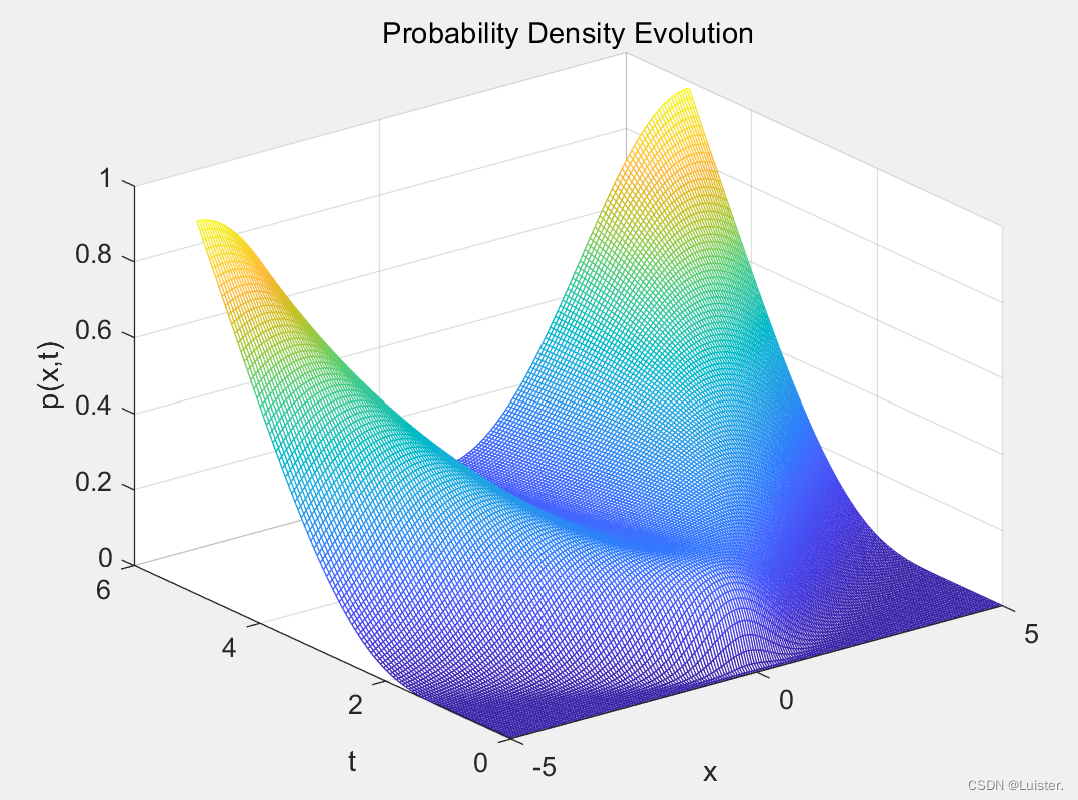
3.绘制随机微分方程概率密度曲线

%(b) clc;clear; % 定义需要绘制的变量和参数 t_values = linspace(0.01, 5, 100); % 在t轴上均匀采样100个点，保证不会出现除数为0的情况 x_values = linspace(-5, 5, 200); % 在x轴上均匀采样200个点 [x_mesh, t_mesh] = meshgrid(x_values, t_values); % 创建网格 % 计算概率密度函数 p = (1./sqrt(2*pi.*t_mesh)).*cosh(x_mesh).*exp(-0.5./t_mesh).*exp(-(x_mesh.^2)./(2*t_mesh)); % 绘制演化图 mesh(x_mesh, t_mesh, p); % 使用surf函数绘制三维曲面图 xlabel('x'); ylabel('t'); zlabel('p(x,t)'); % 添加轴标签 title('Probability Density Evolution'); % 添加标题 

fortran中设置感兴趣区间[-5,5],时间间隔0.01，分胞数50,跑1万条轨迹，每个迭代500次后得到如下结果：