坐标变换（二维、三维）

大家好，欢迎来到IT知识分享网。

一、四种空间

1.1 定义和对比

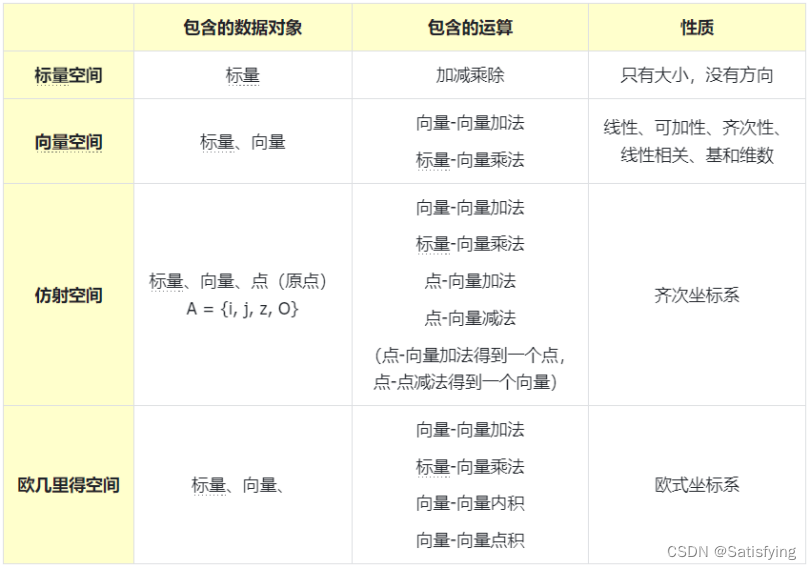
• 标量空间：只有标量；
• 向量空间（Vector space）：除了标量，还有向量；
• 仿射空间（Affine space）：除了标量、向量，还有点。向量空间没有位置的概念，所以不能表述几何物体，因此需要用到仿射空间；（对应齐次坐标系）
• 欧几里得空间（Euclidean space）：除了标量、向量，还有距离。仿射空间定义了点，包含了构建几何模型的必要元素，但是仿射空间没有定义长度的概念，欧几里得空间引入了这个概念。（对应欧几里得坐标系）
  
  

1.2 齐次坐标系

若在三维空间中有一个向量表示为$v=(a,b,c)$，即$v=ai+bj+cz$，那么表示为在三维仿射空间中的一个数学对象$object=ai+bj+cz+dO$。当 d=0 时，object 就是一个向量；当 d≠0 时，object 就是一个向量加上一个点，也就是一个点。因此，在齐次坐标系下，既可以表示向量，又可以表示点。在齐次坐标系中，向量的坐标形式为$v=(x,y,z,0)$用以表示$v=ai+bj+cz$；点的坐标形式为$P=(a,b,c,d)$用以表示$v=(a/d)i+(b/d)j+(c/d)z+O$。也就是说，在三维空间中可以认为$(x,y,z)$是点，也可以认为是向量，

齐次坐标：使用 N+1 维坐标来表示 N 维坐标。齐次坐标具有规模不变性，同一点可以被无数个齐次坐标表达$(X,Y,1)\to (ax,ay,a)$齐次坐标转化为笛卡尔坐标可以通过同除最后一项得到。在计算机图形学中，为了统一将平移、旋转、缩放等用矩阵表示，需要引入齐次坐标。比如使用$2\ast 2$的矩阵没有办法描述平移操作，需要引入$3\ast 3$的矩阵，才能统一描述二维中的平移、旋转、缩放等操作。同理，必须使用$4\ast 4$的矩阵才能描述三维变换。

二、刚性变换

2.1 定义

只有平移和旋转，物体的形状不发生改变的变换。

2.2 平移

2.3 旋转

二维旋转是围绕一个点进行旋转，三维旋转是围绕一个轴进行旋转。

一文读懂图像中点的坐标变换(刚体变换，相似变换，仿射变换，投影变换)

Python 3D坐标系下的点的转换矩阵（平移、缩放、旋转、错切）

2.3.1 二维

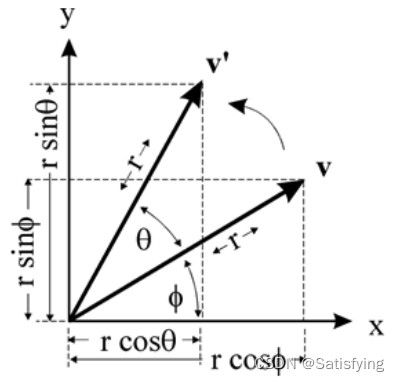
2.3.1.1 绕原点

2.3.1.2 绕任意点

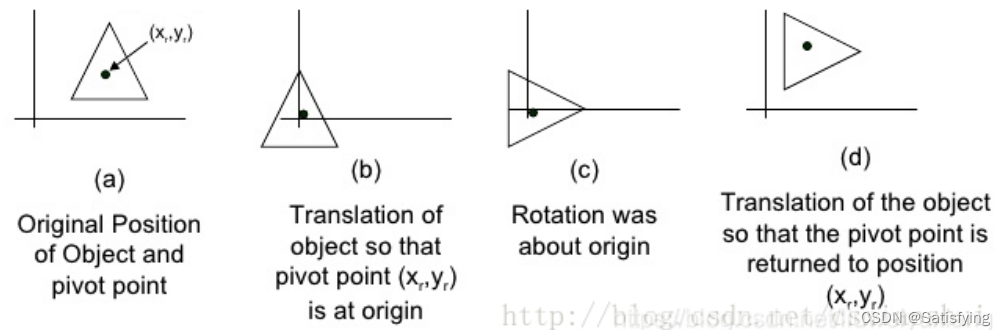
绕任意点旋转可以转换为绕原点的旋转，处理思路：①首先将旋转点移动到原点处；②执行绕原点旋转；③再将旋转点移回到原来位置。也就是说，绕任意点的旋转可以处理为：平移+绕原点旋转+平移。因此，绕任意点旋转的旋转矩阵为：
$$\begin{array}{rl}M& =\left[\begin{array}{c}10t_x\\ 01t_y\\ 001\end{array}\right]\left[\begin{array}{c}cos\theta -sin\theta 0\\ sin\theta cos\theta 0\\ 001\end{array}\right]\left[\begin{array}{c}10-t_x\\ 01-t_y\\ 001\end{array}\right]\\ & \\ & =\left[\begin{array}{c}cos\theta -sin\theta (1-cos\theta )t_x+t_{y}sin\theta \\ sin\theta cos\theta (1-cos\theta )t_y-t_{x}sin\theta \\ 001\end{array}\right]\end{array}$$

2.3.2 三维

3维旋转矩阵推导与助记

2.3.2.1 绕x轴

2.3.2.2 绕y轴

2.3.2.3 绕z轴