一阶电路基础知识_IT分享知识网

大家好，欢迎来到IT知识分享网。

什么是一阶电路

一阶电路（First-order circuit）是指由一个电感（L）或一个电容（C）和一个电阻（R）组成的电路。

根据电感或电容的位置，一阶电路可以分为RC电路、RL电路、LC电路、RLC电路。

一阶电路常用于滤波、放大、时序控制等各种电子设备和系统中。通过调整电阻、电容或电感的数值，可以改变电路的频率响应、滞后/提前相位等特性，实现不同的功能和性能

一阶、二阶电路区别

一阶电路由一个电容或一个电感与一个电阻组成，而二阶电路则由两个电容或两个电感与一个电阻组成。二阶电路相比于一阶电路具有更多的元件和参数，因此结构上更为复杂。这种结构差异导致了一阶电路和二阶电路在频率响应和时域特性上的差异。

N 阶电路

几阶便是电源电路中几个储能技术元器件，电容器或是电感器，一个便是一阶，一个电容器加一个电感器便是二阶，2个电容器也是二阶。注意：两个电容并联和两个电容串联算一阶

RC/CR串并联电路截止频率

不管是高通还是低通滤波器其截止频率（转折频率）计算公式都为：f=1/(2πRC)

随着频率的增大，电容的阻抗趋近于0，而此时的信号频率称为转折频率f0；

RC/CR串联电路阻抗特性曲线

计算截止频率

举一个具体的例子。电阻1000Ω电容1uf，计算出的截止频率为159.2HZ。也就是说，在高通滤波的情况下，159.2HZ频率以下的信号都会被滤掉，在低通滤波的情况下159.2HZ以上的频率都会被滤掉。

CR串联电路

又叫高通滤波器=微分电路=超前移相电路

高通滤波器的工作原理：

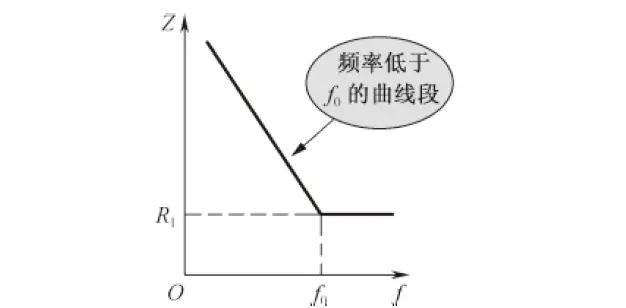
当输入信号频率𝑓<𝑓0 时，由于C1的容抗很大而受到阻止，输出减小，且频率愈低输出愈小。在频率为零（直流电）时，该电路的阻抗为无穷大，因为电容C对直流电呈开路状态。

在输入信号频率f ＞𝑓0 时，整个 RC 串联电路总的阻抗基本不变了，其大小等于 R1，由于C1容抗已很小，故对信号无衰减作用，这样该滤波器具有让高频信号通过，阻止低频信号的作用。

微分电路波形

当输入电压为阶跃变化的矩形脉冲时，且RC电路的充放电时间常数τ=RC＜TK(脉冲宽度)时,能将输入的矩形脉冲变成宽度为τ的尖脉冲。

超前移相电路

不同频率的正弦信号通过RC电路时,电路所反映出的性质。信号频率越低，输出电压相对于输入电压的超前就越大。当信号频率等于截止频率，即ωRC=1时，输出电压比输入电压超前45º。ωRC→0时，超前移相可达90º。

RC串联电路

又叫低通滤波器=积分电路=滞后移相电路=缓冲电路

RC低通滤波器的工作原理：

当输入信号频率𝑓<𝑓0 时，由于C1容抗已很小，故对信号无衰减作用，这样该滤波器具有让低频信号通过，阻止高频信号的作用。

在输入信号频率f ＞𝑓0 时，由于C1容抗很大，故对信号有衰减作用，阻止高频信号。

积分电路波形

当输入电压为阶跃变化的矩形脉冲时， RC电路的时常数τ=RC＞TK(脉冲宽度)时,能将输入的矩形脉冲变成幅度随时间线性变化的锯齿波。

滞后移相电路

不同频率的正弦信号通过RC电路时,电路所反映出的性质。信号频率越高，输出电压相对于输入电压的滞后就越大。当信号频率等于截止频率，即ωRC=1时，输出电压比输入电压滞后45º。ωRC→∞时，滞后移相可达90º。

RC并联电路

RC 并联电路既可通过直流又可通过交流信号。故可以是低通滤波器，也可是高通滤波器。

RC并联电路如果串联在电路中有衰减低频信号的作用，也就是滤波的作用。

它和RC串联电路有着同样的转折频率：f0=1/（2πR1C1）。

RC 并联电路

RC 并联电路阻抗特性曲线

在输入信号频率f ＞𝑓0 后， C1 的容抗相对很小，由于C1 与R1 并联，总阻抗为电阻阻值并上电容容抗，其总的阻抗下降。当频率高到一定程度后，总的阻抗为0。

当输入信号频率𝑓<𝑓0 时，信号相对电路为直流，由于电容C1 的容抗很大（与R1 相比很大）而相当于开路，此时整个电路的总阻抗等于R1。

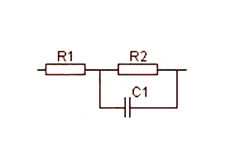
RC串并联电路

RC 串并联电路存在两个转折频率f01 和 f02:

　　f01=1/2πR2C1, f02=1/2πC1*[R1*R2/(R1+R2)]

　　当信号频率低于 f01 时，C1 相当于开路，该电路总阻抗为 R1+R2。

　　当信号频率高于 f02 时，C1 相当于短路，此时电路总阻抗为 R1。

　　当信号频率高于 f01 低于 f02 时，该电路总阻抗在 R1+R2 到R1之间变化。

RC串联接地电路

基本的RC吸收电路，主要是为了解决MOSFET开关的尖峰问题

电阻R 的最重要作用是产生阻尼，吸收电压尖峰的谐振能量，是功率器件。

电容C的作用并不是电压吸收，而是为R阻尼提供能量通道。

RC吸收并联MOS管上，C提供能量通道，C 的大小决定吸收程度，最终目的是使R形成功率吸收。

RL/LR串并联电路截止频率

不管是高通还是低通滤波器其截止频率（转折频率）计算公式都为:

RL串联电路阻抗特性曲线

LR串联电路

又叫低通滤波器=积分电路=滞后移相电路

滞后移相电路

电感器上的电压滞后电流 90°

当输入信号频率𝑓<𝑓0 时，低频信号无损通过，感抗为0，总阻抗为R，但信号不经过电阻R，直接到Vo。

在输入信号频率f ＞𝑓0 后，由于L感抗很大，故对信号有衰减作用，阻止高频信号。

积分电路波形

RL串联电路

又叫高通滤波器=微分电路=超前移相电路

超前移相电路

电感器上的电压超前电流 90°

当输入信号频率𝑓＜𝑓0 时，信号幅值无损通过R和L，信号不经过Vo，感抗低频为0，总阻抗是R，

当输入信号频率𝑓＞𝑓0 时，由于L感抗很大，故信号不经过电感L，直接从R到Vo，这样具有让高频信号通过，阻止低频信号的作用。

微分电路波形

RL并联电路

RL并联电路如果串联在电路中有衰减高频信号的作用，也就是滤波的作用。

它和RL串联电路有着同样的转折频率：f0=R /（2πL）。

RL并联电路既可通过直流又可通过交流信号。故可以是低通滤波器，也可是高通滤波器。

当输入信号频率𝑓＜𝑓0 时，直流信号通过R或L，总阻抗是R；当输入信号频率𝑓＞𝑓0 时，L感抗很大，信号不经过电感L，只经过R，总阻抗很大。

LC/CL串并联电路截止频率

在谐振时，并联电路产生与串联谐振电路相同的方程。因此，电感或电容是并联还是串联没有区别。

对于 LC 谐振电路来说，当外部输入信号的频率等于其自身的谐振频率时，LC 电路中的容抗和感抗相等，即 XL = XC, 因此，我们使用数学符号表达 LC 谐振电路如下：

串联谐振电路特点

● 总阻抗值最小

● 电源电压一定时，电流最大

● 电路呈电阻性，电容或电感上的电压可能高于电源电压

并联谐振电路的特点

● 电压一定时，谐振时电流最小

● 总阻抗最大

● 电路呈电阻性，支路电流可能会大于总电流

LC串联电路

又叫谐振电路、振荡电路、低通滤波器、积分电路

LC 串联谐振电路阻抗特性曲线

输入信号频率等于谐振频率f0 时阻抗特性曲线

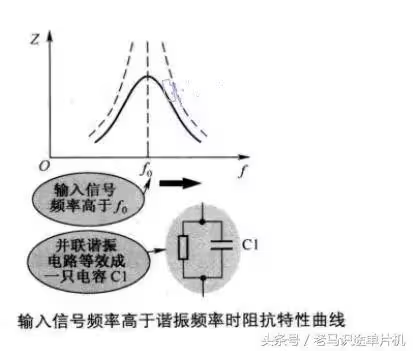
输入信号频率高于谐振频率f0 时阻抗特性曲线

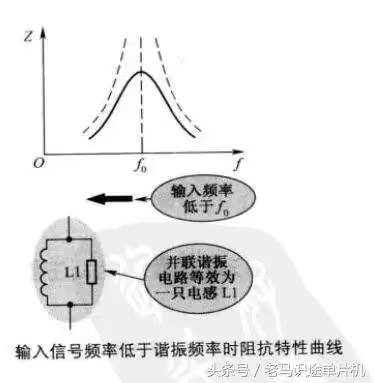
输入信号频率低于谐振频率f0 时阻抗特性曲线

低通滤波器电感特性阻抗曲线

CL串联电路

又叫谐振电路、振荡电路、高通滤波器、积分电路

高通滤波器电容特性阻抗曲线

LC并联电路

又叫谐振电路、振荡电路、带阻电路

① 输入信号频率等于谐振频率时阻抗特性曲线：

在谐振时，并联LC谐振电路就像一个开路，当在这种状态下总电流最小时，则总阻抗最大。因此，谐振时并联谐振电路的总阻抗变为电路中的电阻值，并且Z= R ,如下图所示。

③ 输入信号频率低于谐振频率时阻抗特性曲线：

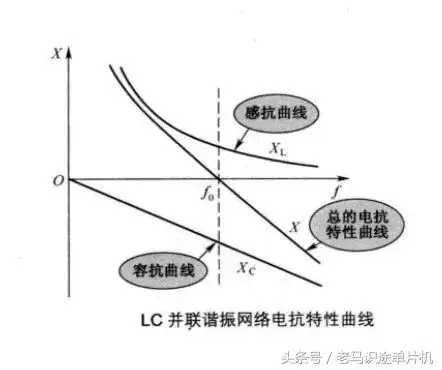
④ LC并联谐振网络电抗特性曲线：

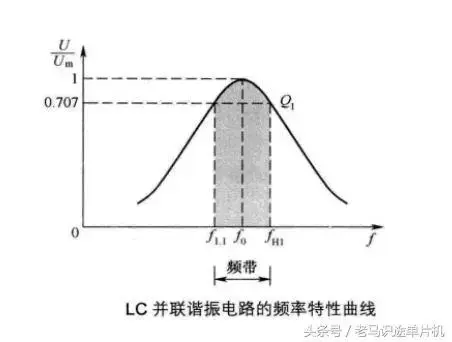
⑤ LC并联谐振电路电路的频率特性曲线：

RLC串联电路