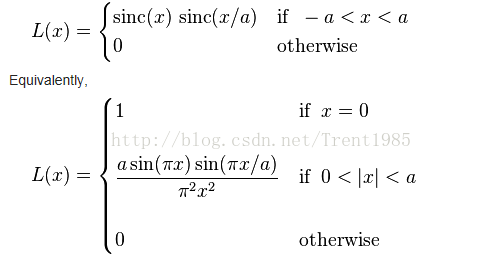大家好,欢迎来到IT知识分享网。
[研究内容]
目前比较常用的几种插值算法
[正文]
目前比较常用的插值算法有这么几种:最邻近插值,双线性二次插值,三次插值,
Lanczos插值等等,今天我们来对比一下这几种插值效果的优劣。
1,最邻近插值
最邻近插值算法也叫做零阶插值算法,主要原理是让输出像素的像素值等于邻域内离它距离最近的像素值。例如下图中所示,P1距离0灰度值像素的距离小于100灰度值的距离,因此,P1位置的插值像素为0。这个算法的优点是计算简单方便,缺点是图像容易出现锯齿。
2,双线性二次插值
f ( i , j + 1 ) f(i,j+1) f(i,j+1)和 f ( i + 1 , j + 1 ) f(i+1,j+1) f(i+1,j+1)求取 f ( x , j + 1 ) f(x,j+1) f(x,j+1),然后再根据这两点的二次插值求取 f ( x , y ) f(x,y) f(x,y)。
根据前面的例题,我们可以很容易的求取各点插值如下:
(1-4) f ( x , j ) = ( i + 1 − x ) f ( i , j ) + ( x − i ) f ( i + 1 , j ) f(x,j)=(i+1-x)f(i,j)+(x-i)f(i+1,j) \tag{1-4} f(x,j)=(i+1−x)f(i,j)+(x−i)f(i+1,j)(1–4)
(1-5) f ( x , j + 1 ) = ( i + 1 − x ) f ( i , j + 1 ) + ( x − i ) f ( i + 1 , j + 1 ) f(x,j+1)=(i+1-x)f(i,j+1)+(x-i)f(i+1,j+1) \tag{1-5} f(x,j+1)=(i+1−x)f(i,j+1)+(x−i)f(i+1,j+1)(1–5)
(1-6) f ( x , y ) = ( i + 1 − y ) f ( x , j ) + ( y − j ) f ( x , j + 1 ) f(x,y)=(i+1-y)f(x,j)+(y-j)f(x,j+1) \tag{1-6} f(x,y)=(i+1−y)f(x,j)+(y−j)f(x,j+1)(1–6)
以上三式综合可以得到:
(1-7) f ( x , y ) = ( j + 1 − y ) ( i + 1 − x ) f ( i , j ) + ( j + 1 − y ) ( x − i ) f ( i + 1 , j ) + ( y − j ) ( i + 1 − x ) f ( i , j + 1 ) + ( y − j ) ( x − i ) f ( i + 1 , j + 1 ) \begin{aligned} f(x,y)=&(j+1-y)(i+1-x)f(i,j)+(j+1-y)(x-i)f(i+1,j)\\&+(y-j)(i+1-x)f(i,j+1)+(y-j)(x-i)f(i+1,j+1) \tag{1-7} \end{aligned} f(x,y)=(j+1−y)(i+1−x)f(i,j)+(j+1−y)(x−i)f(i+1,j)+(y−j)(i+1−x)f(i,j+1)+(y−j)(x−i)f(i+1,j+1)(1–7)
我们令 x = i + p , y = j + q x=i+p,y=j+q x=i+p,y=j+q得:
(1-8) f ( i + p , j + q ) = ( 1 − q ) ( 1 − p ) f ( I , j ) + p ( 1 − q ) f ( i + 1 , j ) + q ( 1 − p ) f ( i , j + 1 ) + p q f ( i + 1 , j + 1 ) \begin{aligned} f(i+p,j+q)=&(1-q)(1-p)f(I,j)+p(1-q)f(i+1,j)+q(1-p)f(i,j+1)\\ &+pqf(i+1,j+1) \tag{1-8} \end{aligned} f(i+p,j+q)=(1−q)(1−p)f(I,j)+p(1−q)f(i+1,j)+q(1−p)f(i,j+1)+pqf(i+1,j+1)(1–8)
上式即为数字图像处理中的双线性二次插值公式。
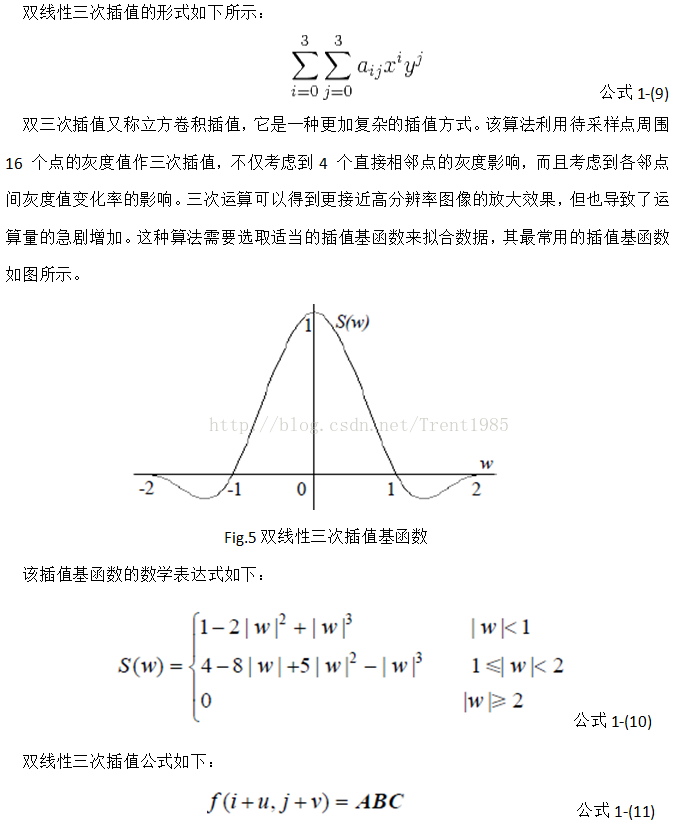
3,双线性三次插值
(1-12) A = [ S ( 1 + v ) S ( v ) S ( 1 − v ) S ( 2 − v ) ] A= \begin{bmatrix} S(1+v)&S(v)&S(1-v)&S(2-v) \end{bmatrix} \tag{1-12} A=[S(1+v)S(v)S(1−v)S(2−v)](1–12)
(1-13) B = [ f ( i − 1 , j − 1 ) f ( i − 1 , j ) f ( i − 1 , j + 1 ) f ( i − 1 , j + 2 ) f ( i , j − 1 ) f ( i , j ) f ( i , j + 1 ) f ( i , j + 2 ) f ( i + 1 , j − 1 ) f ( i + 1 , j ) f ( i + 1 , j + 1 ) f ( i + 1 , j + 2 ) f ( i + 2 , j − 1 ) f ( i + 2 , j ) f ( i + 2 , j + 1 ) f ( i + 2 , j + 2 ) ] B= \begin{bmatrix} f(i-1,j-1)&f(i-1,j)&f(i-1,j+1)&f(i-1,j+2)\\ f(i,j-1)&f(i,j)&f(i,j+1)&f(i,j+2)\\ f(i+1,j-1)&f(i+1,j)&f(i+1,j+1)&f(i+1,j+2)\\ f(i+2,j-1)&f(i+2,j)&f(i+2,j+1)&f(i+2,j+2) \end{bmatrix} \tag{1-13} B=⎣⎢⎢⎡f(i−1,j−1)f(i,j−1)f(i+1,j−1)f(i+2,j−1)f(i−1,j)f(i,j)f(i+1,j)f(i+2,j)f(i−1,j+1)f(i,j+1)f(i+1,j+1)f(i+2,j+1)f(i−1,j+2)f(i,j+2)f(i+1,j+2)f(i+2,j+2)⎦⎥⎥⎤(1–13)
(1-14) C = [ S ( 1 + u ) S ( u ) S ( 1 − u ) S ( 2 − u ) ] C= \begin{bmatrix} S(1+u)\\ S(u)\\ S(1-u)\\ S(2-u) \end{bmatrix} \tag{1-14} C=⎣⎢⎢⎡S(1+u)S(u)S(1−u)S(2−u)⎦⎥⎥⎤(1–14)
等价于(可自行推导)
(1-15) f ( i + v , j + u ) = ∑ r o w = − 1 2 ∑ c o l = − 1 2 f ( i + r o w , j + c o l ) S ( r o w − v ) S ( c o l − u ) f(i+v,j+u)=\sum_{row=-1}^{2}\sum_{col=-1}^{2}f(i+row,j+col)S(row-v)S(col-u) \tag{1-15} f(i+v,j+u)=row=−1∑2col=−1∑2f(i+row,j+col)S(row−v)S(col−u)(1–15)
提示:
一定要区分本文中 v v v, u u u和 r o w row row, c o l col col的对应关系, v v v代表行数偏差, u u u代表列数偏差(如果混淆了,会造成最终的图像偏差很大)
4,Lanczos插值算法
该算法的主要原理介绍地址:http://en.wikipedia.org/wiki/Lanczos_resampling
这里我大概介绍一下算法的流程:
这个算法也是一个模板算法,主要内容是计算模板中的权重信息。
对于一维信息,假如我们输入点集为 X X X,那么,Lanczos对应有个窗口模板Window,这个窗口中每个位置的权重计算如下:
Fig.6 Lanczos
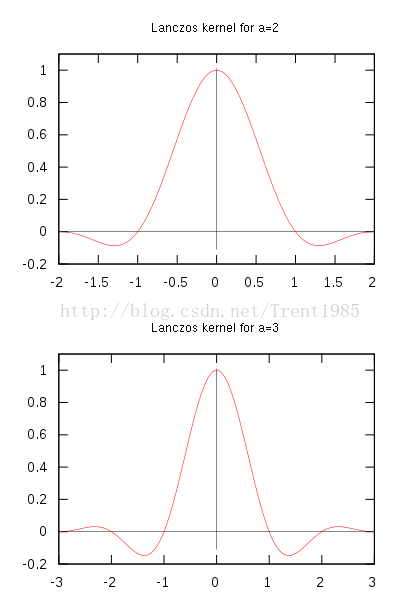
通常,这个 a a a取2或者3, a = 2 a=2 a=2时,该算法适用于图像缩小插值; a = 3 a=3 a=3时,该算法适用于放大插值;对应不同 a a a值得Lanczos插值曲线如上图6所示;上述的公式分别为连续和离散的公式。我们根据输入点X的位置,确定对应window中不同位置的权重L(x),然后对模板中的点值取加权平均,公式如下:
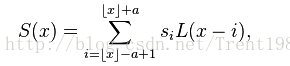
这个 S ( x ) S(x) S(x)即为 X X X处的插值结果。
由于编程语言不同,可能会造成耗时的差距,但是,对于同一种语言,统计得出:最邻近插值速度最快,三次插值速度最慢,而Lanczos算法与二次插值相仿。
综上,Lanczos插值具有速度快,效果好,性价比最高的优点,这也是目前此算法比较流行的原因。
转载自:Lanczos插值,最邻近插值,双线性二次插值,三次插值
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/122676.html