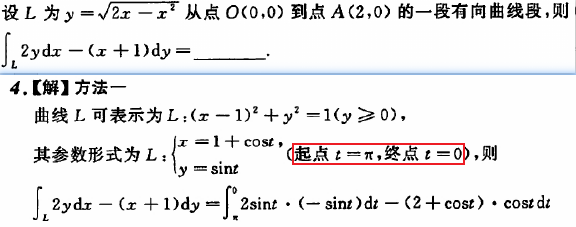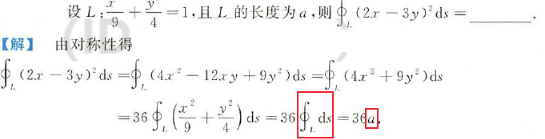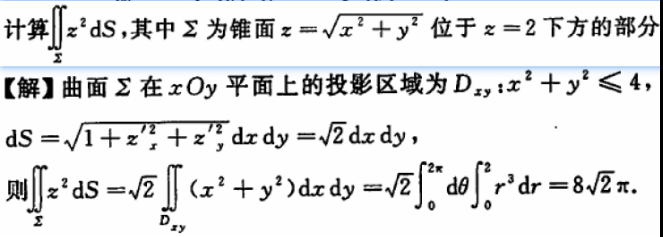大家好,欢迎来到IT知识分享网。
文章目录
一 曲线积分
1.1 第一类(弧长)
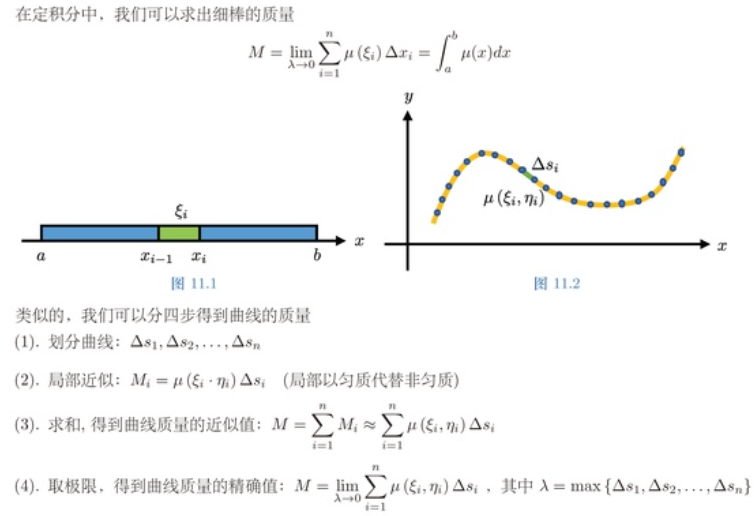
背景
曲线的质量
概念与性质
定义 小s表线
∫ L f ( x , y ) d s = lim λ → 0 ∑ i = 1 n f ( ξ i , η i ) Δ s i \int_{L} {f(x, y)} d s=\lim _{\lambda \rightarrow 0} \sum_{i=1}^n f\left(\xi_{i}, \eta_{i}\right) \Delta s_{i} ∫Lf(x,y)ds=λ→0limi=1∑nf(ξi,ηi)Δsi
意义(可知与方向无关)
数值上==有向柱面面积,但被积函数恒为1时,数值等于曲线长度
性质
线性
$ \int_{L}[{f(x, y)} \pm g(x, y)] d s=\int_{L} {f(x, y)} d s \pm \int_{L} g(x, y) d s $
$ \int_{L} k \cdot {f(x, y)} d s=k \int_{L} {f(x, y)} d s \quad(k 为常数 为常数 为常数 ) $
$ \int_{L_{1}+L_{2}} {f(x, y)} d s=\int_{L_{1}} {f(x, y)} d s+\int_{L_{2}} {f(x, y)} d s $
$ \int_{L} d s=s=L $的弧长
奇偶性
轮换对称性
计算方法
步骤:边界代入—对称性相加除以2—奇偶性得两倍或消除部分—直(极)坐标或参数方程。存在圆的方程时候考虑转化为参数方程
特殊代替
【例题】
定积分法
步骤:检查边界方程能否代入被积函数—奇偶性对称性—转换为恰当形式(直角坐标、参数方程 )
直接坐标法
∫ L f ( x , y ) d s = ∫ α β f [ x , y ( x ) ] 1 + y ′ ( x ) d x \int_{L} {f(x, y)} d s=\int_{\alpha}^{\beta} f[x, y(x)] \sqrt{1+y^{‘}(x)} d x ∫Lf(x,y)ds=∫αβf[x,y(x)]1+y′(x)dx
参数方程法
L 由极坐标给出: ρ = ρ ( θ ) , α ≤ θ ≤ β \rho=\rho(\theta), \alpha \leq \theta \leq \beta ρ=ρ(θ),α≤θ≤β ,则
∫ L f ( x , y ) d s = ∫ α β f [ ρ cos θ , ρ sin θ ] ρ 2 ( θ ) + ( ρ ′ ( θ ) ) 2 d θ \int_{L} {f(x, y)} d s=\int_{\alpha}^{\beta} f[\rho \cos \theta, \rho \sin \theta] \sqrt{\rho^2(\theta)+(\rho'(\theta))^2} d \theta ∫Lf(x,y)ds=∫αβf[ρcosθ,ρsinθ]ρ2(θ)+(ρ′(θ))2dθ
空间曲线下参数法
∫ L f ( x , y , z ) d s = ∫ α β f [ x ( t ) , y ( t ) , z ( t ) ] x ′ 2 ( t ) + y ′ 2 ( t ) + z ′ 2 ( t ) d t \int_{L} {f(x, y, z)} d s=\int_{\alpha}^{\beta} f[x(t), y(t), z(t)] \sqrt{x^{\prime2}(t)+y^{\prime2}(t)+z^{\prime2}(t)} d t ∫Lf(x,y,z)ds=∫αβf[x(t),y(t),z(t)]x′2(t)+y′2(t)+z′2(t)dt
直线化为参数方程的方法 880 例题6
圆的极坐标
【例题】2018数一
1.2 第二类(坐标)
背景
做功问题(不能认为没有位移,做功就是0)
概念与性质
定义
公式
意义
几何 (第一型曲线积分分别对x、y坐标轴取积分,在x轴与y轴取不同的函数便得到了第二型曲线积分)
物理 流量平面
https://zhuanlan.zhihu.com/p/
性质 (二维空间为例)
∫ L 1 + L 2 P ( x , y ) d x + Q ( x , y ) d y = ∫ L 1 P ( x , y ) d x + Q ( x , y ) d y + ∫ L 2 P ( x , y ) d x + Q ( x , y ) d y ∫ L P ( x , y ) d x + Q ( x , y ) d y = − ∫ − L P ( x , y ) d x + Q ( x , y ) d y 物理解释: W = ∫ − L F ⋅ d r ⃗ = − ∫ L F ⋅ d r ⃗ \begin{array}{l} \int_{L_{1}+L_{2}} P(x, y) d x+Q(x, y) d y=\int_{L_{1}} P(x, y) d x+Q(x, y) d y+\int_{L_{2}} P(x, y) d x+Q(x, y) d y \\ \\ \int_{L} P(x, y) d x+Q(x, y) d y=-\int_{-L} P(x, y) d x+Q(x, y) d y \quad \text { 物理解释: } W=\int_{-L} F \cdot d \vec{r}=-\int_{L} F \cdot d \vec{r} \end{array} ∫L1+L2P(x,y)dx+Q(x,y)dy=∫L1P(x,y)dx+Q(x,y)dy+∫L2P(x,y)dx+Q(x,y)dy∫LP(x,y)dx+Q(x,y)dy=−∫−LP(x,y)dx+Q(x,y)dy 物理解释: W=∫−LF⋅dr=−∫LF⋅dr
路径无关
等价命题
注意
与路径无关不能说明该积分为0,而是区域D的封闭曲线C的第二类(坐标)曲线积分为0。
D为单连通区域,若是复连通则结论不可用。
- 证明(三种情形)
- X型+Y型
- 封闭曲线
- 按段光滑闭曲线
略…
注解
因为积分与路径无关了,所以我们可以选择任意适合计算的路径进行积分(一般可以选择水平+垂直,这样积分时可固定 x0,y0)
∫ L P ( x , y ) d x + Q ( x , y ) d y = ∫ ( x 0 , y 0 ) ( x 1 , y 1 ) P ( x , y ) d x + Q ( x , y ) d y = ∫ x 0 x 1 P ( x , y 0 ) d x + ∫ y 0 y 1 Q ( x 1 , y ) d y \begin{aligned} \int_{L} P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y &=\int_{\left(x_{0}, y_{0}\right)}^{\left(x_{1}, y_{1}\right)} P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y \\ &=\int_{x_{0}}^{x_{1}} P\left(x, y_{0}\right) \mathrm{d} x+\int_{y_{0}}^{y_{1}} Q\left(x_{1}, y\right) \mathrm{d} y \end{aligned} ∫LP(x,y)dx+Q(x,y)dy=∫(x0,y0)(x1,y1)P(x,y)dx+Q(x,y)dy=∫x0x1P(x,y0)dx+∫y0y1Q(x1,y)dy
对P积分时候y0是确定且固定的,对Q进行积分时候x1是固定的且是确定的,可化简计算
凑微分法 恰当微分方程、积分因子?
若 ∂ Q ∂ x = ∂ P ∂ y , 且存在 u ( x , y ) , 使得 d u ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y , 则 ∫ L P ( x , y ) d x + Q ( x , y ) d y = ∫ ( x 0 , y 0 ) ( x 1 , y 1 ) P ( x , y ) d x + Q ( x , y ) d y = u ( x , y ) ∣ ( x 0 , y 0 ) ( x 1 ⋅ y 1 ) = u ( x 1 , y 1 ) − u ( x 0 , y 0 ) \begin{array}{l} \text { 若 } \frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}, \text { 且存在 } u(x, y), \text { 使得 } \mathrm{d} u(x, y)=P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y, \text { 则 } \\ \begin{aligned} \int_{L} P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y &=\int_{\left(x_{0}, y_{0}\right)}^{\left(x_{1}, y_{1}\right)} P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y \\ &=\left.u(x, y)\right|_{\left(x_{0}, y_{0}\right)} ^{\left(x_{1} \cdot y_{1}\right)} =u\left(x_{1}, y_{1}\right)-u\left(x_{0}, y_{0}\right) \end{aligned}\end{array} 若 ∂x∂Q=∂y∂P, 且存在 u(x,y), 使得 du(x,y)=P(x,y)dx+Q(x,y)dy, 则 ∫LP(x,y)dx+Q(x,y)dy=∫(x0,y0)(x1,y1)P(x,y)dx+Q(x,y)dy=u(x,y)∣(x0,y0)(x1⋅y1)=u(x1,y1)−u(x0,y0)
【例题】
计算方法
封闭且可偏导则格林,是否路径无关?直接算或补线用格林
定积分
参数方程
直线方程 L=f(x),起点x=a,终点x=b
∫ 1. P ( x , y ) d x + Q ( x , y ) d y = ∫ a b { P [ x , φ ( x ) ] + Q [ x , φ ( x ) ] φ ′ ( x ) } d x \int_{1.} P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y=\int_{a}^{b}\left\{P[x, \varphi(x)]+Q[x, \varphi(x)] \varphi^{\prime}(x)\right\} \mathrm{d} x ∫1.P(x,y)dx+Q(x,y)dy=∫ab{
P[x,φ(x)]+Q[x,φ(x)]φ′(x)}dx
参数方程
∫ L P ( x , y , z ) d x + Q ( x , y , z ) d y + R ( x , y , z ) d z = ∫ a β [ P ( x ( t ) , y ( t ) , z ( t ) ) x ′ ( t ) + Q ( x ( t ) , y ( t ) , z ( t ) ) y ′ ( t ) + R ( x ( t ) , y ( t ) , z ( t ) ) z ′ ( t ) ] d t \begin{aligned} & \int_L P(x, y, z) \mathrm{d} x+Q(x, y, z) \mathrm{d} y+R(x, y, z) \mathrm{d} z \\=& \int_a^\beta\left[P(x(t), y(t), z(t)) x^{\prime}(t)+Q(x(t), y(t), z(t)) y^{\prime}(t)+R(x(t), y(t), z(t)) z^{\prime}(t)\right] \mathrm{d} t \end{aligned} =∫LP(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz∫aβ[P(x(t),y(t),z(t))x′(t)+Q(x(t),y(t),z(t))y′(t)+R(x(t),y(t),z(t))z′(t)]dt
【例题】2011数一
【例题】2015数一
公式法
格林公式 二维
沿封闭曲线 C 的线积分与以 C 为边界的平面区域 D 上的双重积分的联系
【例题】
【例题】化空间为平面然后用格林
斯托克斯公式 三维
【例题】2011数一
二 曲面积分
2.1 第一类(面积)
背景
空间曲面的质量(类比二重积分、一型曲线,线的质量)
概念与性质
定义 大S表面积,显然与曲面的方向无关
∬ Σ f ( x , y , z ) d S = lim λ → 0 ∑ i = 1 n f ( ξ i , η i , ζ i ) Δ S i \iint_{\Sigma} {f(x, y, z)} d S=\lim_{\lambda \rightarrow0} \sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}, \zeta_{i}\right) \Delta S_{i} ∬Σf(x,y,z)dS=λ→0limi=1∑nf(ξi,ηi,ζi)ΔSi
性质
线性
(1). ∬ Σ [ f ( x , y ) ± g ( x , y ) ] d S = ∬ Σ f ( x , y ) d S ± ∬ Σ g ( x , y ) d S \iint_{\Sigma}[{f(x, y)} \pm g(x, y)] d S=\iint_{\Sigma} {f(x, y)} d S \pm \iint_{\Sigma} g(x, y) d S ∬Σ[f(x,y)±g(x,y)]dS=∬Σf(x,y)dS±∬Σg(x,y)dS
(2). ∬ Σ 1 + Σ 2 f ( x , y , z ) d S = ∬ Σ 1 f ( x , y , z ) d S + ∬ Σ 2 f ( x , y , z ) d S \iint_{\Sigma_{1}+\Sigma_{2}} {f(x, y, z)} d S=\iint_{\Sigma_{1}} {f(x, y, z)} d S+\iint_{\Sigma_{2}} {f(x, y, z)} d S ∬Σ1+Σ2f(x,y,z)dS=∬Σ1f(x,y,z)dS+∬Σ2f(x,y,z)dS
(3). ∬ Σ d S = S = \iint_{\Sigma} d S=S= ∬ΣdS=S=曲面的面积
奇偶性(只给出一个面,剩余两个同理)
对称性(面是球方程时,类比 y=x 的曲线积分)
计算方法
思路:看能不能特殊替换—投影—对称性奇偶性,注意对称性可能要经过平移—极坐标方程
特殊代替
把曲面方程代入到被积函数里面,简化计算。
【例题】
上面用到了向量积的几何意义是平面四边形的面积,三角形要一半
二重积分法
思想:”以直代曲“,注意微元。注意投影下来的区域不能有重复,熟练之后可以不画出投影直接计算
证明
∵ δ / A = cos γ ∴ A = 1 cos γ δ n ⃗ = ( F ′ x , F ′ y , F ′ z ) , k ⃗ = ( 0 , 0 , 1 ) cos γ = cos < n ⃗ , k ⃗ > = ∣ n ⃗ × k ⃗ ∣ n ⃗ ∣ × ∣ k ⃗ ∣ ∣ = ∣ F ′ z F ′ x 2 + F ′ y 2 + F ′ z 2 ∣ ∵ Z ′ x = − F ′ x F ′ z Z ′ y = − F ′ y F ′ z ∴ cos γ = 1 1 + ( ∂ z ∂ x ) 2 + ( ∂ z ∂ y ) 2 ∴ d A = 1 + ( ∂ z ∂ x ) 2 + ( ∂ z ∂ y ) 2 d δ = 1 + ( ∂ z ∂ x ) 2 + ( ∂ z ∂ y ) 2 d x d y \because δ/A = \cos γ \therefore A = \frac{1}{\cos γ}δ \\ \vec{n} = (F’x,F’y,F’z),\vec{k}=(0,0,1) \\ \cos γ = \cos<\vec{n},\vec{k}> = \left| \frac{\vec{n}\times \vec{k}}{\left|\vec{n} \right| \times \left|\vec{k} \right|} \right| = \left| \frac{F’z}{\sqrt{F’x^2+F’y^2+F’z^2}} \right| \\ \because \quad Z’x = -\frac{F’x}{F’z} \quad Z’y = -\frac{F’y}{F’z} \therefore \cos γ = \frac{1}{\sqrt{1+(\frac{\partial z}{\partial x})^2+(\frac{\partial z}{\partial y})^2}} \\ \therefore dA \ = \ {\sqrt{1+(\frac{\partial z}{\partial x})^2+(\frac{\partial z}{\partial y})^2}}\ dδ \ = \ {\sqrt{1+(\frac{\partial z}{\partial x})^2+(\frac{\partial z}{\partial y})^2}}\ dxdy ∵δ/A=cosγ∴A=cosγ1δn=(F′x,F′y,F′z),k=(0,0,1)cosγ=cos<n,k>=
∣n∣×
k
n×k
=
F′x2+F′y2+F′z2F′z
∵Z′x=−F′zF′xZ′y=−F′zF′y∴cosγ=1+(∂x∂z)2+(∂y∂z)21∴dA = 1+(∂x∂z)2+(∂y∂z)2 dδ = 1+(∂x∂z)2+(∂y∂z)2 dxdy
【例题】 第四卦限,x>0,z>0,y < 0,进而得到x、y的投影区域
2.2 第二类(坐标)
背景
流量问题
概念与性质
定义 单位时间经过指定侧的曲面的流量
注意有方向性,例如一个球体,被积函数为|x|,则在前半部分流量是出去的,为正;在后半球面,由于有绝对值,流量是进去的,为负;这样总体的流量就是0。这里的S的带方向的
性质
线性与方向性,要理解实际意义,这样才能更好的应用对称性
对称性 注意奇倍偶零,应该是dxdy的方向性导致的问题,先记住。出去为正则进入内部为负。
计算方法
思路:画图看对称性奇偶性消除部分参数—补面用高斯或直接投影
二重积分法
第二类-第一类-投影D上的二重积分
【例题】注意y的奇偶性
转换投影
若z=z(x,y),则F = z-z(x,y) 或 F=z(x,y)-z ,看法向量方向。则有平面法向量 : n ‾ = { c o s α , c o s β , c o s γ } = { F x ′ , F y ′ , F z ′ } = { z x ′ , z y ′ , − 1 } 或 { − z x ′ , − z y ′ , 1 } \overline n = \{cos α,cosβ,cosγ\} = \{F’_x,F’_y,F’_z\} = \{z’_x,z’_y,-1\} 或 \ \{-z’_x,-z’_y,1\} n={
cosα,cosβ,cosγ}={
Fx′,Fy′,Fz′}={
zx′,zy′,−1}或 {
−zx′,−zy′,1}。若将S投影到yOz面、xOz面上计算二重积分较困难,可以利用转换公式将其转化到xOy面上进行计算,有
d y d z cos α = d z d x cos β = d x d y cos γ = d S \frac{\mathrm{d} y \mathrm{~d} z}{\cos \alpha}=\frac{\mathrm{d} z \mathrm{~d} x}{\cos \beta}=\frac{\mathrm{d} x \mathrm{~d} y}{\cos \gamma}=\mathrm{d} S cosαdy dz=cosβdz dx=cosγdx dy=dS
。由此可得$ dydz=- z’_x* dxdy, dzdx=- z’_y*dxdy$ 化为二型曲【谁是因变量谁求导,d缺谁乘谁的-偏导】也可以用dS化为一型,记得要单位化
【例题】
高斯公式
联系封闭曲面与三重积分的关系
【例题】补面凑高斯,补面之后通常有部分积分函数是0,不用计算
外侧与上侧
https://www.zhihu.com/question//answer/
2.3 联系
两类曲面积分的联系: ∬ Σ ( P cos α + Q cos β + R cos γ ) d S = ∬ Σ ( P d y d z + Q d z d x + R d x d y ) \iint_{\Sigma}(P \cos \alpha+Q \cos \beta+R \cos \gamma) \mathrm{d} S=\iint_{\Sigma}(P \mathrm{~d} y \mathrm{~d} z+Q \mathrm{~d} z \mathrm{~d} x+R \mathrm{~d} x \mathrm{~d} y) ∬Σ(Pcosα+Qcosβ+Rcosγ)dS=∬Σ(P dy dz+Q dz dx+R dx dy)
【例题】
计算 ∯ S ( x 3 cos α + y 3 cos β + z 3 cos γ ) d S , 其中 S : x 2 + y 2 + z 2 = R 2 , 取外侧 \text { 计算 } \oiint_{S}\left(x^{3} \cos \alpha+y^{3} \cos \beta+z^{3} \cos \gamma\right) \mathrm{d} S \text {, 其中 } S: x^{2}+y^{2}+z^{2}=R^{2} \text {, 取外侧 } 计算 ∬S(x3cosα+y3cosβ+z3cosγ)dS, 其中 S:x2+y2+z2=R2, 取外侧
【解】由两类曲面积分之间的关系得
∯ S ( x 3 cos α + y 3 cos β + z 3 cos γ ) d S = ∯ S x 3 d y d z + y 3 d z d x + z 3 d x d y , 而 ∯ S x 3 d y d z + y 3 d z d x + z 3 d x d y = 3 ∭ Ω ( x 2 + y 2 + z 2 ) d v = 3 ∫ 0 2 π d θ ∫ 0 x d φ ∫ 0 R r 4 sin φ d r = 12 π R 5 5 , 所以 ∮ S ( x 3 cos x + y 3 cos β + z 3 cos γ ) d S = 12 π R 5 5 . \begin{array}{l} \oiint_{S}\left(x^{3} \cos \alpha+y^{3} \cos \beta+z^{3} \cos \gamma\right) \mathrm{d} S=\oiint_{S} x^{3} \mathrm{~d} y \mathrm{~d} z+y^{3} \mathrm{~d} z \mathrm{~d} x+z^{3} \mathrm{~d} x \mathrm{~d} y \text {, } \\ \text { 而 } \oiint_{S} x^{3} \mathrm{~d} y \mathrm{~d} z+y^{3} \mathrm{~d} z \mathrm{~d} x+z^{3} \mathrm{~d} x \mathrm{~d} y=3 \iiint_{\Omega}\left(x^{2}+y^{2}+z^{2}\right) \mathrm{d} v \\ =3 \int_{0}^{2 \pi} \mathrm{d} \theta \int_{0}^{x} \mathrm{~d} \varphi \int_{0}^{R} r^{4} \sin \varphi \mathrm{d} r=\frac{12 \pi R^{5}}{5} \text {, } \\ \text { 所以 } \oint_{S}\left(x^{3} \cos x+y^{3} \cos \beta+z^{3} \cos \gamma\right) \mathrm{d} S=\frac{12 \pi R^{5}}{5} \text {. }\end{array} ∬S(x3cosα+y3cosβ+z3cosγ)dS=∬Sx3 dy dz+y3 dz dx+z3 dx dy, 而 ∬Sx3 dy dz+y3 dz dx+z3 dx dy=3∭Ω(x2+y2+z2)dv=3∫02πdθ∫0x dφ∫0Rr4sinφdr=512πR5, 所以 ∮S(x3cosx+y3cosβ+z3cosγ)dS=512πR5.
注意不能把 x 2 + y 2 + z 2 = R 2 x^{2}+y^{2}+z^{2}=R^{2} x2+y2+z2=R2 代入三重积分,因为三重积分是对Ω的内部进行积分,而R2只是在表面才符合。重积分都不能代入,因为是在内部积分的,线面才可能可以代入。
2020真题
三 格林公式
作用:二维空间沿封闭曲线C的线积分 与 以C 为边界的平面区域D的双重积分 的 联系
两种连通区域
正向边界曲线
当观察者沿着L的正向行走时,D总在他左侧(正向边界曲线可以为顺时针或逆时针),如图11.9和11.10中箭头所示所示。
定理 (圆圈代表积分曲线是封闭曲线)
注意:要确保P、Q在区域D内有一阶连续偏导(原点是奇点不可偏需挖去);连通的区域可以是单连通也可以是多连通(意味着可以补区域使得它连通)
应用
- (记住该结论)格林公式 把 封闭曲线积分转换为 区域面积积分
- 多边形面积
- 逆运用 计算二重积分
注意计算偏导时不要忘记积分函数本身的正负号,及曲线的正负号。
【例题】 (补线 变为封闭曲线)
https://www.zhihu.com/question/
当两个偏导相同,挖奇点的,奇点的二型曲线积分很可能是 2Π
四 斯托克斯
格林公式的三维情况
三维空间对坐标的闭合曲线积分的计算 转换为 曲面积分 进行计算
方向由右手准则确定
背景
这个公式的产生是为了计算物理中的磁场通量,即电场产生磁场,规定线圈逆时针为正方向,用右手定律可知z方向为磁通量正方向,而磁通量可以按照曲面形状分别投影到三个坐标平面进行求取,即三个坐标平面的投影面积乘上相对应的磁通量分量
公式
∮ L P d x + Q d y + R d z \oint_L P d x+Q d y+R d z ∮LPdx+Qdy+Rdz
= ∬ S ( ∂ R ∂ y − ∂ Q ∂ z ) d y d z + ( ∂ P ∂ z − ∂ R ∂ x ) d z d x + ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y =\iint_S\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right) d y d z+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right) d z d x+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y =∬S(∂y∂R−∂z∂Q)dydz+(∂z∂P−∂x∂R)dzdx+(∂x∂Q−∂y∂P)dxdy
= ∬ Σ ∣ cos α cos β cos γ ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R ∣ d S = ∬ Σ ∣ d y d z d z d x d x x d y ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R ∣ =\iint_{\Sigma}\left|\begin{array}{ccc}\cos \alpha & \cos \beta & \cos \gamma \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R\end{array}\right| d S=\iint_{\Sigma}\left|\begin{array}{ccc}d y d z & d z d x & d x x d y \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R\end{array}\right| =∬Σ
cosα∂x∂Pcosβ∂y∂Qcosγ∂z∂R
dS=∬Σ
dydz∂x∂Pdzdx∂y∂Qdxxdy∂z∂R
是平面时候,角度是固定的,用cos,第一型曲面积分(若平行xoy可以直接格林)法向量要单位化;是曲面时候用第二型曲面积分,变成第二型曲面积分后可以继续补面高斯。
【例题】
应用
https://www.zhihu.com/question//answer/
五 高斯公式
高斯公式是斯托克斯公式的特殊形式 ,曲面积分转换为三重积分
基本定理
注意:需要具有连续一阶偏导数,真题09年不可使用
【例题】
计算 ∯ Σ x z 2 d y d z + ( x 2 y − z 3 ) d z d x + ( 2 x y + y 2 z ) d x d y , 其中 Σ 为 z = a 2 − x 2 − y 2 和 z = 0 围成区域的表面外侧. \begin{array}{l}\text { 计算 } \oiint_{\Sigma} x z^{2} \mathrm{~d} y \mathrm{~d} z+\left(x^{2} y-z^{3}\right) \mathrm{d} z \mathrm{~d} x+\left(2 x y+y^{2} z\right) \mathrm{d} x \mathrm{~d} y, \text { 其中 } \Sigma \text { 为 } z=\sqrt{a^{2}-x^{2}-y^{2}} \text { 和 } \\ z=0 \text { 围成区域的表面外侧. }\end{array} 计算 ∬Σxz2 dy dz+(x2y−z3)dz dx+(2xy+y2z)dx dy, 其中 Σ 为 z=a2−x2−y2 和 z=0 围成区域的表面外侧.
【解】由高斯公式得$ \oiint_{\Sigma} x z ^ { 2 } dydz + ( x ^ { 2 } y – z ^ { 3 } ) dzdx + ( 2xy + y ^ { 2 } y ) dxdy$
= ∭ Ω ( x 2 + y 2 + z 2 ) d v = ∫ 0 2 π d θ ∫ 0 π 2 d φ ∫ 0 a r 4 sin φ d r = 2 π 5 a 5 =\iiint_{\Omega}\left(x^{2}+y^{2}+z^{2}\right) \mathrm{d} v=\int_{0}^{2 \pi} \mathrm{d} \theta \int_{0}^{\frac{\pi}{2}} \mathrm{~d} \varphi \int_{0}^{a} r^{4} \sin \varphi \mathrm{d} r=\frac{2 \pi}{5} a^{5} =∭Ω(x2+y2+z2)dv=∫02πdθ∫02π dφ∫0ar4sinφdr=52πa5
无源场
实质是高斯公式,简化一点步骤而已
【例题】2009数一 无源场divF=0,此时三个偏导相加=0,补一个面高斯为0,则原曲面积分即为该补充的面的负积分,通常比较好计算。有奇点,挖去,并令挖去的那个方程可连续偏导从而用两次高斯 880 18
【例题】
六 基本题型
椭圆面积 Πab,椭圆体 4/3Πabc
有圈代表是封闭曲线
曲线
弧长
- 特殊代替
- 参数方程
【例题】
对坐标轴
- 参数方程 / 格林公式
3 880基础解答题4
路径无关
恰当微分方程
- 格林公式(Cr里面x2+4y2=r2是已知的,也可用椭圆面积公式Πab)
曲面
面积
第二类
注意xz时转换为2倍
【例题】2011数一 三种方法
总结
| 曲线积分 | 背景 | 计算方法 | 一般步骤 |
|---|---|---|---|
| 第一类 弧长 | 曲线质量 | 定积分 | 边界代入—对称性、奇偶性—转参 |
| 第二类 坐标 | 做功 | 定积分(参数、直线)、补线用格林 | |
| 第二类 坐标 | 磁通量 | 参数方程、斯托克斯 |
两类曲线积分的区别与联系
物理意义:一个是线的质量、一个是做功,做功有正负,质量没有
联系:dx = ds cosα,可联系两种线积分
曲线
d x = d s ⋅ cos α , d y = d s ⋅ cos β \mathrm{d} x=\mathrm{d} s \cdot \cos \alpha, \mathrm{d} y=\mathrm{d} s \cdot \cos \beta dx=ds⋅cosα,dy=ds⋅cosβ
$\int_L P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y=\int_L[P(x, y) \cos \alpha+Q(x, y) \cos \beta] \mathrm{d}s $
方向
封闭曲线 那做功不是0吗 为什么是Q=P时候才是0?变力做功,虽然起点终点相同,但做功仍然不为0?https://www.zhihu.com/question//answer/
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/124365.html