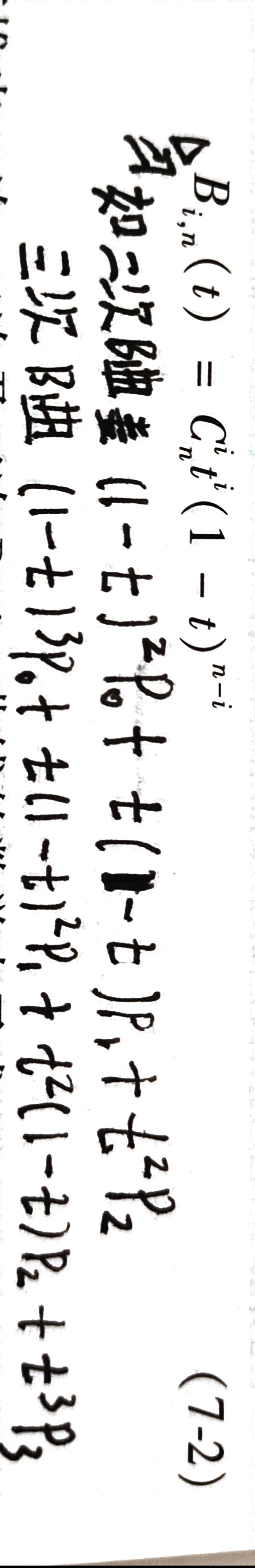【计算机图形学】CSUFT 复习大纲（计算机图形学基础（第2版） 杜晓增 丁宇辰 主编）

大家好，欢迎来到IT知识分享网。

写在最前

计算机辅助设计

CAD，利用它来进行机械零件等设计，可以极大提高设计效率

用户接口

人与计算机“交流”的平台，人们通过这一平台将指令发送给计算机，计算机通过这一平台反馈结果
早期是基于文本的
现在采用图形化用户接口

科学可视化

在大型科学计算中数据量极大，如果能将这些结果数据以图形形式绘制出来，并将处理过程用动画方式实时表现，就会很容易看出其变化规律

图形核心系统

GKS,提供在应用程序和图形IO设备之间的功能接口，定义了一个独立于高级程序设计语言的图形系统
功能主要有：
控制功能 工作站的打开、关闭、激活、删除等
变换功能
图段功能
应用程序

OpenGL

一个开放的针对图形硬件的三维图形软件包
主要功能：
图形建模
图形变换
光照、材质、纹理和像素操作
融合、反走样和雾化等效果

图形输入设备

键盘和鼠标
光笔 通过检测CRT屏幕上的某一点的光来选定屏幕的位置
数字化仪 平板数字化仪（手绘板）
扫描仪 将图形、图像和文字通过光电扫描技术输入计算机
数码相机

输入设备

向图形软件输入图形命令
按输入的信息的不同性质（P67）
定位设备
用来指定用户空间的一个位置，比如说用来指定一条线段的端点
笔画设备
又称描画设备，用于指定一组有序的点的位置，如用来指定一个多边形的顶点组
选择设备
用来在应用程序的多个选项中选定一项，如用来选择菜单的某一选项
输入方式有：直接或间接在屏幕上进行，字符串名称，手写输入，时间扫描，声音输入。
选择设备对应的物理设备有：触摸屏，数字化仪，光笔，鼠标，操纵杆，跟踪球，编程功能键，字符串输入设备，声音识别仪
字符设备
又称字符串设备，用来向应用程序输入字符串
输入方式有：键盘输入，手写输入，声音输入，菜单输入
对应的物理设备有：键盘，数字化仪，光笔，声音识别仪
定值设备
用来为应用程序输入一个数值（实数），如在缩放时输入一个比例因子
拾取设备
用来在处理的模型中选取一个对象，为应用程序的操作处理确认目标

图形输出设备

绘图仪、激光打印机、喷墨打印机

图形显示设备

用以显示图形和文字，目前主要有CRT（阴极射线管）和LCD（液晶显示）两种

阴极射线管 CRT

工作原理：
电子枪发出电子束，通过聚焦系统和偏转系统，射向涂有荧光材料的屏幕的指定位置。在电子束轰击的位置，荧光屏发出一个小的光点。图像就是由屏幕上许许多多不同亮度和颜色的光点构成的。
由于光点的亮度会随着时间的推移而逐渐衰减，为了保证屏幕上可以显示稳定的图像，电子束就必须以一定的速度反复不断地轰击（重绘）图像，使光点保持相对稳定的亮度。（也称作刷新）
根据电子束的运动方式，刷新式CRT分为以下两种：
随机扫描显示器
电子束的运动方向不确定，是由所绘图形的形状决定的。
优点是可以绘制高质量线条，特别适合由直线段构成的图形
缺点是所绘制的图形由长短不一的直线段构成，无法较好表现复杂的曲线，更无法表现色彩丰富、具有真实感的图形和视频动画
光栅扫描显示器
电子束的运动方向是固定的，从上到下，由左至右扫描整个屏幕，图形由点阵构成，
优点是可以显示高质量图片，表现色彩丰富，真实的图片视频。
缺点是会发生走样，产生锯齿状。

刷新式显示器的相关术语

点距
荧光屏上两个相同颜色的荧光点间的距离
场频
垂直扫描频率，即通常所说的屏幕刷新率。理解为每秒重画屏幕的次数，频率越高，图像稳定性越好。
行频
电子枪每秒在荧光屏上扫描过的水平线数量：行数*场频
800*600分辨率，85Hz的显示器，行频至少为 600 * 85Hz = 51kHz
带宽
每秒电子枪扫过的总像素：水平分辨率 * 垂直分辨率 * 场频
上述式子只是理论值，实践中，为了避免图像边缘的信号衰减，保持图像四周清晰，电子枪的扫描能力要大于分辨率，通常水平方向大25%，垂直方向大8%
即实际带宽公式：125%水平分辨率 * 108%垂直分辨率 * 场频

区域填充算法

多边形的扫描线连贯算法

定义

对于一个多边形，用一组水平或垂直的扫描线进行扫描，求出每条扫描线与多边形的交点，这些交点将扫描线分割线段，将落在多边形内的所有线段上的每个像素点赋以给定的多边形填充色。简单来说就是用一段水平的扫描线，从下往上扫描一个多边形，将扫描线与多边形的交点记录，并用像素填上。

算法步骤

1. 确定多边形所占有的最大扫描线数，得到多边形顶点的最小和最大y值（y min和y max）。
2. 从y = y min 到 y = y max 进行扫描，每次用一条扫描线进行填充。

• 我们需要建立两个表：边表(ET)和活动边表(AET)，即使用有序边表算法对扫描线进行转化。
• 边表：用来对除水平边外的所有边进行登记，来建立边的记录。 它的结构一般是这样↓
• 
• 活动边表：当对某一条扫描线进行扫描转换时，我们只需要考虑与它相交的那些边线，为此需要建立一个只与当前扫描线相交的边记录链表，称之为活动边表
  

种子填充算法

几何变换

引入齐次坐标后点平移的矩阵变换为：

缩放：



相对于任意直线的对称变换

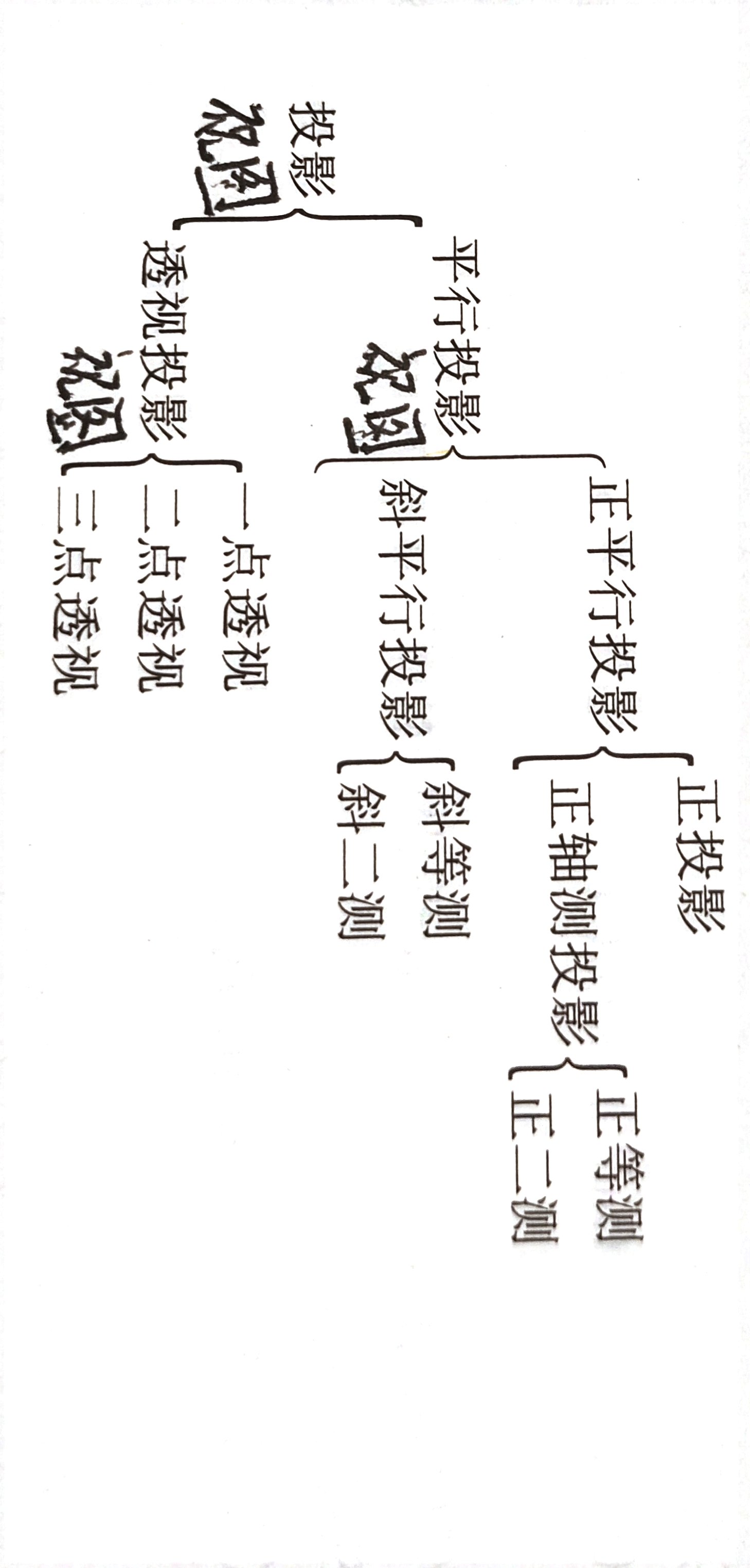
投影变换

投影变换目的就是把场景世界中的3D物体转换为2D平面图形的过程，转换后降了一维。
投影中心：发出投影线的点

分类

按投影中心和投影面的距离远近可分为以下两种：
平行投影
投影中心和投影面的距离无穷大
透视投影
投影中心和投影面的距离是有限的

正平形投影

投影中心距投影面的距离无穷大，投影线垂直于投影面
正平行投影变换：
点（x,y,z）在xoy平面的正投影只需要去掉z坐标，为（x，y).
正平行投影的变换矩阵：

正试图变换，直接乘变换矩阵
侧视图变换，先将物体绕 y 轴选择 -90°（顺时针），再乘变换矩阵
俯视图变换，先将物体绕 y 轴选择 90°（逆时针），再乘变换矩阵
Ps: 旋转的右手定则：拇指指向旋转轴的正方向，其余四指弯曲的方向为逆时针。

正轴测投影

轴测投影是要同时表现三维物体的长、宽、高三个参数。

投影面与三个坐标轴之间的夹角都相等的时候，是等轴测。
投影面与两个坐标轴之间的夹角相等就是正-=二测，如与X和Y轴的夹角相等时，投影的长和宽与原图形保持一致。
投影面如果与三个坐标轴之间的夹角都不同,就是正三侧。

斜平形投影

投影中心距投影面的距离无穷大，投影线不垂直于投影面。
斜等侧图的投影方向与投影平面的夹角是45度角。

透视投影

投影中心距投影面的距离有限

图形裁剪

窗口

用户用来定义设计对象的实数域统称为用户域，也称为用户空间
用户在用户域中指定任意的区域w，把他感兴趣的这部分用户域内的图形输出到屏幕上，这部分区域称为窗口区。

视区

图形设备上用来输出图形的最大区域称为屏幕域，任何小于或等于屏幕域的区域可以定义为视区。

线段裁减

标号法

Cohen-Sutherland算法

核心思想：通过编码测试来减少计算交点的次数。（编码算法）

线段端点以区域赋值以四位二进制码。

• 编码顺序：四位从右到左分别为：左边界、右边界、下边界、上边界。
• 编码值：落在相应位置为1，否则为0
• 

对P1和P2点按对应的区域编码为C1和C2
根据线段端点的区域码快速判断：
C1 | C2=0: 表示两个端点区域码都为0000，线段在窗口内，直接返回。（如P5P6）
C1 & C2 !=0: 表示两个 端点区域码有同样的位置都为1，完全在窗口外，全部舍弃，返回。(如P9P10)
不能确定完全在窗口内外的线段–>求交(如P1P2、P3P4、P7P8)
方法是：首先对线段外端点（落在窗口外的点）与一条裁剪边界比较来确定需要裁剪多少线段；然后，将线段的剩下部分与其他裁剪边界对比，直到该直线完全落在窗口内或者被舍弃。（即计算出直线与窗口的交点，将直线分段后继续进行检测判断，逐段舍弃位于窗口外的线段，保留窗口内的线段）
要点：始终保证P1为落在窗口外的点，将P1与窗口边界求交。

中点法

利用编码来检测图形是否可见
对于完全在窗口外和完全在窗口外的线段都是简单的舍弃或保留。
对于不能确定完全在窗口内外的线段，将直线按中点分成相等的两部分，再判断分离出来的两直线，如果两直线都不能舍弃或保留，就搁置其中一条，对另一条再进行中点再分，求出其可见线段，对搁置的那一条直线求出可见线段，并把这两线段连线。

多边形裁剪

Bezier曲线（贝塞尔曲线）

特点

控制点的输入与曲线输出之间的关系明确，使设计人员比较直观地估计给定条件与设计出曲线之间的关系。
Bezier曲线的形状是由一组多边折线的顶点唯一定义出来的，改多边折线称为特征多边形。

定义

给定空间n+1个点的位置矢量P i （ i = 0 , 1 , 2 , … , n ），则Bezier参数曲线上各点坐标的插值公式是：

P i 构成该Bezier曲线的特征多边形
B i , n ( t ) 是n次Bernstein（伯恩斯坦）基函数

性质

端点性质
端点位置矢量
Bezier曲线的起点、终点与相应的特征多边形的起点、终点重合。
切矢性
Bezier曲线在起点、终点处的切线方向与相应的特征多边形的第一条边和最后一条边走向一致。
二阶导矢
2阶导矢只与相邻的3个顶点有关，事实上，r阶导矢只与（r+1）个相邻点有关，与更远点无关。
对称性
n次Bezier曲线的顶点位置不变，而报次序颠倒，此时的Bezier曲线与原Bezier曲线形状相同，走向相反。
凸包性
在几何图形上，意味着Bezier曲线Pt)在t [0，1]中各点是控制点P的凸线性组合，即曲线落在特征多边形顶点P构成的凸包之中。
几何不变性
曲线的形状仅与特征多边形顶点的相对位置有关，与坐标系的选择无关。

可见面判断

直线的生成

DDA算法

对于x增长快的情况：

对于y增长快的情况：

// 数值微分方法绘制直线段 abs（）绝对值 void DDAline(int x0, int y0, int x1, int y1) { 
    int dx = x1 - x0; int dy = y1 - y0; int epsl, k; // 横向和纵向上的距离 float x = x0, y = y0, xIncre, yIncre; if (abs(dx) > abs(dy)) epsl = abs(dx); else epsl = abs(dy); xIncre = (float)(dx) / epsl; yIncre = (float)(dy) / epsl; glBegin(GL_POINTS); for (k = 0; k <= epsl; k++) { 
    dc.SetPixel((int)(x + 0.5), (int)(y + 0.5)); // 舍入取整,画点 x += xIncre; y += yIncre; // 每次叠加一个增量 } glEnd(); } 

Bresenham算法

由Bresenham提出的一种精确而有效的光栅线生成算法，可用于显示线、圆和其他曲线的整数增量运算。它是目前最有效的线段生成算法。
K<1 dx>0;当K>1时交换X,Y；dx变dy，dy变dx
abs（）绝对值
e>0时 Y(i+1)=(Yi)+1
e<0时 Y(i+1)=(Yi)
e(i+1)=ei+2dy-2[Y(i+1)-(Yi)]dx

void bresenham(int x1,int y1,int x2,int y2){ 
    int i,x,y,dx,dy; float e; dx=x2-x1; dy=y2-y1; e=2*dy-dx; for(i=1;i<=dx;i++){ 
    x++; e=e+2dy; if(e>0){ 
    y++; e=e-2*dx; } } }