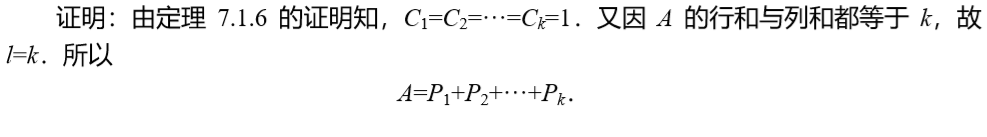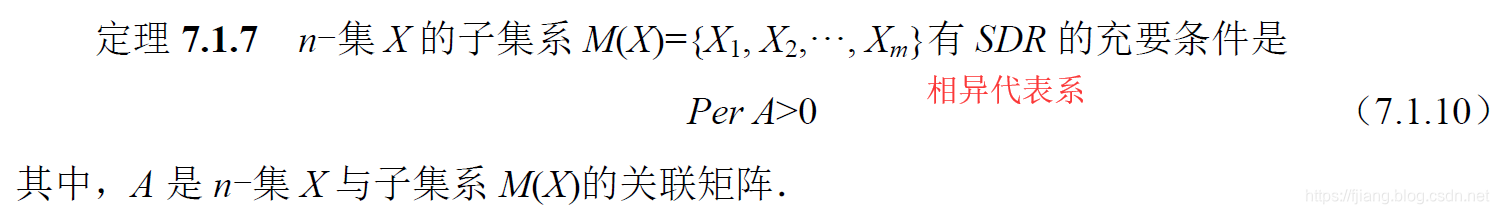组合数学（2）——组合矩阵

大家好，欢迎来到IT知识分享网。

0. (0,1)矩阵

1. 关联矩阵

1.1. 置换、置换矩阵和置换方阵

这里为什么突然又讲置换了呢？因为关联矩阵的很多性质和置换有关。

在组合数学中，置换一词的传统意义是一个有序序列，其中元素不重复，但可能有阙漏。例如1,2,4,3可以称为1,2,3,4,5,6的一个置换，但是其中不含5,6。此时通常会标明为“从n个对象取r个对象的置换”。

1.2. 置换矩阵的性质

上面是给出了置换矩阵和方阵的定义，下面说说置换矩阵的3条性质。

• 关于大小的性质
  
  从这个定理中，可以知道置换矩阵都是一个扁的长方形矩阵，下面给出证明：
  
  
  
  
• 关于形状的性质
  
  这里介绍了置换矩阵的样子，也就是每行恰好只有1个1，其他全为0，而每列不能超过1个1。这其实也是一个保持矩阵置换后，行列不会出现相加减的情况。为定理7.1.3打下基础。下面给出证明：
  
  
  
  
• 关于置换矩阵的作用的性质
  
  这个就是很明显了，为了完成矩阵的置换，其实就是调换矩阵的行与列的位置。尽管这些我们都明白，但是我们还是要给出证明：
  
  
  
  

1.3. 关联矩阵的性质

• 关联矩阵左右相乘的意义：
  这告诉我们$A{A}^T$的意义是获得两两子集的交集的元素数量，而$A^{T}A$的意义是包含两两元素的子集的个数，这两者正好是个相反的操作。下面给出证明：
  
  
  
• 矩阵的线秩和项秩
  在给出定理7.1.5之前，我们首先介绍矩阵的线秩和项秩：
  项秩(term rank)是矩阵的一个指标，设A是m×n的(0，1)矩阵，A中两两不在同一线(矩阵的一行或一列都称为矩阵的一条线)上的1的最大个数称为A的项秩。
  线秩(line rank)是矩阵的一个指标，设A是m×n的(0，1)矩阵，A的行与列统称为线，包含A的全部1的最小线数称为A的线秩。
  
  
  

• 置换矩阵的应用
  
  可以看到，这其实就是使用l个置换矩阵P进行拟合一个特定的矩阵。其证明如下：
  
  这里可以推出关于（0,1）方阵的特殊性质：
  
  这里只是上面定理的一个特殊例子，同样适用于双随机矩阵相关性质的证明。证明如下：
  
  
  
  
  
  
  
  

2 积和式

• 积和式Per A的性质1
  
  这个性质解释了积和式与相异代表系之间的关系，下面给出证明：
  
  而且，相异代表系的个数等于其积和式：
  
  下面给出证明（真的是一个定理一个证明）：
  
  
  
  
  
  
  
  
• 积和式与常数的乘法
  
  其实和矩阵与常数的乘法一样，下面给出证明：
  
  
  
  
• 积和式的恒等变换
  
  交换行列位置，最后还是这些数，当然是相等的，就像行列式一样的。
  
  
• 积和式按位相加
  
  这些都是和行列式类似的证明方法，这里不做更细节的证明。
  
  

3. （0,1）矩阵类U（R,S）