大家好,欢迎来到IT知识分享网。
菲涅尔定理及MATLAB实现
本文是学习胡章芳《MATLAB仿真及其在光学课程中的应用》和赵凯华《光学》这两本书时所做笔记。
1. 菲尼尔反射与折射公式
图1. 入射光,反射光和折射光内
p p p、
s s s、
k ^ \hat{k} k^正交系数的选取
按照以上条件,可由电磁场的边值条件可以导出,在界面两侧邻近点的入射场、反射场合折射各分量满足以下关系,即菲涅尔反射折射公式:
E ~ 1 p ′ = n 2 c o s i 1 − n 1 c o s i 2 n 2 c o s i 1 + n 1 c o s i 2 E ~ 1 p = t a n ( i 1 − i 2 ) t a n ( i 1 + i 2 ) E ~ 1 p {\tilde{
{E}}}_{1p}^{‘}=\frac{n_{2}cosi_{1}-n_{1}cosi_{2}}{n_{2}cosi_{1}+n_{1}cosi_{2}}{\tilde{
{E}}}_{1p}=\frac{tan(i_{1}-i_{2})}{tan(i_{1}+i_{2})}{\tilde{
{E}}}_{1p} E~1p′=n2cosi1+n1cosi2n2cosi1−n1cosi2E~1p=tan(i1+i2)tan(i1−i2)E~1p
E 2 p ~ = 2 n 1 c o s i 1 n 2 c o s i 1 + n 1 c o s i 2 E 1 p ~ \tilde{E_{2p}}=\frac{2n_{1}cosi_{1}}{n_{2}cosi_{1}+n_{1}cosi_{2}}\tilde{E_{1p}} E2p~=n2cosi1+n1cosi22n1cosi1E1p~
E ~ 1 s ′ = n 1 c o s i 1 − n 2 c o s i 2 n 1 c o s i 1 + n 2 c o s i 2 E ~ 1 s = s i n ( i 2 − i 1 ) s i n ( i 2 + i 1 ) E ~ 1 s {\tilde{
{E}}}_{1s}^{‘}=\frac{n_{1}cosi_{1}-n_{2}cosi_{2}}{n_{1}cosi_{1}+n_{2}cosi_{2}}{\tilde{
{E}}}_{1s}=\frac{sin(i_{2}-i_{1})}{sin(i_{2}+i_{1})}{\tilde{
{E}}}_{1s} E~1s′=n1cosi1+n2cosi2n1cosi1−n2cosi2E~1s=sin(i2+i1)sin(i2−i1)E~1s
E ~ 2 s ′ = 2 n 1 c o s i 1 n 1 c o s i 1 + n 2 c o s i 2 E ~ 1 s = 2 c o s i 1 s i n i 2 s i n ( i 2 + i 1 ) E ~ 1 s {\tilde{
{E}}}_{2s}^{‘}=\frac{2n_{1}cosi_{1}}{n_{1}cosi_{1}+n_{2}cosi_{2}}{\tilde{
{E}}}_{1s}=\frac{2cosi_{1}sini_{2}}{sin(i_{2}+i_{1})}{\tilde{
{E}}}_{1s} E~2s′=n1cosi1+n2cosi22n1cosi1E~1s=sin(i2+i1)2cosi1sini2E~1s
菲涅尔公式表明,反射、折射光里的p分量只与入射光里的p分量有关,s分量只与s分量有关。这表明在反射、折射的过程中p、s两个分量的振动是相互独立的。
2. 反射率和透射率
为了说明反射和折射各占多少比例,引入反射率与透射率概念。当p和s这两个分量的反射率和透射率被确定,则任意方向上的振动的光的反射、折射特性也即确定。
| p分量 | s分量 | |
|---|---|---|
| 振幅反射率 | r ~ p = E ′ ~ 1 p / E ~ 1 p {\tilde{r}_{p}=\tilde{ {E}’}_{1p}/\tilde{ {E}}_{1p}} r~p=E′~1p/E~1p |
r ~ s = E ′ ~ 1 s / E ~ 1 s {\tilde{r}_{s}=\tilde{ {E}’}_{1s}/\tilde{ {E}}_{1s}} r~s=E′~1s/E~1s |
| 振幅透射率 | t ~ p = E ~ 2 p / E ~ 1 p {\tilde{t}_{p}=\tilde{ {E}}_{2p}/\tilde{ {E}}_{1p}} t~p=E~2p/E~1p |
t ~ s = E ~ 2 s / E ~ 1 s {\tilde{t}_{s}=\tilde{ {E}}_{2s}/\tilde{ {E}}_{1s}} t~s=E~2s/E~1s |
| 将菲涅尔反射折射公式代入振幅反射率和透射率公式,即可得到 r ~ p {\tilde{r}_{p}} r~p、 r ~ s {\tilde{r}_{s}} r~s、 t ~ p {\tilde{t}_{p}} t~p、 t ~ s {\tilde{t}_{s}} t~s、的具体表达式: |
{ r p ~ = n 2 c o s i 1 − n 1 c o s i 2 n 2 c o s i 1 + n 1 c o s i 2 = t a n ( i 1 − i 2 ) t a n ( i 1 + i 2 ) r s ~ = n 1 c o s i 1 − n 2 c o s i 2 n 2 c o s i 1 + n 2 c o s i 2 = s i n ( i 2 − i 1 ) s i n ( i 2 + i 1 ) \left\{\begin{matrix} \tilde{r_{p}}=\frac{n_{2}cosi_{1}-n_{1}cosi_{2}}{n_{2}cosi_{1}+n_{1}cosi_{2}}=\frac{tan(i_{1}-i_{2})}{tan(i_{1}+i_{2})}\\ \tilde{r_{s}}=\frac{n_{1}cosi_{1}-n_{2}cosi_{2}}{n_{2}cosi_{1}+n_{2}cosi_{2}}=\frac{sin(i_{2}-i_{1})}{sin(i_{2}+i_{1})} \end{matrix}\right. {
rp~=n2cosi1+n1cosi2n2cosi1−n1cosi2=tan(i1+i2)tan(i1−i2)rs~=n2cosi1+n2cosi2n1cosi1−n2cosi2=sin(i2+i1)sin(i2−i1)
{ t p ~ = 2 n 1 c o s i 1 n 2 c o s i 1 + n 1 c o s i 2 t s ~ = 2 n 1 c o s i 1 n 1 c o s i 1 + n 2 c o s i 2 \left\{\begin{matrix} \tilde{t_{p}}=\frac{2n_{1}cosi_{1}}{n_{2}cosi_{1}+n_{1}cosi_{2}}\\ \tilde{t_{s}}=\frac{2n_{1}cosi_{1}}{n_{1}cosi_{1}+n_{2}cosi_{2}} \end{matrix}\right. {
tp~=n2cosi1+n1cosi22n1cosi1ts~=n1cosi1+n2cosi22n1cosi1
上式中各个光波分量应是瞬时值,也可被看成是复振幅,因为它们的时间和频率是相同的。
3. MATLAB实现
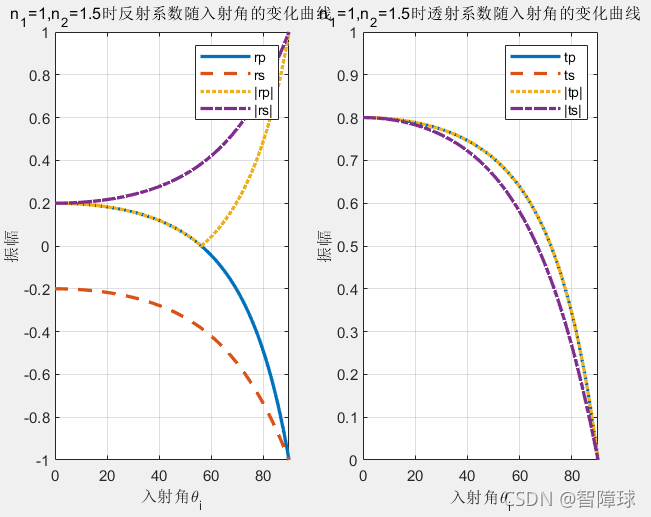
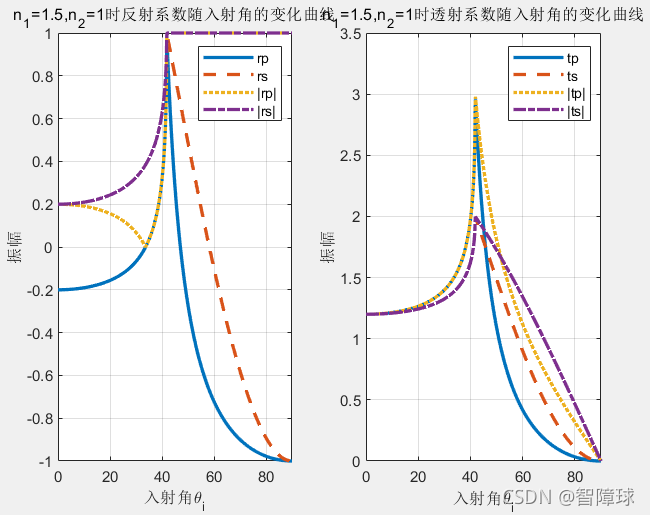
已知界面两侧的折射率n1、n2和入射角θ1,绘出在n1<n2(光由光疏介质射向光密介质)和n1>n2(光由光密介质射向光疏介质)两种情况下,反射系数、透射系数随入射角θi的变化曲线。
clear; %清空内存空间 disp('请输入介质折射率n1和n2') n1=input('n1='); %接受键盘任意输入合适的折射率n1 n2=input('n2='); %接受键盘任意输入合适的折射率n2 theta = 0:0.1:90; %入射角范围0-90°,步距0.1° a=theta*pi/180; %角度化为弧度 rp =(n2*cos(a)-n1*sqrt(1-(n1/n2*sin(a)).^2))./... (n2*cos(a)+n1*sqrt(1-(n1/n2*sin(a)).^2)); %p分量振幅反射率 rs = (n1*cos(a)-n2*sqrt(1-(n1/n2*sin(a)).^2))./... (n1*cos(a)+n2*sqrt(1-(n1/n2*sin(a)).^2)); %s分量振幅反射率 tp = 2*n1*cos(a)./(n2*cos(a)+n1*sqrt(1-(n1/n2*sin(a)).^2));%p分量振幅透射率 ts = 2*n1*cos(a)./(n1*cos(a)+n2*sqrt(1-(n1/n2*sin(a)).^2));%s分量振幅透射率 figure(1); %图形窗口 subplot(1,2,1); %作图rp、rs、|rp|、|rs|随入射角的变化曲线 plot(theta,rp,'-',theta,rs,'--',theta,abs(rp),':',... theta,abs(rs),'-.','LineWidth',2); legend('rp','rs','|rp|','|rs|'); xlabel('入射角\theta_i'); ylabel('振幅'); title(['n_1=',num2str(n1),',n_2=',num2str(n2),'时反射系数随入射角的变化曲线']); axis([0 90 -1 1]); %设定作图区间 grid on; %作图加栅格 subplot(1,2,2); %作图tp、ts、|tp|、|ts|随入射角的变化曲线 plot(theta,tp,'-',theta,ts,'--',theta,abs(tp),':',... theta,abs(ts),'-.','LineWidth',2); legend('tp','ts','|tp|','|ts|'); xlabel('入射角\theta_i'); ylabel('振幅'); title(['n_1=',num2str(n1),',n_2=',num2str(n2),'时透射系数随入射角的变化曲线']); if n1<n2 axis([0 90 0 1]); %设定作图区间 else axis([0 90 0 3.5]); %设定作图区间 end grid on; %作图加栅格
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/124843.html