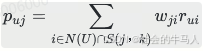推荐系统实践——利用用户行为数据

大家好，欢迎来到IT知识分享网。

第二章利用用户行为数据

2.1 用户行为数据简介

基于用户行为数据分析的推荐算法在学术上也称协同过滤算法

用户行为数据最简单的存在形式为日志

用户行为：显性反馈行为（直接评分）和隐性反馈行为（页面浏览行为）

数据集：（1）无上下文的隐性反馈数据集：仅包含用户ID和物品ID；

（2）无*显性*：用户ID、物品ID、用户对物品评分；

（3）有隐性：用户ID、物品ID和用户对物品产生行为的时间戳；

(4)有显性：用户ID、物品ID和用户对物品评分和评分行为发生的时间戳；

2.2 用户行为分析

设计算法前，需先对数据进行分析，了解规律后才能着手算法的设计。

用户活跃度与物品流行度的分布同样满足长尾分布。

活跃度和流行度的关系

协同过滤算法：基于用户和基于物品的。

2.3 协同过滤算法

2.3.1 UserCF：分析不同用户之间的相似度进行推荐；

算法步骤：（1）首先找到和目标用户相似的用户集合

（2）找到这个集合中用户，喜欢且目标用户没听说过的物品推荐给目标用户；

对用户u推荐N个物品记为R，用户u在测试集上喜欢的物品合集为T

评测指标： 召回率：R和T的交集/T

准确率：R和T的交集/R

覆盖率：所有的R中物品种类的总数/所有物品总数

新颖度：推荐的物品中的流行度越高，新颖度越低

由于普通的余弦相似度计算的时间复杂度太大，因此需建立物品到用户的倒排表，userCF定义用户的相似度为：

$w_{uv}=\frac{|N(u)\cap N(v)|}{\sqrt{|N(u)| | N(v)|}}$

其中，N(u)表示用户u曾有过正反馈的物品集合，N(v)为用户v曾有过正反馈的物品集合。由于该公式过于粗糙，同时热门物品会对相似度产生影响，因此采用如下公式：

$w_{uv}=\frac{\sum_{i\in N(u)\cap N(v)}\frac{1}{log(1+|N(i)|)}}{\sqrt{|N(u)||N(v)|}}$

这样就惩罚了用户u和用户v共同兴趣列表中热门物品对他们相似度的影响

通过计算用户对每个物品的兴趣度：

$p(u,i)=\sum_{v\in S(u,k) \cap N(i)}w_{uv}r_{vi}$

其中，S(u,K)包含和用户u兴趣最接近的K个用户，N(i)是对物品侑过行为的用户集合，Wuv是用户u和用户v的兴趣相似度，rvi代表用户V对物品i的兴趣，由于使用的是单一行为的隐反馈数据，所以所有的rvi=1。

用户相似度改进：N(i)—>1/log（1+N(i)）,用于惩罚用户u和用户i共同兴趣列表中热门物品对他们相似度的影响。改进之后UserCF—->User-IIF。

2.3.2 ItemCF：分析用户行为记录计算出物品之间的相似度。

算法步骤：（1）计算物品相似度：利用 $$\frac{|N(i)\cap N(j)|}{|N(i)||N(j)|}” />

惩罚物品j的权重，防止热门物品与其他物品之间相似度过高；

（2）根据物品相似度和用户历史数据为用户生成推荐列表：同样利用倒排表实现；

在得到物品之间的相似度后，利用如下公式计算用户u对物品j的兴趣：

其中，Puj表示用户u对物品j的兴趣,S(j,k)表示和物品j最相似的k个物品,N(u)表示用户产生过行为的物品集合,rui表示用户u对物品是否产生过行为(对于评分系统,可以表示u对i的评分,wji是物品j和i的相似度

其中k对算法性能的影响：

1、合适的k能有效增加精度；

2、流行度：不是完全正相关，开始会随着k值的增加而提高，到一定程度不会变化；

3、k值得增加会导致覆盖率的下降。

活跃用户对物品的相似度的贡献应该不小于不活跃的用户，因此修正后的物品相似度计算公式：

$w_{ij}=\frac{\sum_{u\in N(i)\cap N(j)}\frac{1}{log(1+|N(u)|)}}{\sqrt{|N(i)||N(j)|}}$

使用惩罚来修正物品相似度，比如书店老板购买的书籍并不能说明他对每本书的兴趣。

在得到相似度后，利用如下公式计算用户兴趣度：

$p(u,j)=\sum_{i\in S(u,k) \cap N(u)}w_{ji}r_{ui}$

其中N（u）是用户喜欢的物品的集合,S(j,k)是和物品j最相似的k个物品的集合，Wji是物品j和i的相似度，rui是用户u对物品i的兴趣。该公式的含义是，和用户历史上感兴趣的物品越相似的物品，越有可能在用户的推荐列表中获得比较高的排名。

哈利波特问题：过于热门导致购买任何一本书的人都会购买；

解决方法：加大惩罚度。

$w_{ij}=\frac{|N(i)\cap N(i)|}{{|N(i)|^{1-\alpha} | N(j)|^\alpha}}$

然而仅仅依靠此方法并不能彻底解决哈利波特问题，比如不同领域的最热门物品之间往往具有比较高的相似性，因此还需要引入物品的内容数据来解决此问题，比如通过对不同领域的物品降低权重，但这并非协同过滤的讨论范畴。

总结：

UserCF：特点

性能：适用于用户较少的场合，如果用户很多，计算用户相似度矩阵代价很大。
领域：时效性较强，用户个性化兴趣不太明显的领域。
实时性：用户有新行为，不一定造成推荐结果的立即变化。
冷启动：
1. 在新用户对很少的物品产生行为后，不能立即对它进行个性化推荐，因为用户相似度表示每隔一段时间离线计算的。
2. 新物品上线后一段时间，一旦有用户对物品产生行为，就可以将新物品推荐给和对它产生行为的用户兴趣相似的其他用户。
推荐理由：很难提供令用户信服的推荐解释。

ItemCF：特点

性能:适用于物品数明显小于用户数的场合，如果物品很多，计算物品的相似度矩阵代价很大。
领域：长尾物品丰富，用户个性化需求强烈的领域。
实时性：用户有新行为，一定会导致推荐结果的实时变化。
冷启动：
1. 新用户只要对一个物品产生行为，就可以给它推荐和该物品相关的其它物品。
2. 但没有办法在不离线更新物品相似度表的情况下将新的物品推荐给用户。
推荐理由：利用用户的历史行为给用户做推荐解释，可以令用户比较信服。

2.4 隐语义模型

usercf：需要找到兴趣相似的用户，然后推荐用户喜欢的其他书；（用户相似度）

itemcf：需要相似物品的书，然后推荐给用户没有看过的书；（物品相似度）

从数据出发，自动找到类，然后进行个性化推荐，称之为隐含语义分析技术，著名的模型和方法有PLSA、LDA、隐含类别模型、隐含主题模型、矩阵分解。

在隐性反馈数据集上应用LFM解决TopN推荐。

LFM利用如下公式计算用户u对物品i的兴趣：

$Preference(u,i)=r_{ui}=p_{u}^T q_i=\sum_{k=1}^K p_{u,k}q_{i,k}$

其中 $p_{u,k}$ 和 $q_{i,k}$ 是模型的参数，其中 $p_{u,k}$ 度量用户u的兴趣和第k个隐类的关系， $q_{i,k}$ 度量了第k个隐类和物品i之间的关系。举例如下：

在隐性反馈数据集上应用LFM解决TopN推荐的第一个关键问题:给用户生成负样本；

最好的方法是：

1）对每个用户需保证正负样本的平衡。

2）采样负样本时要选取那些热门但是用户却没有行为的物品。

负样本采样过程：

def RandomSecNega(self，items)： ret =dict（） for i in items.keys(): ret[i]=1 n=0 for i in range(0,len(items)*3)： item=items_pool[random.randint(0,len(items_pool)-1)] if item in ret: Continue ret[item]=0 n+=1 if n>len(items): Break return ret

经过采样后，得到一个用户-物品集K={(u,i)},通过如下损失函数优化迭代找到合适的P和Q:

$C=\sum_{(u,i)\in K}(r_{ui}-r_{ui}^{'})^2=\sum_{(u,i)\in K}(r_{ui}-\sum_{k=1}^K p_{u,k}q_{i,k})^2+\lambda||p_u||^2+\lambda||q_i||^2$

其中， $\lambda||p_u||^2+\lambda||q_i||^2$ 用于防止过拟合的正则项， $$\lambda$$通过实验获得。利用随机梯度下降算法来最小化损失函数。

首先对他们分别求偏导数：

$f(C,p)=-2q_ik*e_{ui}+2\lambda p_{uk}$

$f(C,q)=-2p_uk*e_{ui}+2\lambda q_{ik}$

因此可以得到如下：

$p_{uk}=p_{uk}+\alpha(q_{ik}*e_{ui}-\lambda p_{uk})$

$q_{ik}=p_{ik}+\alpha(p_{uk}*e_{ui}-\lambda p_{ik})$

其中, $\alpha$ 为学习速率，此参数的选取需经过反复实验获得。

2.5 基于图的模型

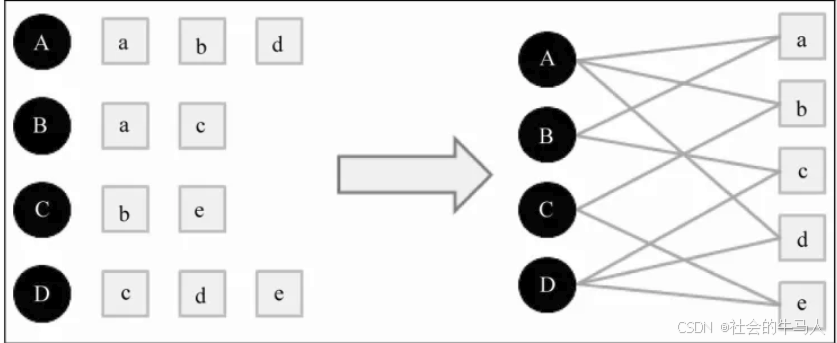
用户行为二分图：

顶点的相关性取决于三个因素：

1.两个顶点之间的路径数

2.两个顶点之间路径的长度

3.两个顶点之间的路径经过的顶点

相关性搞得一对顶点一般具有如下特征：

1.两个顶点之间有很多路径相连；

2. 连接两个顶点之间的路径长度都比较短；

3.连接两个顶点之间的路径不会经过出度比较大的顶点。

假设要给用户u进行个性化推荐,可以从用户u对应的节点v,开始在用户物品二分图上进行随机游走。游走到任何一个节点时,首先按照概率α决定是继续游走,还是停止这次游走并从v,节点开始重新游走。如果决定继续游走,那么就从当前节点指向白的节点中按照均匀分布随机选择一个节点作为游走下次经过的节点。这样,经过很多次随机游走)后,每个物品节点被访问到的概率会收敛到一个数。最终的推荐列表中物品的权重就是物品节点的访问概率。描述成公式如下：

$PR(v)= \begin{cases} \alpha {\sum_{v'\in in(v)}{\frac{PR(v')}{|out(v')|}} }&\text{if } v \not =v_u \\ (1-\alpha)+\alpha \sum_{v'\in in(v)}{\frac{PR(v')}{|out(v')|}} &\text{if } v =v_u \end{cases}$

代码实现：

def PersonalRank(G, alpha, root, max_step): #G为图，alapha为用户继续浏览的概率，root为需要推荐的用户，max_step为迭代次数 rank = dict() rank = {x:0 for x in G.keys()} # 用0将G中的键对应的值全部替换，G不变 rank[root] = 1 #将rank中所有键为root的值全部换为1 #开始迭代 for k in range(max_step): tmp = {x:0 for x in G.keys()} #取节点i和它的出边尾节点集合ri for i, ri in G.items(): #取节点i的出边的尾节点j以及边E(i,j)的权重wij, 边的权重都为1，在这不起实际作用 for j, wij in ri.items(): #i是j的其中一条入边的首节点，因此需要遍历图找到j的入边的首节点， #这个遍历过程就是此处的2层for循环，一次遍历就是一次游走 tmp[j] += alpha * rank[i] / (1.0 * len(ri)) #我们每次游走都是从root节点出发，因此root节点的权重需要加上(1 - alpha) #在《推荐系统实践》上，作者把这一句放在for j, wij in ri.items()这个循环下，我认为是有问题。 tmp[root] += (1 - alpha) rank = tmp

免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/126043.html