LLC变换器等效分析

大家好，欢迎来到IT知识分享网。

如图2.3所示，当电路工作在在串联谐振频率， ，谐振电感Ls和串联谐振电容Cs发生串联谐振，a、b间等效为短路，此时无论Q值多小(即如多大)，b、c两点间并联电感Lp和负载Rac并联后都呈感性，所以从a、c点看入的入端阻抗都呈感性，谐振电路工作在我们所希望的感性状态下，该频率下，输出负载与增益无关。

如图2．4所示，当电路工作在，范围内时，a、b间呈感性，此时无论Q值多小(即如多大)，b、c两点间并联电感Lp和负载Rac并联后都呈感性，所以从a、c点看入的入端阻抗也都呈感性，所以在该频率下增益小于1，也就是降压模式。

如图2．5所示，当电路工作在，范围内时，a、b间呈容性，而b、c两点间仍然呈感性，所以a、c两点间阻抗到底是呈感性还是容性就要根据频率和负载轻重(即Q值大小)而定了。当负载一定时，工作频率越远离串联谐振频率，a、c间阻抗就越容易呈容性。工作频率越靠近串联谐振频率，a、c间阻抗就越容易呈感性。而当频率一定时，负载越大(Q值越大)，a、c间阻抗就越容易呈容性(增益下降)；负载越轻(Q值越小)，a、c间阻抗就越容易呈感性(增益变大)。

基于以上三种情况的分析，我们可以得到对某个负载(Q值恒定)而言，只要开关频率高于第一拐点频率(该频率点是Ls、Cs谐振频率点)，电路就工作在感性状态，容易实现开关MOS管的zvs。而这个拐点频率的物理意义也就是a、c间输入端阻抗Zin的阻性点；当开关频率刚好在拐点频率时谐振网络等效成一个电阻；当开关频率小于拐点频率时，谐振网络呈容性或感性，当开关频率小于第二拐点频率(Ls、Lp、Cs)时，谐振网络呈容性，当开关频率大于第二拐点频率而小于第一拐点频率时，谐振网络呈感性，

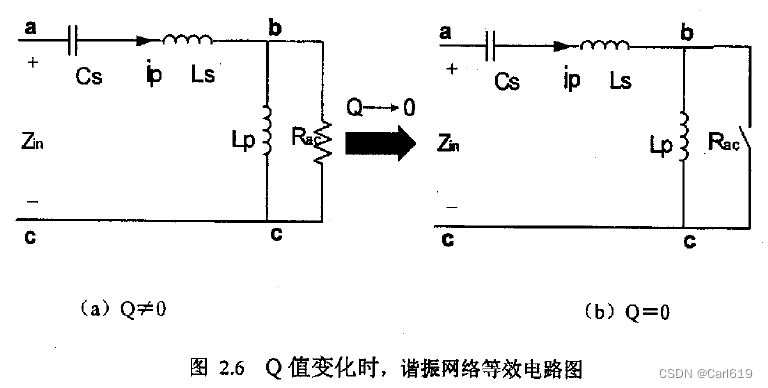
下面来解释一下为何无论Q值多小，第二拐点频率不会无限变小而趋近零，而是存在一个极限频率。其实这个极限频率就是电路的串并联谐振频率,原因是当串联谐振电感Ls、串联谐振电容Cs和并联电感Lp这些谐振元件参数都已经确定的情况下，Q值的不断减小，也就意味着负载不断变轻，直到变为空载状态，也就是负载Rac无限大，Q值趋近于零，连接负载的支路相当于开路，如图2．6所示。此时入端阻抗Zin的阻性点显然为Ls、Cs、Lp发生谐振的频率点。在这个频率点，a、c等效为短路。

我们希望LLC谐振变换器工作在范围内，这样能够有效地克服副边整流二极管的反向恢复损耗，而根据上文在图2．5中的等效，LLc谐振电路等效成了并联谐振电路，不过这种等效并联谐振电路又与传统的并联谐振电路不同，它们的电感电容位置是刚好相反的，LLc等效并联谐振电路中电容串在谐振槽路中，

电感与负载相并联；而在传统Lc并联谐振电路中电感串在谐振槽路中，电容与负载相并联。

LLc谐振变换器参数对变换器的影响

在LLc谐振变换器中最主要的参数有三个，分别是变压器匝比n、k=Lp/Ls 、

1. 固定匝比n和Q值，分析一下k值对变换器的影响。如图2．9所示，我们可以看到随着k值的增大，各条曲线在变缓，也就是最大增益(发生在处）在减小，预示着在输入电压较低时(增益最大)，变换器输出电压可能会无法调节到我们所想要保持恒定的值。从图中我们还可以发现随着k值的增大，增益曲线的拐点频率在减小，如果假定串联谐振频率已经确定，那就意味着变换器工作频率范围将会变宽，也就是说想要获得同样的瞬态响应，需要大范围的调节开关频率来进行稳定输出，这样以来，动态响应就变差了。

• 谐振电感Lr电容Cr一定，Lp增大，励磁电流减小，MOS管关断损耗减小，K值增大，增益曲线平坦，调频范围变宽，要考虑输出增益问题；
• 谐振电感Lr电容Cr一定，Lp减小，励磁电流增大，MOS管关断损耗增大，K值减小，增益曲线变陡，调频范围减小，要注意最低频率限制问题，容易进入容性区

1. 固定匝比n和k值，来分析一下Q值对变换器的影响。如图2.2所示，Q值的大小直接影响到变换器直流增益是否够大，在输入电压较低时输出电压能否达到我们所需的值。而如果串联谐振频率一定时，如果Q值越小则拐点频率(即串并联谐振频率)就越小，这样开关频率变化范围就会相应增大。

1. 固定k和Q值

在串联谐振频率点时，不论Q值多少，所有的增益曲线都过同一点，即Q值不影响变换器增益在串联谐振频率点时为1/2n,所以当匝比的设计刚好能满足变换器的最小增益为1/2n时，变换器将全范围工作在我们想让变换器工作在，而如果匝比的设计使得1/2n大于变换器的最小增益时，变换器将有一部分时间工作在的区间内，这时变换器就无法保证克服副边整流二极管的反向恢复损耗；而如果匝比的设计使得1/2n小于变换器的最小增益时，变换器将全范围工作在的区间内。且n越大，变换器的工作区域就越远离串联谐振频率上。而在n增大的过程中．并联电感Lp上的钳位电压也在增大，这样在k值不变的情况下，并联电感上的损耗将会增加。