大家好,欢迎来到IT知识分享网。
本文介绍如何从大地坐标(纬度、经度和椭球上方高度)转换为地心、地球固定坐标,然后再转换回来。该算法是封闭形式的(即非迭代的)、快速且高度准确。示例代码以 Java 形式提供。
1、大地坐标的定义
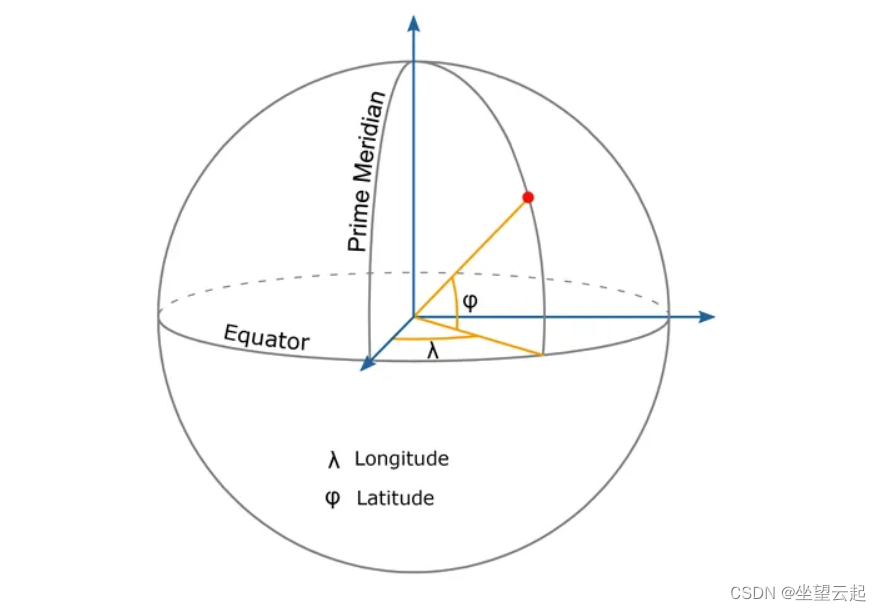
大地测量系统使用极坐标,定义如下:
| 纬度: | 赤道以北和以南的角度。正角位于北半球,负角位于南半球。角度范围为 -90 度(-π/2 弧度)至 +90 度(+π/2 弧度)。赤道上的点的纬度为零。 |
| 经度: | 本初子午线以东和以西的角度。本初子午线是一条穿过英国格林威治的南北线。正经度位于本初子午线以东,负角度位于本初子午线以西。角度范围为 -180 度(-π 弧度)至 +180 度(+π 弧度)。 |
| 高度: | 也称为高度或海拔,表示地球椭球体上方的高度,以米为单位。地球椭球体是由长半轴和短半轴定义的数学表面。这两个参数最常见的值由 1984 年世界大地测量标准 (WGS-84) 定义。WGS-84 椭球体旨在与平均海平面相对应,但实际上,由于洋流、科里奥利效应和地球引力场的局部变化,实际平均海平面在世界各地有所不同。因此,大地测量高度为零大致对应于海平面,正值随着远离地球中心而增加。高度值的理论范围是从地球中心(约-6,371公里)到正无穷大。然而,在实践中,很少使用更深于几公里或高于地球同步轨道(约 36,000 公里)的高度值。 |
2、地心地固 (ECEF) 坐标的定义
ECEF 是一个右手笛卡尔坐标系,原点位于地球中心,并且相对于地球固定(即随地球旋转)。单位为米。三个轴定义如下:
| X: | 在本初子午线穿过赤道(纬度 = 0,经度 = 0)。 |
| Y: | 通过本初子午线以东 90 度的赤道(纬度 = 0,经度 = 90 度)。 |
| Z: | 穿过北极(纬度 = 90 度,经度 = 任意值)。 |
3、坐标转换
这两种坐标系都有优点和缺点。大地测量系统用于导航、地图绘制和 GPS 应用,其三个组成部分可以直观地解释为分别代表北/南、东/西和上/下运动。另一方面,ECEF系统对于涉及欧几里得几何和旋转矩阵的计算更方便。因此,经常需要在两个系统之间来回转换。
事实上,从 Geodetic 到 ECEF 的转换相对简单,只涉及少量计算。然而,逆运算则更加困难。在过去的几年里,从 ECEF 转换到 Geodetic 需要迭代算法。1994年,北京大学的朱继杰发表了第一个封闭式解决方案。从那时起,已经开发了几种替代的封闭式解决方案,每种解决方案都有其优点和缺点。下面给出的解决方案是由当时在美国海军空战中心的 Donald K. Olson 开发的(Olson, DK (1996))。“将地心固定坐标转换为大地坐标”, IEEE 航空航天和电子系统汇刊,第 32 卷,第 1 期,1996 年 1 月,第 473-476 页)。
(1)示例代码
下面显示了 Olson 的 ECEF-to-Geodetic 算法的 Java 方法以及标准 Geodetic-to-ECEF 算法。前两个类变量(a和e2)定义 WGS-84 椭球体,其中a是长半轴(地球赤道处的半径),e2是偏心率的平方。其余常量可以从注释中记录的前两个常量导出,这样做不会降低准确性或增加计算时间。
public class Coord { private static final double a = .0; //WGS-84 semi-major axis private static final double e2 = 6.77997e-3; //WGS-84 first eccentricity squared private static final double a1 = 4.57535e+4; //a1 = a*e2 private static final double a2 = 1.75455e+9; //a2 = a1*a1 private static final double a3 = 1.12413e+2; //a3 = a1*e2/2 private static final double a4 = 4.88637e+9; //a4 = 2.5*a2 private static final double a5 = 4.55659e+4; //a5 = a1+a3 private static final double a6 = 9.86220e-1; //a6 = 1-e2 private static double zp,w2,w,r2,r,s2,c2,s,c,ss; private static double g,rg,rf,u,v,m,f,p,x,y,z; private static double n,lat,lon,alt; //Convert Earth-Centered-Earth-Fixed (ECEF) to lat, Lon, Altitude //Input is a three element array containing x, y, z in meters //Returned array contains lat and lon in radians, and altitude in meters public static double[] ecef_to_geo( double[] ecef ){ double[] geo = new double[3]; //Results go here (Lat, Lon, Altitude) x = ecef[0]; y = ecef[1]; z = ecef[2]; zp = Math.abs( z ); w2 = x*x + y*y; w = Math.sqrt( w2 ); r2 = w2 + z*z; r = Math.sqrt( r2 ); geo[1] = Math.atan2( y, x ); //Lon (final) s2 = z*z/r2; c2 = w2/r2; u = a2/r; v = a3 - a4/r; if( c2 > 0.3 ){ s = ( zp/r )*( 1.0 + c2*( a1 + u + s2*v )/r ); geo[0] = Math.asin( s ); //Lat ss = s*s; c = Math.sqrt( 1.0 - ss ); } else{ c = ( w/r )*( 1.0 - s2*( a5 - u - c2*v )/r ); geo[0] = Math.acos( c ); //Lat ss = 1.0 - c*c; s = Math.sqrt( ss ); } g = 1.0 - e2*ss; rg = a/Math.sqrt( g ); rf = a6*rg; u = w - rg*c; v = zp - rf*s; f = c*u + s*v; m = c*v - s*u; p = m/( rf/g + f ); geo[0] = geo[0] + p; //Lat geo[2] = f + m*p/2.0; //Altitude if( z < 0.0 ){ geo[0] *= -1.0; //Lat } return( geo ); //Return Lat, Lon, Altitude in that order } //Convert Lat, Lon, Altitude to Earth-Centered-Earth-Fixed (ECEF) //Input is a three element array containing lat, lon (rads) and alt (m) //Returned array contains x, y, z in meters public static double[] geo_to_ecef( double[] geo ) { double[] ecef = new double[3]; //Results go here (x, y, z) lat = geo[0]; lon = geo[1]; alt = geo[2]; n = a/Math.sqrt( 1 - e2*Math.sin( lat )*Math.sin( lat ) ); ecef[0] = ( n + alt )*Math.cos( lat )*Math.cos( lon ); //ECEF x ecef[1] = ( n + alt )*Math.cos( lat )*Math.sin( lon ); //ECEF y ecef[2] = ( n*(1 - e2 ) + alt )*Math.sin( lat ); //ECEF z return( ecef ); //Return x, y, z in ECEF } }(2)准确性
奥尔森的算法计算成本低,并且与某些解决方案不同,不需要在极地或赤道进行特殊处理。它也非常准确。Olson 在他的原始论文中运行了大量的点,定期在纬度和经度上进行采样,并计算每个点的 3D 误差(以米为单位)。在-10公里和+100公里之间的高度,他发现平均误差为



使用上面所示的代码进行的测试中,从纬度、经度和海拔的随机均匀分布中生成了 1 亿个点,海拔限制在 -1000 公里到 +100,000 公里的范围内。我们生成大地坐标(lat、lon、alt)中的点,将它们转换为 ECEF,然后返回大地坐标。然后我们将原始大地坐标与双重转换的结果进行比较。
对于纬度和经度测量,任何点的最大误差为 


免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/127455.html