基本频谱分析

大家好，欢迎来到IT知识分享网。

一、基本频谱分析

傅里叶变换是用于对时域信号执行频率和功率谱分析的工具。

频谱分析数量

频谱分析研究非均匀采样的离散数据中包含的频谱。傅里叶变换是通过在频率空间表示基于时间或空间的信号来揭示该信号的频率分量的工具。下表列出了用于描述和解释信号属性的常用量。要了解有关傅里叶变换的更多信息，请参阅傅里叶变换。

含噪信号

傅里叶变换可以计算被随机噪声破坏的信号的频率分量。

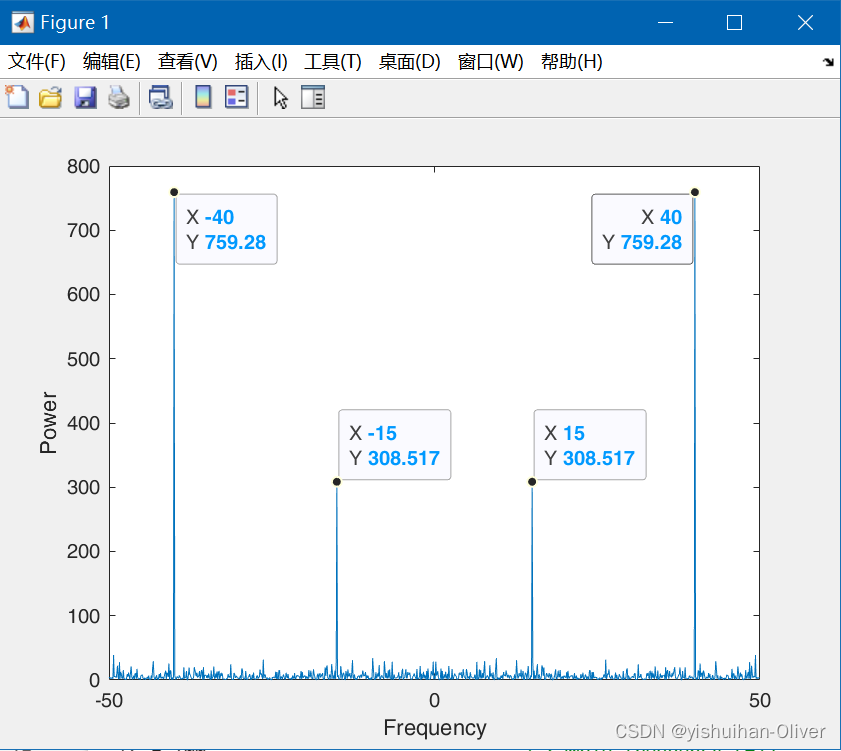
创建具有 15 Hz 和 40 Hz 分量频率的信号，并插入随机高斯噪声。

rng('default') fs = 100; % sample frequency (Hz) t = 0:1/fs:10-1/fs; % 10 second span time vector x = (1.3)*sin(2*pi*15*t) ... % 15 Hz component + (1.7)*sin(2*pi*40*(t-2)) ... % 40 Hz component + 2.5*randn(size(t)); % Gaussian noise;

信号的傅里叶变换可确定其频率分量。在 MATLAB® 中，fft 函数使用快速傅里叶变换算法计算傅里叶变换。使用 fft 计算信号的离散傅里叶变换。

y = fft(x); % FFT变换

将功率谱绘制为频率的函数。尽管噪声在基于时间的空间内伪装成信号的频率分量，但傅里叶变换将其显现为功率尖峰。

n = length(x); % number of samples f = (0:n-1)*(fs/n); % frequency range power = abs(y).^2/n; % power of the DFT plot(f,power) xlabel('Frequency') ylabel('Power') 

在许多应用中，查看以 0 频率为中心的功率谱更加方便，因为它能更好地显示信号的周期性。使用 fftshift 函数对 y 执行循环平移，并绘制以 0 为中心的功率。

y0 = fftshift(y); % shift y values f0 = (-n/2:n/2-1)*(fs/n); % 0-centered frequency range power0 = abs(y0).^2/n; % 0-centered power plot(f0,power0) xlabel('Frequency') ylabel('Power')

音频信号

您可以使用傅里叶变换来分析音频数据的频谱。

文件 bluewhale.au 包含水下麦克风记录的加利福尼亚海岸的太平洋蓝鲸发声的音频数据。此文件来自于康奈尔大学生物声学研究项目保存的动物发声库。

由于蓝鲸的叫声频率如此之低，以至人类几乎听不到。数据中的时间标度压缩了 10 倍，以便提高音调并使叫声更清晰可闻。读取并绘制音频数据。可使用命令 sound(x,fs) 来收听音频。

whaleFile = 'bluewhale.au'; [x,fs] = audioread(whaleFile); plot(x) xlabel('Sample Number') ylabel('Amplitude')

第一个声音为“颤音”，之后是三个“呻吟音”。本示例将分析单个呻吟音。指定大致包含第一个呻吟音的新数据，并校正时间数据以体现 10 部的加速。将截断的信号绘制为时间的函数。

moan = x(2.45e4:3.10e4); t = 10*(0:1/fs:(length(moan)-1)/fs); plot(t,moan) xlabel('Time (seconds)') ylabel('Amplitude') xlim([0 t(end)])

数据的傅里叶变换确定了音频信号的频率分量。在一些使用 fft 处理大量数据的应用中，通常需要调整输入，使样本数量为 2 的幂。这样可以大幅提高变换计算的速度，对于具有较大质因数的样本大小更是如此。指定新的信号长度 n（2 的幂），并使用 fft 函数计算信号的离散傅里叶变换。fft 会自动使用零来填充原始数据，以增加样本大小。

m = length(moan); % original sample length n = pow2(nextpow2(m)); % transform length y = fft(moan,n); % DFT of signal

根据加速因子调整频率范围，并计算和绘制信号的功率谱。绘图指示，呻吟音包含约 17 Hz 的基本频率和一系列谐波（其中强调了第二个谐波）。

f = (0:n-1)*(fs/n)/10; power = abs(y).^2/n; plot(f(1:floor(n/2)),power(1:floor(n/2))) xlabel('Frequency') ylabel('Power')

另请参阅

fft | fftshift | nextpow2 | ifft | fft2 | fftn

相关主题

• 傅里叶变换
• 二维傅里叶变换

二、使用 FFT 进行频谱分析

       下面的示例说明了如何使用 FFT 函数进行频谱分析。FFT 的一个常用场景是确定一个时域含噪信号的频率分量。

       首先创建一些数据。假设是以 1000 Hz 的频率对数据进行的采样。首先为数据构造一条时间轴，时间范围从 t = 0 至 t = 0.25，步长为 1 毫秒。然后，创建一个包含 50 Hz 和 120 Hz 频率的正弦波信号 x。

fs = 1000; t = 0:.001:.25; x = sin(2*pi*50*t) + sin(2*pi*120*t);

添加一些标准差为 2 的随机噪声以产生含噪信号 y。然后，通过对该含噪信号 y 绘图来了解该信号。

y = x + 2*randn(size(t)); plot(y(1:50)) title('Noisy time domain signal')

很明显，通过观察该信号很难确定频率分量；这就是频谱分析为什么被广泛应用的原因。

得到含噪信号 y 的离散傅里叶变换很容易；执行快速傅里叶变换 (FFT) 即可实现。

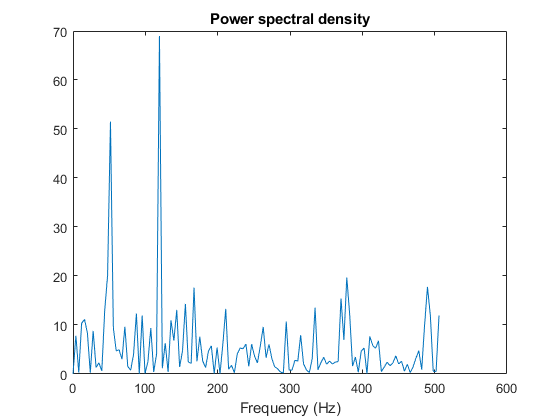
Y = fft(y,256);

使用复共轭 (CONJ) 计算功率谱密度，即测量不同频率下的能量。为前 127 个点构造一个频率轴，并使用该轴绘制结果图形。（其余的点是对称的。）

Pyy = Y.*conj(Y)/256; f = 1000/256*(0:127); plot(f,Pyy(1:128)) title('Power spectral density') xlabel('Frequency (Hz)')

放大并仅绘制上限为 200 Hz 的图形。请注意 50 Hz 和 120 Hz 下的峰值。以下是原始信号的频率。

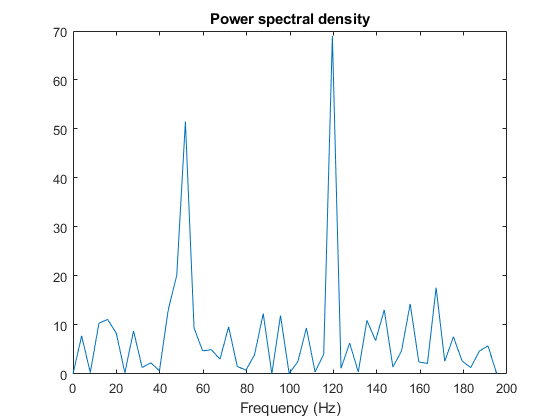
plot(f(1:50),Pyy(1:50)) title('Power spectral density') xlabel('Frequency (Hz)')

%% Fs = 1000; % Sampling frequency T = 1/Fs; % Sampling period L = 1500; % Length of signal t = (0:L-1)*T; % Time vector %50Hz和120Hz频率信号 S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); %添加随机噪声 X = S + 2*randn(size(t)); figure; plot(1000*t(1:50), X(1:50)) title('Signal Corrupted with Zero-Mean Random Noise') xlabel('t (milliseconds)') ylabel('X(t)') set(gca,'Fontname','Monospaced'); %加噪声后信号X长度1500，进行1500点FFT Y = fft(X); %为何除以信号长度L? P2 = abs(Y/L); P1 = P2(1:L/2+1);%单边谱 P1(2:end-1) = 2*P1(2:end-1);%由于P1(1)是直流. f = Fs*(0:(L/2))/L;%采样频率Fs,因此只看fs/2内的信号 figure;plot(f,P1) title('Single-Sided Amplitude Spectrum of X(t)') xlabel('f (Hz)') ylabel('|P1(f)|') set(gca,'Fontname','Monospaced'); %原始信号S长度1500，进行1500点FFT Y = fft(S); P2 = abs(Y/L); P1 = P2(1:L/2+1); P1(2:end-1) = 2*P1(2:end-1); figure;plot(f,P1) title('Single-Sided Amplitude Spectrum of S(t)') xlabel('f (Hz)') ylabel('|P1(f)|') set(gca,'Fontname','Monospaced');

【注意】：

1、FFT 之后信号幅度值变大，要得到真实幅度值大小，要将变换后结果除以N再乘以2（直流即零频率处除以N），除以N得到双边频谱，乘以2得到单边频谱。如果原始信号就是复数信号，则FFT得到的就是单边频谱不用乘以2。

2、对 fs采样频率信号，FFT之后最高频率为采样频率一半，FFT之后的值关于半采样率共轭对称。