麦克纳姆轮系运动学模型解算与分析

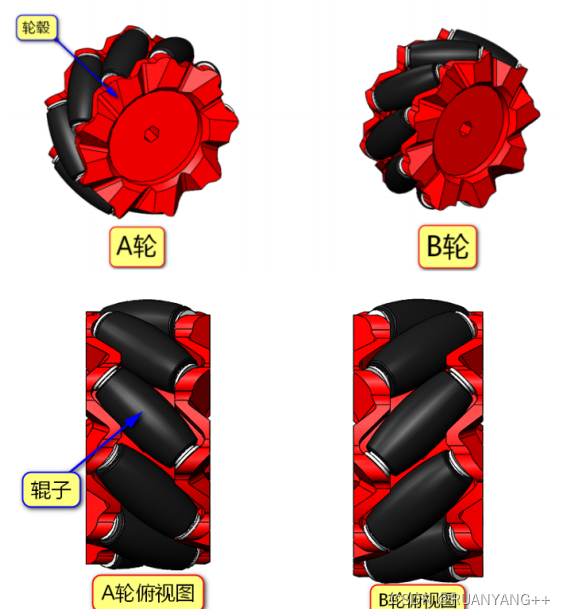
麦克纳姆轮是一种可全方位移动的全向轮，由轮毂和围绕轮毂的辊子组成，麦轮辊子轴线和轮毂轴线夹角成45°。在轮毂的轮缘上斜向分布着许多小轮子，即辊子，辊子是一种没有动力的从动小滚轮。这种全方位移动方式是基于一个有许多位于机轮周边的轮轴的中心轮的原理上，这些成角度的周边轮轴把一部分的机轮转向力转化到一个机轮法向力上面。麦克纳姆轮分为两种类型，这两种类型的麦轮互为镜像关系大的A、B两种，或者被称为左旋轮和右旋轮。这一般会在轮毂上面有标识A和B、L和R。

二.麦轮的安装方法

麦轮一般是四个一组使用，两个左旋轮，两个右旋轮。左旋轮和右旋轮呈手性对称。

安装方式有多种，主要分为：X-正方形（X-square）、X-长方形（X-rectangle）、O-正方形（O-square）、O-长方形（O-rectangle）。其中 X 和 O 表示的是与四个轮子地面接触的辊子所形成的图形；正方形与长方形指的是四个轮子与地面接触点所围成的形状。

X-正方形：轮子转动产生的力矩会经过同一个点，所以 yaw 轴无法主动旋转，也无法主动保持 yaw 轴的角度。一般几乎不会使用这种安装方式。
X-长方形：轮子转动可以产生 yaw 轴转动力矩，但转动力矩的力臂一般会比较短。这种安装方式也不多见。
O-正方形：四个轮子位于正方形的四个顶点，平移和旋转都没有任何问题。受限于机器人底盘的形状、尺寸等因素，这种安装方式虽然理想，但可遇而不可求。
O-长方形：轮子转动可以产生 yaw 轴转动力矩，而且转动力矩的力臂也比较长。是最常见的安装方式。

三.麦轮正逆运动学模型

以O-长方形的安装方式为例，四个轮子的着地点形成一个矩形。正运动学模型（forward kinematic model）将得到一系列公式，让我们可以通过四个轮子的速度，计算出底盘的运动状态；而逆运动学模型（inverse kinematic model）得到的公式则是可以根据底盘的运动状态解算出四个轮子的速度。需要注意的是，底盘的运动可以用三个独立变量来描述：X轴平动、Y轴平动、yaw 轴自转；而四个麦轮的速度也是由四个独立的电机提供的。所以四个麦轮的合理速度是存在某种约束关系的，逆运动学可以得到唯一解，而正运动学中不符合这个约束关系的方程将无解。

先试图构建逆运动学模型，由于麦轮底盘的数学模型比较复杂，我们在此分四步进行：

1.将底盘的运动分解为三个独立变量来描述；

2.根据第一步的结果，计算出每个轮子轴心位置的速度；

3.根据第二步的结果，计算出每个轮子与地面接触的辊子的速度；

4.根据第三部的结果，计算出轮子的真实转速。

3.1 底盘运动的分解

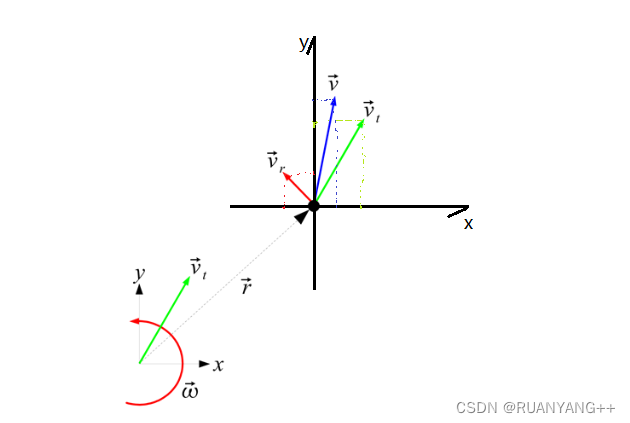
我们知道，刚体在平面内的运动可以分解为三个独立分量：X轴平动、Y轴平动、yaw 轴自转。如下图所示，底盘的运动也可以分解为三个量：

$_{}$ $v_{tx}$ 表示 X 轴运动的速度，即左右方向，定义向右为正；

$v_{ty}$ 表示 Y 轴运动的速度，即前后方向，定义向前为正；

$\vec{\omega }$ 表示 yaw 轴自转的角速度，定义逆时针为正。

以上三个量一般都视为四个轮子的几何中心（矩形的对角线交点）的速度。

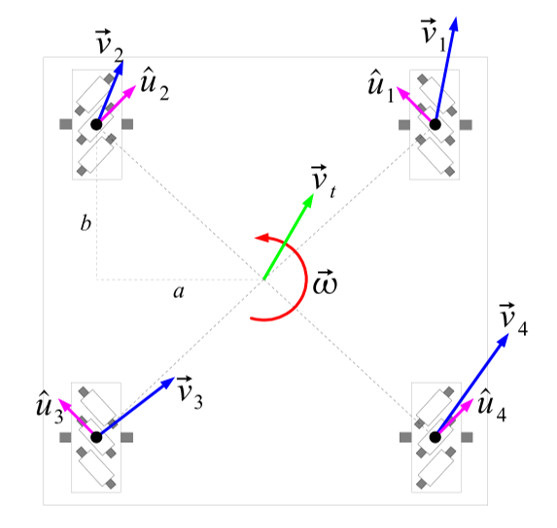
3.2 计算出轮子轴心位置的速度

定义：

$\vec{r}$ 为从几何中心指向轮子轴心的矢量；

$\vec{v}$ 为轮子轴心的运动速度矢量；

$\vec{v_{r}}$ 为轮子轴心沿垂直于 $\vec{r}$ 的方向（即切线方向）的速度分量；

那么可以计算出：

$\vec{v}= \vec{v_{t}}+\vec{v_{r}}=\vec{v_{t}}+\vec{\omega }\times \vec{r}$

分别计算矢量 $\vec{v}$ 的 X、Y 轴的分量
$\left\{\begin{matrix}v_{x}=v _{tx}-\omega \cdot r_{y} & \\ v_{y}=v _{ty}+\omega \cdot r_{x} & \end{matrix}\right.$

同理可以算出其他三个轮子轴心的速度。

3.3 计算辊子的速度

根据轮子轴心的速度，可以分解出沿辊子方向的速度 $\vec{v_{\parallel }}$ 和垂直于辊子方向的速度 $\vec{v_{\perp }}$ 。其中 $\vec{v_{\perp }}$ 是可以无视的（思考题：为什么垂直方向的速度可以无视？），而

$\vec{v_{\parallel }}= \vec{v}\cdot \vec{u}= \left ( v_{x} \hat{i} +v_{y}\hat{j}\right )\left ( -\frac{1}{\sqrt{2}}\hat{i} +\frac{1}{\sqrt{2}}\hat{j}\right )=\frac{1}{\sqrt{2}}v_{x}+\frac{1}{\sqrt{2}}v_{y}$

其中 $\vec{u}$ 是沿辊子方向的单位矢量。

3.4 计算轮子的速度

从辊子速度到轮子转速的计算比较简单：

$v_{x}=\frac{v_{\parallel }}{\cos 45}= \sqrt{2}\left (-\frac{1}{\sqrt{2}}v_{x} + -\frac{1}{\sqrt{2}}v_{y}\right )=-v_{x}+v_{y}$

根据上图所示的和的定义，有

$\left\{\begin{matrix}v_{x}=v_{tx}+\omega b & & \\ v_{y}=v_{ty}-\omega a & & \end{matrix}\right.$

结合以上四个步骤，可以根据底盘运动状态解算出四个轮子的转速：

$\left\{\begin{matrix}v_{\omega 1}=v_{ty}-v_{tx}+\omega (a+b)) & \\v_{\omega 2}=v_{ty}+v_{tx}-\omega (a+b)) & \\ v_{\omega 3}=v_{ty}-v_{tx}-\omega (a+b)) & \\ v_{\omega 4}=v_{ty}+v_{tx}+\omega (a+b)) & \end{matrix}\right.$

以上方程组就是O-长方形麦轮底盘的逆运动学模型，而正运动学模型可以直接根据逆运动学模型中的三个方程解出来，此处不再赘述。

另一种计算方式

「传统」的推导过程虽然严谨，但还是比较繁琐的。这里介绍一种简单的逆运动学计算方式。

我们知道，全向移动底盘是一个纯线性系统，而刚体运动又可以线性分解为三个分量。那么只需要计算出麦轮底盘在「沿X轴平移」、「沿Y轴平移」、「绕几何中心自转」时，四个轮子的速度，就可以通过简单的加法，计算出这三种简单运动所合成的「平动+旋转」运动时所需要的四个轮子的转速。而这三种简单运动时，四个轮子的速度可以通过简单的测试，或是推动底盘观察现象得出。

当底盘沿着 X 轴平移时：

$\left\{\begin{matrix}v_{\omega 1}=-v_{tx} & \\ v_{\omega 2}=+v_{tx} & \\ v_{\omega 3}=-v_{tx} & \\ v_{\omega 4}=+v_{tx} & \end{matrix}\right.$

当底盘沿着 Y 轴平移时：

$\left\{\begin{matrix}v_{\omega 1}=v_{ty} & \\ v_{\omega 2}=v_{ty} & \\ v_{\omega 3}=v_{ty} & \\ v_{\omega 4}=v_{ty} & \end{matrix}\right.$

当底盘绕几何中心自转时：

$\left\{\begin{matrix}v_{\omega 1}=+\omega(a+b) & \\ v_{\omega 2}=-\omega(a+b) & \\ v_{\omega 3}=-\omega(a+b) & \\ v_{\omega 4}=+\omega(a+b) & \end{matrix}\right.$

将以上三个方程组相加，得到的恰好是根据「传统」方法计算出的结果。这种计算方式不仅适用于O-长方形的麦轮底盘，也适用于任何一种全向移动的机器人底盘。

四.麦轮的运动分析

4.1 两种类型麦轮运动分析

对于A轮，如果A轮向前运动时同时向右运动，即斜向右前方运动，那么相反，A轮向后运动的同时会向左运动，即斜向左后方运动；

对于A轮，如果A轮向前运动时同时向左运动，即斜向左前方运动，那么相反，A轮向后运动的同时会向右运动，即斜向右后方运动；

4.2 麦轮车整体运动分析

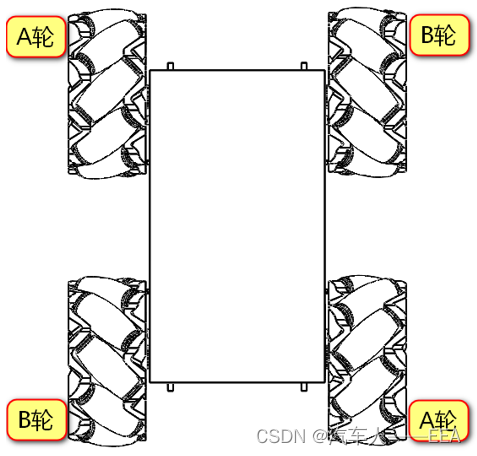
以O-长方形安装为例（最常见的安装方法）

A轮（左旋）与B轮（右旋）互为镜像关系

麦轮在车上的分布：（“外八”，AB对角安装）

地面投影：（“内八”）

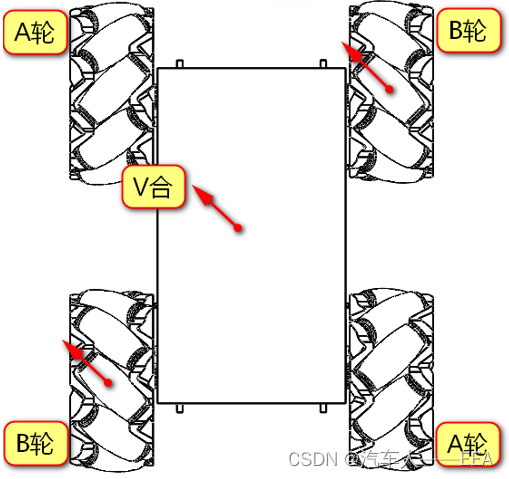
1.前进：（AB轮可以相互抵消轴向速度，正转：沿辊子轴向上；反转：沿辊子轴向下）

2.倒退：（AB轮可以相互抵消轴向速度）

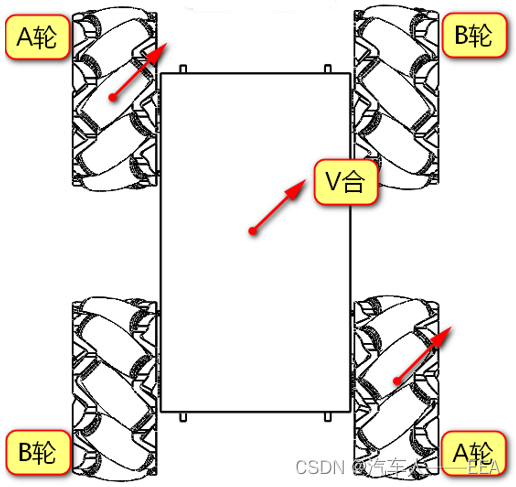
3.左移：（A轮反转，B轮正转）

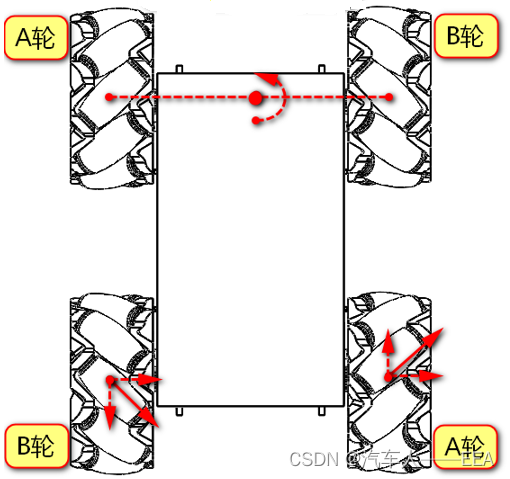
4.原地左转掉头：（左前：反转；右前正转；左后：反转；右后：正转。即同侧左：反转；同侧右：正转）

5.原地右转掉头：（左前：正转；右前反转；左后：正转；右后：反转。即同侧左：正转；同侧右：反转）

6.左前（对角B轮：正转，对角A轮：不转）

7.右前（对角A轮：正转，对角B轮：不转）

8.左后（对角A轮：反转，对角B轮：不转）

9.右后 （对角B轮：反转，对角A轮：不转）

10.绕前轴中心左转（前轴A、B轮：不转；后轴B轮：反转，A轮：正转）

11.绕前轴中心右转 （前轴A、B轮：不转；后轴B轮：正转，A轮：反转）

12.绕后轴中心左转（后轴A、B轮：不转；前轴B轮：正转，A轮：反转）

13.绕后轴中心右转（后轴A、B轮：不转；前轴B轮：反转，A轮：正转）

运动方向	左前——A轮	右前——B轮	左后——B轮	右后——A轮
前进	正转	正转	正转	正转
倒退	反转	反转	反转	反转
左移	反转	正转	正转	反转
右移	正转	反转	反转	正转
原地左转掉头	反转	正转	反转	正转
原地右转掉头	正转	反转	正转	反转
左前	不转	正转	正转	不转
右前	正转	不转	不转	正转
左后	反转	不转	不转	反转
右后	不转	反转	反转	不转
绕前轴中心左转	不转	不转	反转	正转
绕前轴中心右转	不转	不转	正转	反转
绕后轴中心左转	反转	正转	不转	不转
绕后轴中心右转	正转	反转	不转	不转

五.麦轮控制实现

5.1 麦轮简单控制

这里简单控制指的是只控制麦轮小车的方向，实现麦轮小车的前进、后退，平移等，而并不关心麦轮小车的速度，那么我们只需要根据麦轮小车运动公式进行赋值就ok了。

主控：STM32
开发平台：KEIL5

/ * @brief 设置小车速度 * @param linear_Pwm_x x方向PWM值 * @param linear_Pwm_y y方向PWM值 * @param angular_Pwm_z z轴角速度PWM值 */ void Set_Pwm_Vel(int linear_Pwm_x, int linear_Pwm_y, int angular_Pwm_z) { Car_AHL_Pwm = linear_Pwm_y - linear_Pwm_x + angular_Pwm_z*(a+b); Car_AHR_Pwm = linear_Pwm_y + linear_Pwm_x - angular_Pwm_z*(a+b); Car_AFL_Pwm = linear_Pwm_y - linear_Pwm_x - angular_Pwm_z*(a+b); Car_AFL_Pwm = linear_Pwm_y + linear_Pwm_x + angular_Pwm_z*(a+b); TIM1->CCR1 = Car_AHL_Pwm; TIM1->CCR2 = Car_AHR_Pwm; TIM1->CCR3 = Car_AFL_Pwm; TIM1->CCR4 = Car_AFL_Pwm; }

我们通过设置x轴、y轴、z轴的PWM值来控制小车的方向，PWM的数值要根据定时器的ARR值进行调节，通过调节PWM值，可以大概的控制小车的速度，这样简单的完成了麦轮小车控制，但是这种控制方式会导致小车速度不稳定不可控，需要反复调节，方向也无法做到精确控制，这里不推荐这种控制方法。

5.2 麦轮小车的精确控制

这里所说的精确控制指的是既控制小车的方向又控制小车的速度，所以这里我们需要用到PID控制算法了，通过PID算法来控制每个轮子的速度，从而控制小车整体的速度。

主控：STM32
开发平台：KEIL5

1.设置小车速度

/ * @brief 设置小车速度 * @param linear_x x方向线速度 * @param linear_y y方向线速度 * @param angular_z z轴角速度 */ void Set_Vel(float linear_x, float linear_y, float angular_z) { kinematics.exp_vel.linear_x = linear_x; kinematics.exp_vel.linear_y = linear_y; kinematics.exp_vel.angular_z = angular_z; }//设置期望速度

2.计算期望速度

void Exp_Speed_Cal(u32 dT_us) { float linear_vel_x_mins; float linear_vel_y_mins; float angular_vel_z_mins; float tangential_vel; float x_rpm; float y_rpm; float tan_rpm; // 将 m/s 转换为 m/min linear_vel_x_mins = kinematics.exp_vel.linear_x * 60.0f; linear_vel_y_mins = kinematics.exp_vel.linear_y * 60.0f; // 将 rad/s 转换为 rad/min angular_vel_z_mins = kinematics.exp_vel.angular_z * 60.0f; // 切向速度 tangential_vel = angular_vel_z_mins * ((kinematics.wheels_x_distance_ / 2) + (kinematics.wheels_y_distance_ / 2)); x_rpm = linear_vel_x_mins / kinematics.wheel_circumference_; y_rpm = linear_vel_y_mins / kinematics.wheel_circumference_; // tan_rpm = tangential_vel / kinematics.wheel_circumference_; // 当用姿态传感器测量得到的z轴角速度和用编码器数据解算得到的角速度相差很大时， // 可认为轮子打滑 if((kinematics.exp_vel.linear_x == 0 && kinematics.exp_vel.linear_y == 0 && kinematics.exp_vel.angular_z == 0) || my_abs(sensor.gyro_rps[Z] - kinematics.fb_vel.angular_z) > 0.5) { pid_yaw.out = tangential_vel / kinematics.wheel_circumference_; } else { PID_Controller( dT_us, // 控制周期 us kinematics.exp_vel.angular_z, // 目标值 sensor.gyro_rps[Z], // 反馈值 &pid_yaw,// PID参数 0,// 单次积分限幅 0); // 积分限幅 // 输出限幅 pid_yaw.out = Get_MiMx( pid_yaw.out, -kinematics.max_rpm_, kinematics.max_rpm_); } tan_rpm = pid_yaw.out; // 使用逆运动学模型计算车轮的期望速度 // 左前轮电机 kinematics.exp_wheel_rpm.motor_1 = x_rpm - y_rpm - tan_rpm; kinematics.exp_wheel_rpm.motor_1 = Get_MiMx(kinematics.exp_wheel_rpm.motor_1, -kinematics.max_rpm_, kinematics.max_rpm_); // 右前轮电机 kinematics.exp_wheel_rpm.motor_2 = x_rpm + y_rpm + tan_rpm; kinematics.exp_wheel_rpm.motor_2 = Get_MiMx(kinematics.exp_wheel_rpm.motor_2, -kinematics.max_rpm_, kinematics.max_rpm_); // 左后轮电机 kinematics.exp_wheel_rpm.motor_3 = x_rpm + y_rpm - tan_rpm; kinematics.exp_wheel_rpm.motor_3 = Get_MiMx(kinematics.exp_wheel_rpm.motor_3, -kinematics.max_rpm_, kinematics.max_rpm_); // 右后轮电机 kinematics.exp_wheel_rpm.motor_4 = x_rpm - y_rpm + tan_rpm; kinematics.exp_wheel_rpm.motor_4 = Get_MiMx(kinematics.exp_wheel_rpm.motor_4, -kinematics.max_rpm_, kinematics.max_rpm_); }

3.测量实际速度

void Encoder_Task(u32 dT_us) { curr_encoder[0] = -(short)TIM2->CNT; // FL 1 curr_encoder[1] = (short)TIM3->CNT; // FR 2 curr_encoder[2] = -(short)TIM4->CNT; // BL 3 curr_encoder[3] = (short)TIM20->CNT; // BR 4 for(int i = 0; i < 4; i++){ encoder_incre[i] = curr_encoder[i] - last_encoder[i]; if(encoder_incre[i] > 10000){ encoder_incre[i] -= 65535; } else if(encoder_incre[i] < -10000){ encoder_incre[i] += 65535; } last_encoder[i] = curr_encoder[i]; } // printf("enc: %d %d %d %d\r\n", curr_encoder[0], curr_encoder[1], curr_encoder[2], curr_encoder[3]); // printf("inc: %d %d %d %d\r\n", encoder_incre[0], encoder_incre[1], encoder_incre[2], encoder_incre[3]); float dT_s = dT_us * 1e-6; kinematics.fb_wheel_rpm.motor_1 = encoder_incre[0] / 30000.0f / dT_s * 60.0f; kinematics.fb_wheel_rpm.motor_2 = encoder_incre[1] / 30000.0f / dT_s * 60.0f; kinematics.fb_wheel_rpm.motor_3 = encoder_incre[2] / 30000.0f / dT_s * 60.0f; kinematics.fb_wheel_rpm.motor_4 = encoder_incre[3] / 30000.0f / dT_s * 60.0f; }

4.电机整体控制

void Motor_Task(u32 dT_us) { Encoder_Task(dT_us); // 获取编码器读数 Exp_Speed_Cal(dT_us); // 计算期望速度 Fb_Speed_Cal(dT_us); // 计算反馈速度 // 左前轮PID控制 PID_Controller( dT_us,// 控制周期 kinematics.exp_wheel_rpm.motor_1, // 期望值 kinematics.fb_wheel_rpm.motor_1, // 反馈值 &pid[FL], // PID参数 0,// 单次积分限幅 0); // 积分限幅 pid[FL].out = Get_MiMx(pid[FL].out, -1.0, 1.0); // 输出限幅 // 右前轮PID控制 PID_Controller( dT_us, // 控制周期 kinematics.exp_wheel_rpm.motor_2, // 期望值 kinematics.fb_wheel_rpm.motor_2, // 反馈值 &pid[FR],// PID参数 0,// 单次积分限幅 0); // 积分限幅 pid[FR].out = Get_MiMx(pid[FR].out, -1.0, 1.0); // 输出限幅 // 左后轮PID控制 PID_Controller( dT_us,// 控制周期 kinematics.exp_wheel_rpm.motor_3, // 期望值 kinematics.fb_wheel_rpm.motor_3, // 反馈值 &pid[BL],// PID参数 0,// 单次积分限幅 0); // 积分限幅 pid[BL].out = Get_MiMx(pid[BL].out, -1.0, 1.0); // 输出限幅 // 右后轮PID控制 PID_Controller( dT_us, // 控制周期 kinematics.exp_wheel_rpm.motor_4, // 期望值 kinematics.fb_wheel_rpm.motor_4, // 反馈值 &pid[BR],// PID参数 0,// 单次积分限幅 0); // 积分限幅 pid[BR].out = Get_MiMx(pid[BR].out, -1.0, 1.0); // 输出限幅 // 将PID计算结果转换为PWM占空比 kinematics.pwm.motor_1 = -pid[FL].out; kinematics.pwm.motor_2 = -pid[FR].out; kinematics.pwm.motor_3 = -pid[BL].out; kinematics.pwm.motor_4 = -pid[BR].out; // 输出到电机 Set_PWM(); }

通过PID控制算法，我们可以精确的控制小车在各个方向的速度，从而实现对小车的精确控制。

Reference：

【麦克纳姆轮（万向轮）驱动原理及安装方法】

麦克纳姆轮（麦轮）原理

【学渣的自我修养】麦克纳姆轮浅谈

免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/130816.html