【博弈论5——合作博弈】

大家好，欢迎来到IT知识分享网。

1.帕累托最优

帕累托最优（Pareto Optimality）是经济学和决策理论中非常重要的一个概念，它描述了一种资源配置的状态，在这种状态下，任何改变都不可能使一部分人的境况变好而不使另一部分人的境况变差，即不存在所谓的帕累托改进（Pareto Improvement）。换句话说，如果一个经济体或者社会达到了帕累托最优，那么已经没有进一步调整资源配置的方式可以使得至少一个人受益而没有任何其他人受损。

2.合作博弈与数学表示

2.1 n人博弈的函数式

我们把$[I,V]$称为一个n人合作博弈，称$V(S)$为这个n人合作博弈的特征函数，其中S是I的任意子集（联盟），$V(S)$描述了联盟的效益。
特征函数式对n人合作博弈的每一种可能联盟都给出了对应的联盟收益，也就是给出了一种集合函数。

2.2 n人博弈中合作的方式

第一个情况：参与博弈的n个人形成一个合作联盟，称此联盟对应的博弈为n人大联盟合作博弈。n人大联盟合作博弈的解是指对大结盟所获利益$V(I)$的一个分配方案。
若用${\phi }_i(V(I)),i\in I$表示参与人i从n人大联盟合作博弈中获得的收益，则${\phi }_i(V(I))$至少应满足：
（1）个体合理性：KaTeX parse error: Undefined control sequence: \geV at position 16: \varphi_i(V(I))\̲g̲e̲V̲({i}),i\in I，即合作至少不比单干差。
（2）总体合理性：${\sum }_{i\in I}(V(I))=V(I)$,即将合作博弈$[I,V]$中获得的收益$V(I)$分光。
因此解决n人合作博弈问题的任务是如何获得一个合理的分配方案:
$$\varphi (V(I))=({\phi }_1(V(I)),{\phi }_2(V(I)),\dots ,{\phi }_n(V(I)))$$

第二种情形是：在参与人多余两个的情况下，就可能出现部分参与者联合起来追求小团体利益的行为，但其前提条件是参与者在小团体中得到的利益大或等于在大联盟中得到的利益，即存在子集$S=i_1,i_2,\dots ,i_k\subset I$，相应的总收益为$V(S)$，分配方案：
$$\varphi (V(S))=({\phi }_1(V(S)),{\phi }_2(V(S)),\dots ,{\phi }_n(V(S)))$$
满足,且其中至少有一个严格不等式成立。
$$\begin{gathered} {\phi }_{i_1}(V(S))\ge {\phi }_{i_1}(V(I)) \\ {\phi }_{i_2}(V(S))\ge {\phi }_{i_2}(V(I)) \\ \dots \dots \\ {\phi }_{i_k}(V(S))\ge {\phi }_{i_k}(V(I)) \end{gathered}$$

3.大联盟合作博弈中的效益分配——Shapley值计算

详见我的另外一篇博客：Shapley值的计算

4.大联盟合作博弈中如何量化决策影响力——班扎夫权利指数

班扎夫权利指数（Banzhaf Power Index, Banzhaf Power Measure），是由约翰·F·班扎夫三世（John F. Banzhaf III）在20世纪60年代提出的，它是量化投票系统中个体或团体决策影响力的指标，广泛应用于社会选择理论和政治科学中，尤其是在分析不同投票成员在集体决策中的相对权力。

在一个投票体系统中，比如使用多数规则（简单多数或特定比例多数）来决定议案是否通过的情况下，班扎夫权力指数衡量的是一个投票者可以通过改变自己的投票从导致议案不通过转变为通过的情况次数，或者是反过来，原本议案会通过但因其反对而无法通过的情况次数。

具体计算方法通常是通过穷举所有可能的投票组合，并统计每个投票者作为“关键票”的情况数量。关键票指的是如果该投票者改变其投票立场，则会导致投票结果发生改变的那张票。

5.其他联盟结构的求解方案

如何寻找联盟的稳定结构——核

解释：
在存在旁支付的情况下，2号联盟是合作博弈的核。
在不存在旁支付的情况下，1,2都是合作博弈的核。

核的定义

使得所有参与博弈的人员中的任何成员都不能从联盟重组中获益的结构，称为该合作博弈的核。

• 如果博弈的有效解集非空且有核，核一定包含在有效解集中。
• 有效解集中的许多解不是核。
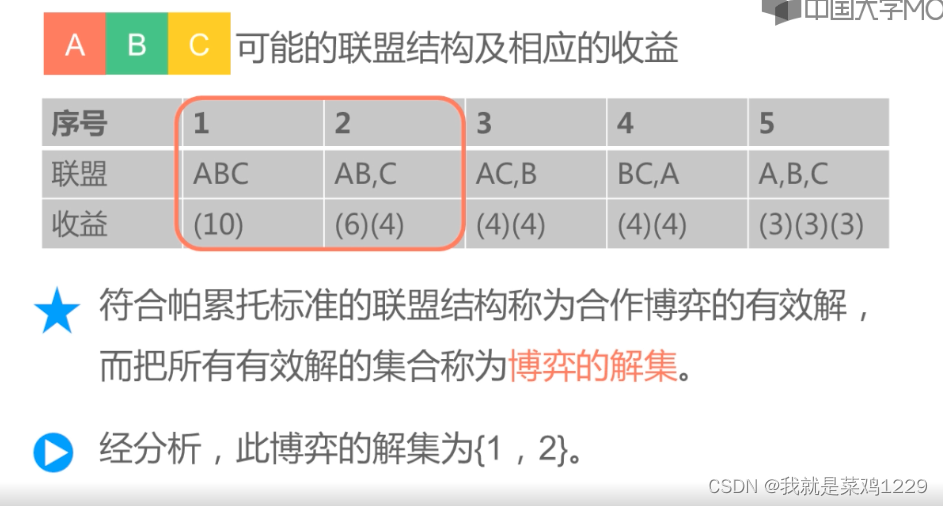
  • 符合帕累托标准的联盟结构称为合作博弈的的有效解
  • 所有有效解的集合称为博弈的解集
• 合作博弈的核可以有多个
• 核概念的致命缺点：经常为空

弱占优和强占优

合作博弈论解的其他概念

• 稳定集（Stable Set）
• 谈判集（Bargaining Set）
• 内核（Kernel）
• 核仁（Nucleolus）
• 纳什讨价还价解（Nash Bargaining Solution）