大家好，欢迎来到IT知识分享网。
1. 引言
Johann Heinrich Lambert（译为兰勃特，或兰伯特），瑞士裔德国科学家、哲学家，他首次给出了π为无理数的严格证明。1772年提出两种球面向投影面投影方式：等角圆锥投影和等积方位投影。通常所说的兰勃特投影指的是等角圆锥投影。
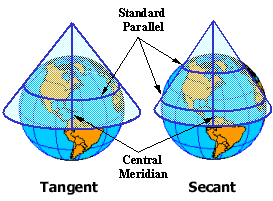
兰勃特等角圆锥投影是设想用一个正圆锥切于或割于球面，应用等角条件将地球面投影到圆锥面上，然后沿一母线展开成平面。投影后纬线为同心圆圆弧，经线为同心圆半径。兰勃特等角圆锥投影没有角度变形，经线长度比和纬线长度比相等。适于制作沿纬线分布的中纬度地区中、小比例尺地图。我国的分省图的兰伯特等角圆锥投影采用的两条标准纬度线为
=25度，=45度。
在北半球（左）和南半球（右）上以标准纬线显示了兰勃特等角圆锥投影。
2. 投影变换中所用符号
南方基准纬线：
北方基准纬线：
原点处纬度：
原点处经度：
变换点纬度：
变换点经度：
原点在投影坐标系中虚北向坐标：
原点在投影坐标系中虚东向坐标：
变换点假北向坐标：
变换点假东向坐标：
椭圆的长半轴：米（WGS-84椭球体）
椭圆的短半轴：米（WGS-84椭球体）
椭圆的扁率：
椭圆的第一偏心率：
其它中间参数：
3. 正变换（
）
4. 逆变换（
）
中间参数
其符号与相同
由此可获得相应的变换公式：
免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/135336.html
