复数的概念

大家好，欢迎来到IT知识分享网。

1. 虚数单位：i

引入一个新数 ‘i’，i又叫做虚数单位，并规定：

• 它的平方等于 -1，即 i² = -1。
• 实数可以与它进行四则运算，并且原有的加，乘运算律依然成立。

2.定义

• 复数的定义：形如 a + bi （a，b∈ R）的数叫做复数，其中a叫做复数的实部，b叫做复数的虚部。
• 复数的表示方法：复数通常用小写字母 z 表示，即 z = a + bi（a，b∈R），这种形式也称作复数的代数形式。
• 复数集:  全体复数构成的集合 C = {a + bi | （a，b ∈ R) }。

3. 分类 （重点）

数集之间的关系： N ⊆ Z ⊆ Q ⊆ R ⊆ C

4. 对比关系

• 实数之间可以比较大小，复数之间不可以比较大小，但可以相等。即实部 = 实部，虚部 = 虚部。
• Z1 = a + bi； Z2 = c + di；  若 Z1 = Z2，则 a = b且 c = d。

5. 共轭复数

实部相等，虚部相反的两个复数叫做共轭复数，复数Z的共轭复数用Z（上加一线）来表示。即

z = a + bi 与 z(上加一线) = a – bi 互为共轭复数。

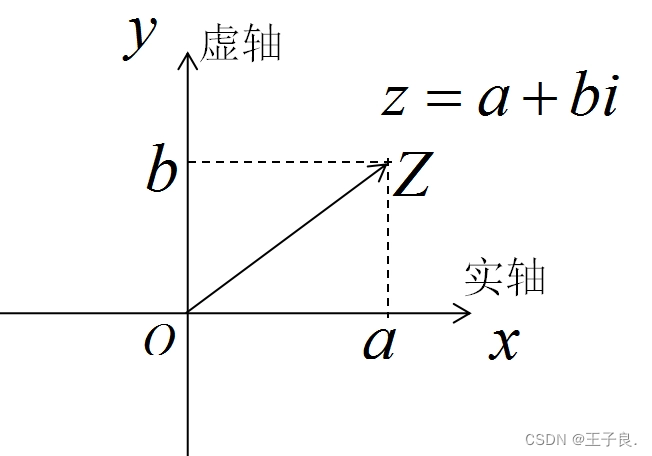
6. 复数的几何形式

{x轴：实轴， y轴：虚轴}

 7. 复数z的模

z = a + bi在复平面上对应的点 z(a,b）到远点的距离。

z = a + bi （a，b∈R）， |z| = 根号下 a² + b²