窄带干扰与宽带干扰的模型

大家好，欢迎来到IT知识分享网。

一、干扰分类

根据干扰信号的带宽可以把干扰分为窄带干扰（NBI）和宽带干扰（WBI）。

• 窄带干扰指的是带宽与发射信号带宽的比值较小或者其绝对带宽较小的干扰。
• 宽带干扰指的是带宽与发射信号带宽的比值较大或者其绝对带宽较大的干扰。
• 一般情况下，将干扰带宽小于整个SAR信号带宽的1%的干扰称作窄带干扰；干扰带宽与信号带宽的比大于10%时干扰被称作宽带干扰。

二、NBI

1. 定义式

对于窄带干扰，其频谱通常集中在较窄的频率范围内，在频域表现出一定的尖峰。通常情况下，可以将其看作一系列单频信号的叠加，因此可以将其表示为：
$$I_{NB}(n)=\sum _{l=1}^L{A}_l{e}^{j(2\pi f_{l}n+{\phi }_l)}$$
其中，$L$表示假设的单频干扰分量的个数，$A_l、f_l、{\phi }_l$分别为窄带干扰的第$l$个单频分量的幅度、频率和初始相位。

• 对于单个干扰分量而言，$A_l$是恒定的；$f_l、{\phi }_l$为常数。
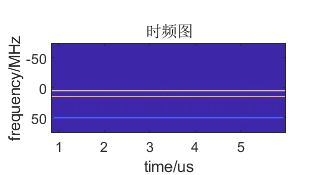
• 对单个干扰分量而言，其频率$f=\frac{1}{2\pi }\frac{d\theta (n)}{dn}=f_l$，因此其频谱在$f_l$处表现为一定的尖峰，而且在时频图上为平行与时间轴的直线。

2. 频谱图

3. 时频图

三、WBI

对于宽带干扰，它占有一定的带宽，在频域表现为一定带宽的凸起。

1. 线性调频宽带干扰

1.1 定义式

$$I_{CM}(n)=\sum _{l=1}^L{A}_l{e}^{j(2\pi f_{l}n+\pi g_l{n}^2)}$$
其中，$L$为调频干扰个数，$A_l,f_l,g_l$分别为宽带干扰的第$l$个载波频率分量的幅度，频率和调频率。

• 对于单个干扰分量而言，$A_l$是恒定的；$f_l、g_l$为常数。
• 对单个干扰分量而言，其频率$f=\frac{1}{2\pi }\frac{d\theta (n)}{dn}=f_l+g_{l}n$，因此其频谱表现为一定宽度的凸起，而且在时频图上表现为斜率为$g_l$的直线。

1.2 频谱图

1.3 时频图

2. 正弦调频宽度干扰

2.1 定义式

$$I_{SM}(n)=\sum _{l=1}^L{A}_l{e}^{j{\beta }_{l}sin(2\pi f_{l}n+{\varphi }_l)}$$
其中，$A_l,{\beta }_l,f_l与{\varphi }_l$分别表示第$l(l=1,\cdots ,L)$个干扰分量的幅度、调制系数、频率和初始相位。

• 对于单个干扰分量而言，$A_l$是恒定的；${\beta }_l、f_l、{\varphi }_l$为常数。
• 正弦调频宽带干扰的频率取值是十分关键的，仿真过程中若$f_l$取值不合适，很有可能得不到我们期望的结果。此外，调制系数也对仿真结果有着很大的影响。
• 对单个干扰分量而言，其频率$f=\frac{1}{2\pi }\frac{d\theta (n)}{dn}=f_l{\beta }_{l}cos(2\pi f_{l}n+{\varphi }_l)$，因此其频谱表现为一定宽度的凸起，而且在时频图上表现为余弦形式。

2.2 频谱图

2.3 时频图