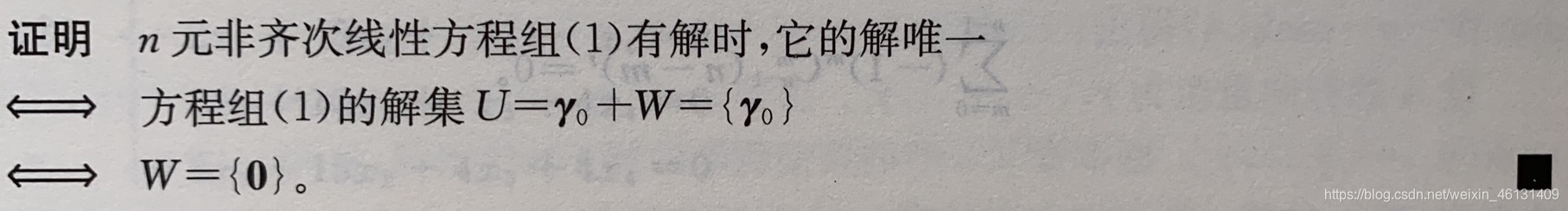大家好,欢迎来到IT知识分享网。
零.引入
利用行列式可以判定数域K上n个方程的n元线性方程组是否有唯一解,并可给出唯一解的公式表示,但不能分别无解和有无穷多个解的情况;因此需要新的方法来通过系数和常数项判定线性方程组是否有解,有多少个解,以及有无穷多个解时解集的结构
一.n维向量空间 K n K^n Kn及其子空间(3.1)
1.向量空间中的加法/数量乘法/运算法则:
8条运算法则中的前4条是关于加法的,后4条是关于数量乘法的 2.n维向量空间的定义:
3.线性表出:
4.线性子空间
(1)概念:
(2)命题1:
二.线性相关与线性无关(3.2)
1.定义:
2.线性相关与线性无关的向量组的比较
(1)从线性组合看:
向量组 α 1 , α 2 . . . α s ( s ≥ 1 ) α_1,α_2…α_s(s≥1) α1,α2...αs(s≥1)线性相关⇔ ∃ k 1 2 + . . . + k s 2 ≠ 0 ∃k_1^2+…+k_s^2≠0 ∃k12+...+ks2=0使 k 1 α 1 + . . . + k s α s = 0 k_1α_1+…+k_sα_s=0 k1α1+...+ksαs=0
向量组 α 1 , α 2 . . . α s ( s ≥ 1 ) α_1,α_2…α_s(s≥1) α1,α2...αs(s≥1)线性无关⇔当且仅当 k 1 2 + . . . + k s 2 = 0 k_1^2+…+k_s^2=0 k12+...+ks2=0, k 1 α 1 + . . . + k s α s = 0 k_1α_1+…+k_sα_s=0 k1α1+...+ksαs=0
(2)从线性表出看:
向量组 α 1 , α 2 . . . α s ( s ≥ 2 ) α_1,α_2…α_s(s≥2) α1,α2...αs(s≥2)线性相关⇔其中至少有1个向量可由其余向量线性表出
向量组 α 1 , α 2 . . . α s ( s ≥ 2 ) α_1,α_2…α_s(s≥2) α1,α2...αs(s≥2)线性无关⇔其中任何1个向量都不能由其余向量线性表出
(3)从齐次线性方程组看:
列向量组 α 1 , α 2 . . . α s ( s ≥ 1 ) α_1,α_2…α_s(s≥1) α1,α2...αs(s≥1)线性相关⇔齐次线性方程组 x 1 α + . . . + x s α s = 0 x_1α_+…+x_sα_s=0 x1α+...+xsαs=0有非0解
列向量组 α 1 , α 2 . . . α s ( s ≥ 1 ) α_1,α_2…α_s(s≥1) α1,α2...αs(s≥1)线性无关⇔齐次线性方程组 x 1 α + . . . + x s α s = 0 x_1α_+…+x_sα_s=0 x1α+...+xsαs=0只有0解
(4)从行列式看:
n个n维列(或行)向量 α 1 , α 2 . . . α n α_1,α_2…α_n α1,α2...αn线性相关⇔以 α 1 , α 2 . . . α n α_1,α_2…α_n α1,α2...αn为列(或行)向量组的矩阵的行列式等于0
⇔n个n维列(或行)向量 α 1 , α 2 . . . α n α_1,α_2…α_n α1,α2...αn线性无关⇔以 α 1 , α 2 . . . α n α_1,α_2…α_n α1,α2...αn为列(或行)向量组的矩阵的行列式不等于0
(5)从线性表出看:
设向量 β \beta β可由向量组 α 1 , α 2 . . . α n α_1,α_2…α_n α1,α2...αn线性表出
则向量组 α 1 , α 2 . . . α n α_1,α_2…α_n α1,α2...αn线性相关⇔表出方式有无穷多种
向量组 α 1 , α 2 . . . α n α_1,α_2…α_n α1,α2...αn线性无关⇔表出方式唯一
(6)从向量组与其部分组的关系看:
(7)从向量组与其延伸(或缩短)组的关系看:
如果向量组线性无关,则给每个向量加上m个分量(加上的分量的位置对每个向量都相同)而得到的延伸组也线性无关
如果向量组线性相关,则把每个向量去掉m个分量(去掉的分量的位置对每个向量都相同)而得到的缩短组也线性相关(这是前半部分的逆否命题)
3.线性相关与线性表出:
定理1:设向量组 α 1 , α 2 . . . α s α_1,α_2…α_s α1,α2...αs线性无关,则向量 β \beta β可由 α 1 , α 2 . . . α s α_1,α_2…α_s α1,α2...αs线性表出的充要条件是: α 1 , α 2 . . . α s , β α_1,α_2…α_s,\beta α1,α2...αs,β线性相关
推论:设向量组 α 1 , α 2 . . . α s α_1,α_2…α_s α1,α2...αs线性无关,则向量 β \beta β不能由 α 1 , α 2 . . . α s α_1,α_2…α_s α1,α2...αs线性表出的充要条件是: α 1 , α 2 . . . α s , β α_1,α_2…α_s,\beta α1,α2...αs,β线性无关
定理2:如果向量 β \beta β可由向量组 α 1 , α 2 . . . α s α_1,α_2…α_s α1,α2...αs线性表出,则表达方式唯一的充要条件是: α 1 , α 2 . . . α s α_1,α_2…α_s α1,α2...αs线性无关
4.一些性质:
定理3:在 K n K^n Kn中,∀ n + 1 n+1 n+1个向量都线性相关
定理4(替换定理):设 α 1 , α 2 . . . α s α_1,α_2…α_s α1,α2...αs线性无关, β = b 1 α 1 + . . . + b s α s \beta=b_1α_1+…+b_sα_s β=b1α1+...+bsαs,如果 b i ≠ 0 b_i≠0 bi=0,则用 β \beta β替换 α i \alpha_i αi后,向量组 α 1 . . . α i − 1 , β , α i + 1 . . . α s α_1…α_{i-1},\beta,α_{i+1}…α_s α1...αi−1,β,αi+1...αs仍线性无关;如果 b i = 0 b_i=0 bi=0,则用 β \beta β替换 α i \alpha_i αi后,向量组 α 1 . . . α i − 1 , β , α i + 1 . . . α s α_1…α_{i-1},\beta,α_{i+1}…α_s α1...αi−1,β,αi+1...αs线性相关
三.最大线性无关组与向量组的秩(3.3)
- 最大线性无关组又称极大线性无关组
1.定义:
2.向量组的等价
(1)定义:
(2)性质:
①反身性:任何1个向量组都与自身等价
②对称性:如果 { α 1 . . . α s } ≅ { β 1 . . . β s } \{α_1…α_s\}\cong\{β_1…β_s\} {
α1...αs}≅{
β1...βs},则 { β 1 . . . β s } ≅ { α 1 . . . α s } \{β_1…β_s\}\cong\{α_1…α_s\} {
β1...βs}≅{
α1...αs}
③传递性:如果 { α 1 . . . α s } ≅ { β 1 . . . β s } , { β 1 . . . β s } ≅ { γ 1 . . . γ s } \{α_1…α_s\}\cong\{β_1…β_s\},\{β_1…β_s\}\cong\{γ_1…γ_s\} {
α1...αs}≅{
β1...βs},{
β1...βs}≅{
γ1...γs},则 { α 1 . . . α s } ≅ { γ 1 . . . γ s } \{α_1…α_s\}\cong\{γ_1…γ_s\} {
α1...αs}≅{
γ1...γs}
3.命题2:
向量组与其最大线性无关组等价
推论1:向量组的∀2个最大线性无关组等价
推论2: β \beta β可由向量组 α 1 . . . α s α_1…α_s α1...αs线性表出的充要条件是: β \beta β可由 α 1 . . . α s α_1…α_s α1...αs的1个最大线性无关组线性表出
设向量组 β 1 . . . β r β_1…β_r β1...βr可由向量组 α 1 . . . α s α_1…α_s α1...αs线性表出,如果 r > s r>s r>s,则 β 1 . . . β r β_1…β_r β1...βr线性相关
推论1:设向量组 β 1 . . . β r β_1…β_r β1...βr可由向量组 α 1 . . . α s α_1…α_s α1...αs线性表出,如果 β 1 . . . β r β_1…β_r β1...βr线性无关,则 r ≤ s r≤s r≤s
推论2:等价的线性无关的向量组所含向量的个数相同
推论3:向量组的∀2个最大线性无关组所含向量的个数相同
(2)向量组的秩的定义:
(3)秩与线性无关:
命题3:向量组 α 1 . . . α s α_1…α_s α1...αs线性无关的充要条件是: r a n k { α 1 . . . α s } < s rank\{α_1…α_s\}<s rank{
α1...αs}<s
(4)秩与线性表出:
命题4:如果向量组 ( Ⅰ ) (Ⅰ) (Ⅰ)可由向量组 ( Ⅱ ) (Ⅱ) (Ⅱ)线性表出,则: r a n k { ( Ⅰ ) } ≤ r a n k { ( Ⅱ ) } rank\{(Ⅰ)\}≤rank\{(Ⅱ)\} rank{
(Ⅰ)}≤rank{
(Ⅱ)}
命题5:等价的向量组有相等的秩
注意:逆命题不成立,如:
四.基与维数(3.4)
1.基
(1)定义:
显然, ε 1 = ( 1 , 0…0 ) ′ , ε 2 = ( 0 , 1…0 ) ′ . . . ε n ( 0 , 0…1 ) ′ ε_1=(1,0…0)’,ε_2=(0,1…0)’…ε_n(0,0…1)’ ε1=(1,0...0)′,ε2=(0,1...0)′...εn(0,0...1)′是 K n K^n Kn的1个基,称其为 K n K^n Kn的标准基
(2)定理5:
K n K^n Kn的任一非零子空间U都有1个基
(3)定理6:
K n K^n Kn的非零子空间U的∀2个基所含向量的个数相等
可通过”等价的线性无关的向量组含有相同个数的向量”这一结论证明该定理
2.维数
3.坐标:
4.基与维数对子空间结构的影响
命题6:设dim U=r,则U中∀r+1个向量都线性相关
命题7:设dim U=r,则U中∀r个线性无关的向量都是U的1个基
命题8:设dim U=r,α1,α2…αr∈U,如果U中每个向量都可由α1…αr线性表出,则α1…αr是U的1个基
命题9:设U和W都是Kn的非零子空间,如果 U ⊆ W U\subseteq W U⊆W,则dim U≤dim W
命题10:设U和W是Kn的2个非零子空间,且 U ⊆ W U\subseteq W U⊆W,如果dim U=dim W,则U=W
定理7:向量组α1…αs的1个最大线性无关组是这个向量组生成的子空间<α1…αs>的1个基,从而dim<α1…αs>=rank{α1…αs}
5.行空间与列空间:
五.矩阵的秩(3.5)
1.列秩与行秩
(1)概念:
(2)列秩与行秩的关系:
定理8:阶梯型矩阵J的行秩与列秩相等,且均等于J的非零行的个数,且J的主元所在的列构成列向量组的1个最大线性无关组
定理12:任一矩阵A的行秩等于其列秩
(3)初等变换与行(或列)秩:
定理10:矩阵的初等行变换不改变矩阵的行秩
定理11:矩阵的初等行变换不改变矩阵的列向量组的线性相关性,因而不改变矩阵的列秩,即:
2.矩阵的秩
(1)定义:
(2)性质:
推论1:设矩阵A经过初等行变换转化成阶梯型矩阵J,则rank(A)等于J的非零行个数;设J的主元所在的列是第 j 1 . . . j r j_1…j_r j1...jr列,则A的第 j 1 . . . j r j_1…j_r j1...jr列构成A的列向量组的1个最大线性无关组
推论2:矩阵的初等列变换不改变矩阵的秩
定理12:任一非零矩阵的秩都等于其不为零的子式的最高阶数
该定理给出了求矩阵的秩的另1种方式
定理11和定理12表明:
推论3:设s×n矩阵A的秩为r,则A的不等于零的r阶子式所在的行(或列)构成A的行(或列)向量组的1个最大线性无关组
3.满秩矩阵
(1)定义:
(2)判定:
推论4:n阶矩阵A满秩的充要条件是:|A|≠0
六.线性方程组的解(3.6,3.7,3.8)
1.线性方程组的解的情况的判定
(1)线性方程组有解判别定理:
定理13:数域K上线性方程组 x 1 α 1 + x 2 α 2 + . . . + x n α n = β ( 1 ) x_1α_1+x_2α_2+…+x_nα_n=β\uad(1) x1α1+x2α2+...+xnαn=β(1)有解的充要条件是:其系数矩阵和增广矩阵的秩相等
(2)判别线性方程组的解的个数:
定理14:数域K上n元线性方程组(1)有解时,如果其系数矩阵A的秩等于n,则其有唯一解;如果A的秩小于n,则其有无穷多个解
推论1:数域K上n元齐次线性方程组有非零解的充要条件是:其系数矩阵的秩小于未知量的个数n
概念:
齐次线性方程组的解向量的性质:
①若 γ , δ ∈ W γ,δ∈W γ,δ∈W,则 γ + δ ∈ W γ+δ∈W γ+δ∈W
②若 γ ∈ W , k 属 于 K γ∈W,k属于K γ∈W,k属于K,则 k γ ∈ W kγ∈W kγ∈W
(2)解空间:
定理15:数域K上n元齐次线性方程组的解空间W的维数 d i m W = n − r a n k ( A ) dim W=n-rank(A) dimW=n−rank(A)其中A是方程组的系数矩阵;从而当(1)有非零解时,其每个基础解系所含向量的个数都等于 n − r a n k ( A ) n-rank(A) n−rank(A)
(3)基础解系:
3.非齐次线性方程组的解集的结构
(1)导出组:
(2)非齐次线性方程组的解向量的性质:
性质1:若 γ , δ ∈ U γ,δ∈U γ,δ∈U,则 γ − δ ∈ W γ-δ∈W γ−δ∈W
性质2:若 γ ∈ U , η ∈ W γ∈U,η∈W γ∈U,η∈W,则 γ + η ∈ U γ+η∈U γ+η∈U
(3)非齐次线性方程组的解集:
定理16:如果数域K上(1)有解,则其解集 U = { γ 0 + η ∣ η ∈ W } U=\{γ_0+η | η∈W\} U={
γ0+η∣η∈W}其中 γ 0 γ_0 γ0是(1)的1个解,称为特解;W是其导出组(2)的解空间
将集合U记作 γ 0 + W γ_0+W γ0+W,称其是1个W型的线性流形(或子空间W的1个配集),把 d i m W dim W dimW称为线性流形 γ 0 + W γ_0+W γ0+W的维数
注意:n元齐次线性方程组的解集W是 K n K^n Kn的1个子空间,但n元非齐次线性方程组的解集U不是子空间(因为对加法/数乘都不封闭);U是1个W型的线性流形,其中W是其导出组的解空间
求解非齐次线性方程组(1):
(4)非齐次线性方程组的解的个数的判定:
推论1:如果(1)有解,则其解唯一的充要条件是:其导出组(2)只有零解
附:代数运算
1.非空集合S上的1个代数运算是指S×S(S与自身的笛卡尔积)到S的1个映射
2.代数编码理论
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/146364.html