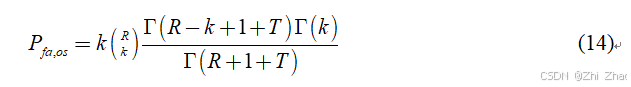【目标检测】雷达目标CFAR检测算法

大家好，欢迎来到IT知识分享网。

一、概述

1、基本概念

2、基础知识

雷达在判决过程中，可能会出现两类错误。第一类是在没有目标时判断为有目标，这类错误称为虚警。另一类是在有目标时判断为没有目标，这类错误称为漏警。以上两类错误以一定的概率出现，分别称为虚警概率和漏警概率。

二、CFAR检测算法

目前，研究人员针对各种杂波环境下提出了许多高效的CFAR检测算法，大体可分为两类：一类是均值类CFAＲ(CA-CFAＲ)算法，该类算法应用的前提是假设背景杂波是均匀分布的；另一类是有序统计类CFAＲ(OS-CFAＲ)算法，这类算法是为了应对邻域内多目标情况而设计的。不同CFAR检测算法各有优劣，都是针对具体情况而设计，我们只需要学习CFAR的基本原理以及熟悉几种典型的CFAR检测算法即可。

1、基本原理

CFAR检测器的输入一般包括检测单元 $Y$ 和 $2n$ 个参考单元。参考单元位于检测单元两侧，前后各 $n$ 个。保护单元主要用在单目标情况下，防止目标能量泄漏到参考单元影响检测效果。设参考门限电平为 $V_{TH}$，$V_{TH}=T\times Z$，其中：$Z$ 为总的杂波功率水平的估计，$T$ 为门限因子，则当$Y>V_{TH}$ 时，认为有目标；反之，认为没有目标。
CFAR算法的处理流程如下图所示：

一般情况下，杂波同噪声相互独立，且平方律检波后都满足指数分布。参考单元的概率密度函数为：

设 $H_0$ 表示为没有目标，$P[Y>TZ|H_0]$ 则表示为在没有目标的条件下判断为有目标的概率，从而得到虚警概率的表达式为：

式中，$\mu$ 是噪声功率；$Z$ 为随机变量，它的分布取决于CFAR算法的类型以及参考单元的分布；$M_Z(u{)}_{u=T/2\mu }$ 为矩母函数。

2、几种典型的CFAR检测算法

不同类型CFAR算法的差异主要体现为对参考单元处理的不同，亦为 $Z$ 值选取的不同。在背景噪声独立同分布时，通过确定常数 $T$ 来达到恒定的虚警概率。不同的检测算法，其确定常数 $T$ 的方法也会相应的有所区别。下面将对几种典型CFAR算法的虚警概率表达式进行推导。

（1）CA(Cell Averaging)-CFAR检测算法

背景杂波功率水平 $Z$ 的计算方式为 $2n$个参考单元之和：
$$Z=\sum _{i=1}^n{X}_i+\sum _{i=n+1}^{2n}{X}_i=\sum _{i=1}^{2n}{X}_i$$
在推导 $P_{fa}$ 与 $T$ 的关系之前，我们先给出伽马(Γ)分布的相关知识。
$\Gamma$ 分布的概率密度函数为：

其中，$\alpha ，\beta$ 是两个参数，当 $\alpha =1，\beta =2\mu$时，式(3)就退化成为式(1)中的指数分布；$\Gamma (\alpha )$就是数学中的伽马函数，对于正整数 $\alpha$，有 $\Gamma (\alpha )=(\alpha -1)！$。
设 $G(\alpha ,\beta )$ 为 $\Gamma$ 分布的概率分布函数，若 $X$ 为服从 $\Gamma$ 分布的随机变量，则有 ：

$X$ 的矩母函数为：

假设输入信号中的各变量满足独立同分布的条件，则对于 $2n$个随机变量之和的矩母函数等于各随机变量的矩母函数之积，所以有：

将式(5)和式(6)以及 $u=T/2\mu$ 代入式(2)，可得：

即可得到虚警概率 $P_{fa}$ 与门限因子 $T$ 的关系：

（2）GO-CFAR、SO-CFAR检测算法

最大选择GO(Greatest Of)-CFAR是选取前面 $n$ 个参考单元之和与后面 $n$ 个参考单元之和中的大者作为背景杂波功率水平 $Z$ ；而最小选择SO(Smallest Of)-CFAR是选取前面 $n$ 个参考单元之和与后面 $n$ 个参考单元之和中的小者作为背景杂波功率水平 $Z$。

对于GO-CFAR算法，Z的概率密度函数为 $f_Z(z)$，进而推导其虚警概率为 $P_{fa,go}$，如下式：

同理，可得到SO-CFAR算法的概率密度函数为 $f_Z(z)$，虚警概率为$P_{fa,so}$，如下式：

（3）OS-CFAR检测算法

顺序统计量OS(Order Statistic)CFAR的原理是先对参考单元从小到大排序，再选取第 $k$ 个样本作为$Z$。
设 OS-CFAR 算法的虚警概率为 $P_{fa,os}$，根据参考文献中的公式推导可得：

$R=2n$，$k$ 为OS-CFAR中的参数，其值的选取对算法的检测性能有较大影响。

(4) 补充说明

GO、SO、OS三类CFAR检测算法的门限因子 $T$ 难以用数学表达式表示，可以通过迭代运算的方式求解出来。
当求解出门限因子 $T$ 后，便可以将其代入检测概率的表达式，得到在不同信噪比的条件下，检测概率的变化情况。
在参考文献[4]和[5]中给出了检测概率 $P_d$ 的计算方法。

三、不同CFAR检测算法性能对比

1、MATLAB仿真结果

为了比较不同CFAR算法的检测性能，建立CA、GO、SO、OS四类CFAR算法的检测概率与信噪比的关系曲线，信噪比设置为0~30dB，参考单元的数目 $2n$ 分别取16、24、32、48、64、128，保护单元左右各3个，虚警概率 $P_{fa}=10^{-6}$。
MATLAB仿真结果如下图所示。

2、MATLAB代码

% ------ 程序功能：四类CFAR检测算法的检测概率与SNR的关系 % clc clear all; close all; %% 参数设置 R = 24; % 参考单元长度 n = R/2; % 半滑窗长度 k = R*3/4; % os-cfar的参数 P_fa = 1e-6; % 虚警概率 SNR_dB = (0:30); % 信噪比 SNR = 10.^(SNR_dB./10); % 信号功率与噪声功率的比值 syms T; % 门限因子的符号变量 %% CA-CFAR T_CA = P_fa^(-1/R)-1; % CA-CFAR的门限因子 Pd_CA = (1+T_CA./(1+SNR)).^(-R); % CA-CFAR的检测概率 %% SO-CFAR、GO-CFAR Pfa_SO = 0; syms T for i = 0:n-1 Pfa_SO = Pfa_SO+2*nchoosek(n+i-1,i)*(2+T)^(-(n+i)); % SO-CFAR的虚警概率表达式 end T1_SO = solve(Pfa_SO == P_fa, T); % 求解出虚警概率为P_fa时对应的门限因子T T2_SO = double(T1_SO); T_SO = T2_SO(T2_SO == abs(T2_SO)); % SO-CFAR的门限因子 Pfa_GO = 2*(1+T)^(-n)-Pfa_SO; % GO-CFAR的虚警概率表达式 T1_GO = solve(Pfa_GO == P_fa, T); % 求解出虚警概率为P_fa时对应的门限因子T T2_GO = double(T1_GO); T_GO = T2_GO(T2_GO == abs(T2_GO)); % GO-CFAR的门限因子 Pd_SO = 0; Pd_GO = 0; for j = 0:n-1 Pd_SO = Pd_SO+2*nchoosek(n+j-1,j).*(2+T_SO./(1+SNR)).^(-(n+j)); % SO-CFAR的检测概率 Pd_GO = Pd_GO+2*nchoosek(n+j-1,j).*(2+T_GO./(1+SNR)).^(-(n+j)); end Pd_GO = 2.*(1+T_GO./(1+SNR)).^(-n)-Pd_GO; % GO-CFAR的检测概率 %% OS-CFAR Pfa_OS = k*nchoosek(R,k)*gamma(R-k+1+T)*gamma(k)/gamma(R+T+1); % OS-CFAR的虚警概率表达式 T1_OS = solve(Pfa_OS == P_fa, T); % 求解出虚警概率为P_fa时对应的门限因子T T2_OS = double(T1_OS); T_OS = T2_OS(T2_OS == abs(T2_OS)); % OS-CFAR的门限因子 Pd_OS = k*nchoosek(R,k)*gamma(R-k+1+T_OS./(1+SNR))*gamma(k)./gamma(R+T_OS./(1+SNR)+1); % OS-CFAR的检测概率 %% 画图 figure; plot(SNR_dB,Pd_CA,'r-*'); hold on; plot(SNR_dB,Pd_SO,'k-^'); plot(SNR_dB,Pd_GO,'b-o'); plot(SNR_dB,Pd_OS,'m-.'); grid on; xlabel('SNR','FontName','Time New Romans','FontAngle','italic'); ylabel('P_{d}','FontName','Time New Romans','FontAngle','italic'); title(['恒虚警率 P_{fa}= ',num2str(P_fa),'，参考单元 2n= ',num2str(R)]); legend('CA','SO','GO','OS'); 

3、优缺点总结

在实际应用中，由于雷达的硬件运算资源有限，较普遍采用的算法依然复杂度较低的CA-CFAR检测算法。

四、参考文献