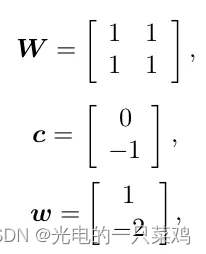两小时看完花书（深度学习入门篇）

大家好，欢迎来到IT知识分享网。

1.深度学习花书前言

1. 机器学习基础知识：涵盖线性代数，概率论，数值计算和传统机器学习基础等知识。如果之前学过Andrew Ng的CS229的话基本可以跳过。
2. 深度神经网络核心知识：属于本书必读部分，涵盖前馈神经网络，卷积神经网络（CNN)，递归神经网络（RNN) 等。
3. 深度学习前沿：有一些前沿研究领域的介绍，如线性因子模型，表征学习，生成模型等。

2.三要素

2.1任务

2.2性能指标

2.3经验

3.欠拟合与过拟合的本质

我们的机器学习模型因此有两个主要目的：

4.正则化方法

5.超参数与验证集

  初学者可能对参数与超参数(hyperparameter)的区别不是很清晰。用多次项拟合例子来说，参数就是指其中每项的权重$w$的值，合适的$w$是通过机器学习得到的，而超参数是我们选取用几次多项式来描述，也可以看做模型容量超参数，另外还有正则项系数$\lambda$取什么值，这些通常是人为设定的。有些超参数是无法用训练集习得的，例如模型容量超参数，如果仅对训练集来说总会选取更大的模型容量，使得训练误差减小，但会造成过拟合，同样的，对于正则项，仅对训练集学习会使得正则项为零而使训练误差更小，也造成过拟合。
  为了解决这个问题，我们需要一个区别于训练集的验证集(validation set)。我们可以将训练集分成两部分，一部分对于固定的超参数得到合适的参数w，而另一部分作为验证集来测试该模型的泛化误差，然后对超参数进行适宜的调整。简单概括就是训练集是为了选取合适的参数，而验证集是为了选取合适的超参数。

6. 前馈神经网络

  前馈神经网络（Deep feedforward network) 可以说是深度学习最核心的模型之一。前馈神经网络的目的是对于输入 $x$，假设我们要模拟从输入到输出的真实函数$f\ast$，神经网络想要找到这样的映射 $y=f(x;\theta )$和合适的参数$\theta$使得其预测尽量接近真实函数$f\ast$。
  其中，前馈代表了所有的信息都从输入经过某些中间的计算而最终输出到 ，而不存在从模型的输出到输入的反馈(feedback），对于有反馈的情况即为循环神经网络(recurrent neural network)。前馈网络已经广泛应用在工业界，其重要性不言而喻，而且它也是理解在自然语言处理中应用广泛的循环神经网络的基础。
  而网络则代表了该模型是将不同的基本函数组合在一起形成的模型。例如通过将三个函数$f^{(1)}$,$f^{(2)}$,$f^{(3)}$串联起来构成最终的函数$f(x)=f^{(3)}(f^{(2)}(f^{(1)}(x)))$，$f^{(1)}$就是网络的第一层，$f^{(2)}$就是网络的第二层，以此类推。这个链的长度又被称作网络的深度（depth)，深度学习也因此得名。而前馈网络的最后一层被称作输出层(output layer)，对于我们的训练数据，每一个输入 $x$都有相应的标记$y=f^{\ast }(x)$，而网络的输出层的结果需要尽量接近 y。但对于其它层来说，和训练数据没有这样的直接对应关系，即我们的算法只要求最后的输出接近于真实的标记，而对于中间每层的目的并没有明确定义，所以这些层又被称作隐藏层(hidden layer)。
  最后，神经代表了它的灵感部分受到了神经科学的影响。每一隐藏层通常是矢量值，而这些隐藏层的维度定义了网络的宽度。我们可以将每层看做从一个大的从矢量到矢量的函数映射，但从另一方面也可以将矢量的每个元素看做一个小的神经元，每个神经元进行了矢量到标量的映射操作（这一操作又被称作激活函数，activation function），而每一层是不同的神经元并行运算的综合。
  前馈神经网络的提出是为了解决传统线性模型的一些限制。线性模型如逻辑回归或者线性回归的优势是我们有的可以快速求出解析解，有的可以利用convex optimization来解决。但同时，线性模型也受限于只能模拟线性关系，而很难学习不同输入参数间的关系。为了将线性模型扩展到非线性函数，我们可以对于输入$x$做非线性变换，再利用对于的线性模型解决该问题。

6.1如何选取映射

  选取一个比较通用的$f^{\ast }$，例如kernel trick中的RBF kernel（也称作Gaussian kernel），如果的维度足够高，我们总能够使其匹配训练集，但很难推广到测试集。因为这种模型只是假设了局域变化不大的前提，而并没有包含任何有价值的先验信息。
  人工选取合适的 $f^{\ast }$，实际上这是在深度学习流行之前普遍采用的方法，但是这需要大量的相关经验与人力资源，而且不同领域间的知识很难迁移。
  深度学习的策略是利用神经网络学习合适的用隐藏层代表的映射 $f^{\ast }$,即模拟$y=f(x;\theta ;w)=f^{\ast }(x;\theta {)}^{T}w$,其中 $\theta$是 $f^{\ast }$的模拟参数,而 $w$是从$f^{\ast }$到最终输出的映射参数。它结合了第一和第二种方法，我们可以从比较通用的函数家族中学习 $f^{\ast }$，同时也可以利用经验对函数家族的选择进行一些限制。与第二种方法比较，其优势在于我们只需要找到一个比较合适的函数家族，而不需要知道确切的函数。

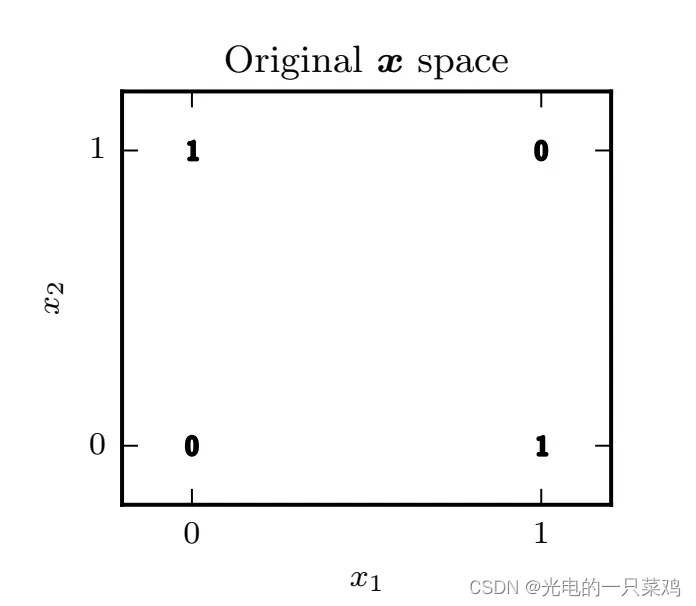
6.2用神经网络模拟XOR

  从图中可以看出，我们无法对该空间进行线性分割，使得两个输出为1的点落在分割线同一侧，而两个输出为0的点落在分割线另一侧。所以，传统的线性模型无法解决这一问题。为了解决这个问题，我们需要找到一个新的特征空间，使得在新空间中能用线性模型来解决。
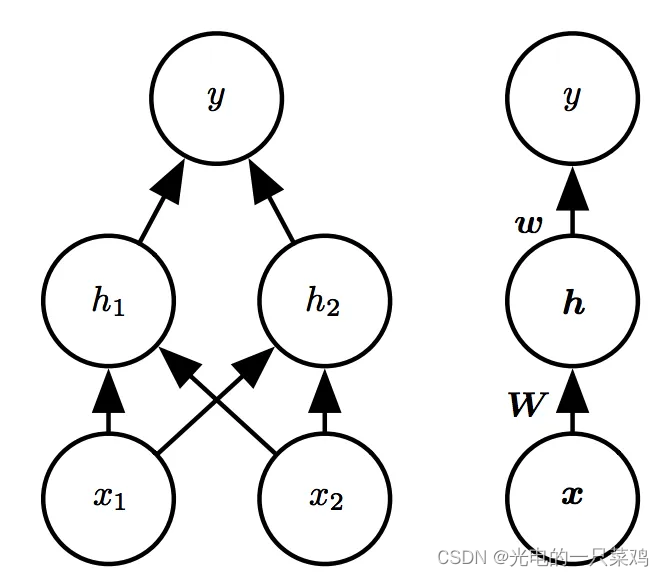
  我们引入一个如下图所示的简单的具有一层隐藏层的前馈网络模型：注意图中两种方式表示是等价的，左图是具体画出每个节点，而右图是简化为层。

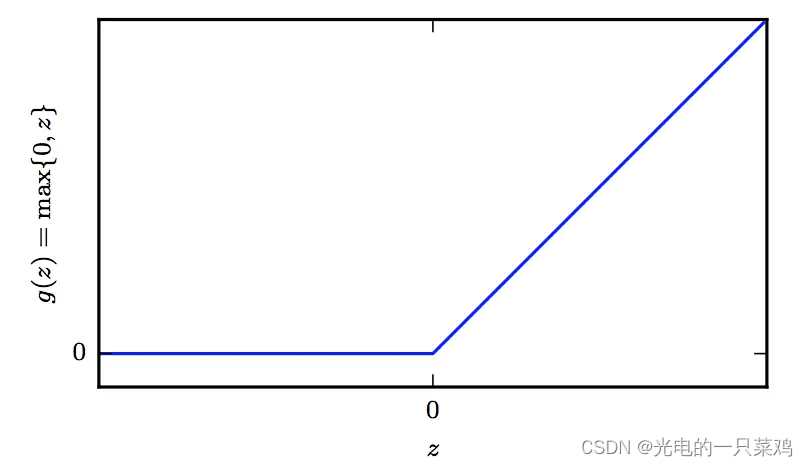
  假设我们用 $h=f^{(1)}(x;W;c)$模拟从输入到到隐藏层的映射，而用$y=f^{(2)}(h;w,b)$模拟从隐藏层到输出的线性映射，则整个模型可以表示为$f(x;W,c,w,b)=f^{(2)}(f^{(1)}(x))$, 那我们如何选取$f^{(1)}$呢，通常在神经网络中我们选称作rectified linear unit，简称为RELU的激活函数，其形式为$g(z)=max0,z$

  同时选取$h=f^{(2)}$ 为线性函数，我们的模型转化为$f(x;W,c,w,b)=w^{T}max(0,W^{T}x+c)+b$,我们的输入用矩阵表示为

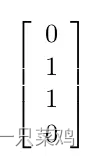
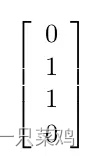
而希望模拟的对应的输出是
对于我们的模型，我们可以找到如下的解

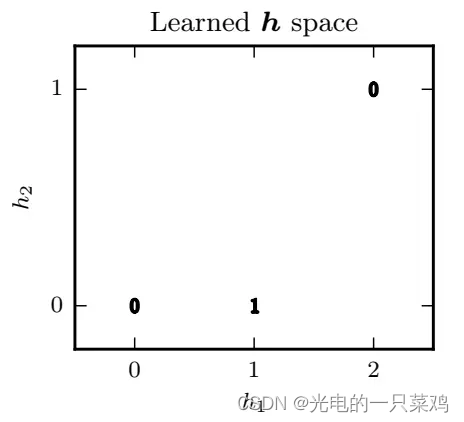
即我们已经从原空间映射到隐藏层所代表的空间

  可以看到在新空间中，原来的输出为1的两个点已经汇聚在同一点 h=[1,0]
，因此我们可以找到该空间的线性分割，使得两个输出为1的点落在分割线同一侧，而两个输出为0的点落在分割线另一侧。我们继续将h，w，b代入可得最终输出

7.损失函数

8.反向传播

9.提升模型泛化能力的方法

10.优化方法归纳

11.卷积神经网络

12.循环神经网络

13.对抗神经网络