大家好,欢迎来到IT知识分享网。
复杂度的概念
算法在编写成可执⾏程序后,运⾏时需要耗费时间资源和空间(内存)资源 。因此衡量⼀个算法的好 坏,⼀般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量⼀个算法的运⾏快慢,⽽空间复杂度主要衡量⼀个算法运⾏所需要的额外空间。 在计算机发展的早期,计算机的存储容量很⼩。所以对空间复杂度很是在乎。但是经过计算机⾏业的 迅速发展,计算机的存储容量已经达到了很⾼的程度。所以我们如今已经不需要再特别关注⼀个算法 的空间复杂度。
时间复杂度
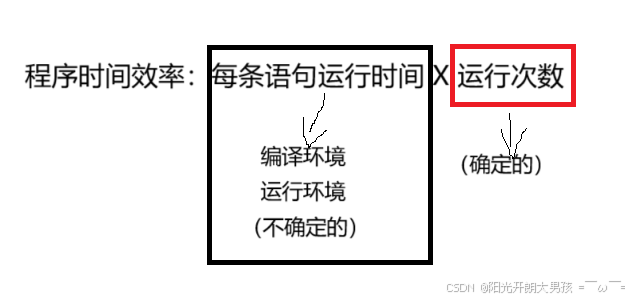
定义:在计算机科学中,算法的时间复杂度是⼀个函数式T(N),它定量描述了该算法的运⾏时间。时 间复杂度是衡量程序的时间效率,那么为什么不去计算程序的运⾏时间呢?
- 因为程序运⾏时间和编译环境和运⾏机器的配置都有关系,⽐如同⼀个算法程序,⽤⼀个⽼编译 器进⾏编译和新编译器编译,在同样机器下运⾏时间不同。
- 同⼀个算法程序,⽤⼀个⽼低配置机器和新⾼配置机器,运⾏时间也不同。
- 并且时间只能程序写好后测试,不能写程序前通过理论思想计算评估。
空间复杂度
空间复杂度也是⼀个数学表达式,是对⼀个算法在运⾏过程中因为算法的需要额外临时开辟的空间。 空间复杂度不是程序占⽤了多少bytes的空间,因为常规情况每个对象⼤⼩差异不会很⼤,所以空间复 杂度算的是变量的个数。
注意:函数运⾏时所需要的栈空间(存储参数、局部变量、⼀些寄存器信息等)在编译期间已经确定好 了,因 此空间复杂度主要通过函数在运⾏时候显式申请的额外空间来确定
⼤O的渐进表⽰法
我们只需要计算程序能代表增⻓量 级的⼤概执⾏次数,复杂度的表⽰通常使⽤⼤O的渐进表⽰法。
⼤O符号(Big O notation):是⽤于描述函数渐进⾏为的数学符号
计算时间复杂度
推导⼤O阶规则
注意:对计算机运行效率来说,执行次数亿、万、1并无差别
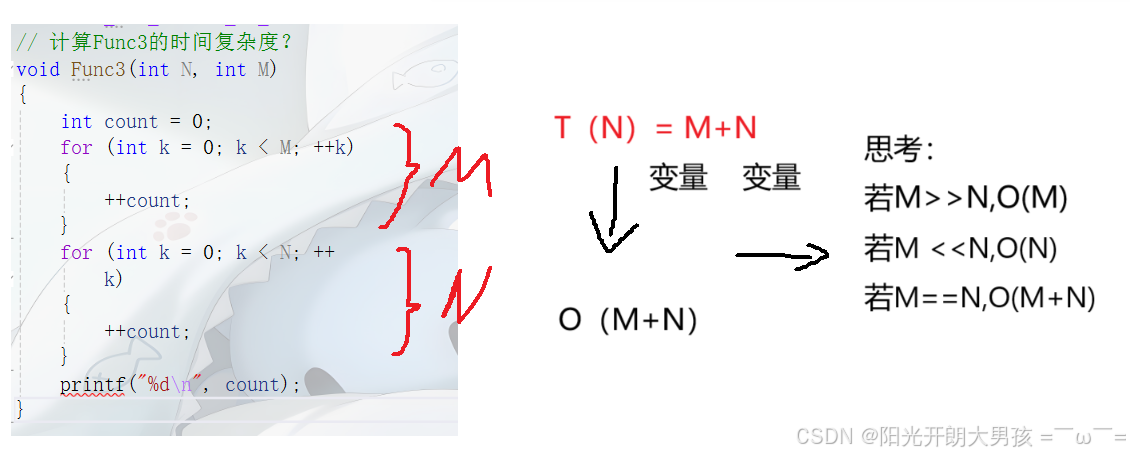
- 时间复杂度函数式T(N)中,只保留最⾼阶项,去掉那些低阶项,因为当N不断变⼤时, 低阶项对结果影响越来越⼩,当N⽆穷⼤时,就可以忽略不计了。示例:
- 如果最⾼阶项存在且不是1,则去除这个项⽬的常数系数,因为当N不断变⼤,这个系数 对结果影响越来越⼩,当N⽆穷⼤时,就可以忽略不计了。
- T(N)中如果没有N相关的项⽬,只有常数项,⽤常数1取代所有加法常数。
特殊情况
有些算法的时间复杂度存在最好、平均和最坏情况。
最坏情况:任意输⼊规模的最⼤运⾏次数(上界)
平均情况:任意输⼊规模的期望运⾏次数
最好情况:任意输⼊规模的最⼩运⾏次数(下界)
⼤O的渐进表⽰法在实际中⼀般情况关注的是算法的上界,也就是最坏运⾏情况。
冒泡排序的复杂度计算
注意!!!内循环有误:i = 1,应为n-1 n-2…….1 0共n个数
关于对数(log n)的复杂度
注意:
- 文章中 log2 n 、 log n 、 lg n 的表⽰
- 当n接近⽆穷⼤时,底数的⼤⼩对结果影响不⼤。
- 因此,⼀般情况下不管底数是多少都可以省略不 写,即可以表⽰为 log n 不同书籍的表⽰ ⽅式不同,以上写法差别不⼤,建议使⽤ log n
递归的时间复杂度
(单次递归的时间复杂度 * 递归次数)
计算空间复杂度
空间复杂度计算规则基本跟时间复杂度类似。
注意!!!:函数运⾏时所需要的栈空间(存储参数、局部变量、⼀些寄存器信息等)在编译期间已经确定好 了,因 此空间复杂度主要通过函数在运⾏时候显式申请的额外空间来确定
冒泡排序的空间复杂度
递归的空间复杂度
复杂度算法题(实战演练)
旋转数组
. – 力扣(LeetCode)
给定一个整数数组
nums,将数组中的元素向右轮转k个位置,其中k是非负数。输入: nums = [1,2,3,4,5,6,7], k = 3 输出:[5,6,7,1,2,3,4]解释: 向右轮转 1 步:[7,1,2,3,4,5,6]向右轮转 2 步:[6,7,1,2,3,4,5]向右轮转 3 步:[5,6,7,1,2,3,4]示例 2:
输入:nums = [-1,-100,3,99], k = 2 输出:[3,99,-1,-100] 解释: 向右轮转 1 步: [99,-1,-100,3] 向右轮转 2 步: [3,99,-1,-100]提示:
1 <= nums.length <= 105-231 <= nums[i] <= 231 - 10 <= k <= 105思路1
空间复杂度 O(1)
时间复杂度 O(n^2 )
循环K次将数组所有元素向后移动⼀位(代码不通过)
void rotate(int* nums, int numsSize, int k) { while(k--) { int end = nums[numsSize-1]; for(int i = numsSize - 1;i > 0 ;i--) { nums[i] = nums[i-1]; } nums[0] = end; } }
思路2:
空间复杂度 O(n)
时间复杂度 O(n )
申请新数组以空间换时间
申请新数组空间,先将后k个数据放到新数组中,再将剩下的数据挪到新数组中
void rotate(int* nums, int numsSize, int k) { int newArr[numsSize]; for (int i = 0; i < numsSize; ++i) { newArr[(i + k) % numsSize] = nums[i]; } for (int i = 0; i < numsSize; ++i) { nums[i] = newArr[i]; } }
思路3:(涉及双指针)
空间复杂度 O(1)
时间复杂度 O(n )
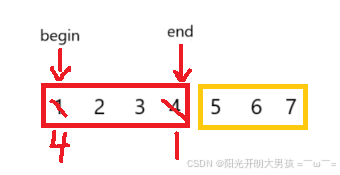
前n-k个逆置: 4 3 2 1 5 6 7
后k个逆置 :4 3 2 1 7 6 5
整体逆置 : 5 6 7 1 2 3 4
运行机制:
void reverse(int* nums,int begin,int end) { while(begin<end){ int tmp = nums[begin]; nums[begin] = nums[end]; nums[end] = tmp; begin++; end--; } } void rotate(int* nums, int numsSize, int k) { k = k%numsSize; reverse(nums,0,numsSize-k-1); reverse(nums,numsSize-k,numsSize-1); reverse(nums,0,numsSize-1); }
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/126960.html